Научный журнал

Научное обозрение. Технические науки

ISSN 2500-0799

ПИ №ФС77-57440

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бостанов Б.О. 1

---

1 РГП на ПХВ «Евразийский национальный университет им. Л.Н. Гумилева»

Рассмотрена задача об определении положения точек сопряжения комбинированной траектории, обеспечивающих условия касания, непрерывности и равенства радиуса кривизны. При сопряжении дуг круговой и эллиптической траектории в месте соединения, где имеется общая касательная, возникает скачок центробежной силы из-за неравенства радиусов кривизны, что приведет к удару. Для того чтобы не было скачка кривизны, применяется метод вставки сглаживающей кривой второго порядка (переходной коники). Известны способы непрерывного, гладкого соединения траекторий, к которым относятся обводы, сплайны. При таком сопряжении выполняются условия касания и непрерывности двух дуг кривых, но не выполняется условие равенства радиусов кривизны этих кривых в точке стыка. Было определено математическое условие безударного сопряжения траекторий. Задавая начальную точку соединения и используя условие плавности (гладкости второго порядка), можно определить конечную точку переходной кривой. Предлагается процесс моделировать кулисным механизмом, который позволяет наглядно, быстро и эффективно определить положение финишной точки на окружности. Используя основанный на кинематике кулисного механизма способ определения положения точек сопряжения, можно осуществить плавное соединение конических дуг, удовлетворяющих условиям непрерывности, касания и равенства кривизны, и создать на их основе новые модели беговых дорожек (траектории) из конических дуг, которые позволяют исключить нежелательные ударные эффекты.

Статья в формате PDF

0 KB

коника

радиус кривизны

плавность соединения

кулиса

кулисный камень

1. Муфтеев В.Г., Марданов А.Р. Изогеометрическое моделирование кривых линий и поверхностей высокого качества по базовым критериям плавности / Сборник трудов ДонНТУ серии «Информатика, кибернетика и вычислительная техника». – 2009. – Вып. 10(153). – С. 131–145.

2. Бостанов Б.О. Условия плавного сопряжения переходного участка / Б.О. Бостанов // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 2. – С. 164–167.

3. Тарг С.М. Краткий курс теоретической механики: учеб. для втузов. – 20-е изд., стер. – М.: Высш. шк., 2010. – 416 с.

4. Берг М., Чеонг О., Кревельд М., Овермарс М. Вычислительная геометрия. Алгоритмы и приложения = Computational Geometry: Algorithms and Applications. – М.: ДМК-Пресс, 2016. – 438 с.

5. Краткий справочник для инженеров и студентов: Высшая математика. Физика. Теоретическая механика. Сопротивление материалов / А.Д. Полянин и др. – М.: Международная программа образования, 2008. – 432 с.

Возрастающие требования безопасности и плавности движения, обтекаемости профилей объектов инициировали развитие теории переходных кривых и методов их проектирования. Разработка принципиально новых методов плавного соединения конических траекторий движущегося тела, в том числе на основании теории механизмов и машин, аналитической механики, проективной геометрии, синергетики и построении на этой основе новых сложных технических форм беговых дорожек (траектории) является одной из важнейших задач [1].

Цель исследования – определение положения точек сопряжения комбинированной траектории, состоящей из дуг конических сечений, для обеспечения безударного движения по ней.

Материалы и методы исследования

Для исследования рассматривается механико-математическая модель составной конической траектории, по которой движется материальная точка и методика аналитического исследования с применением аппарата аналитической, дифференциальной геометрии и теории механизмов машин.

Результаты исследования и их обсуждение

Рассмотрим некоторую комбинированную беговую дорожку (траекторию), состоящую из полудуг эллипса 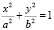и полудуг окружности 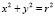, по которой движется тело (материальная точка) (рис. 1, а).

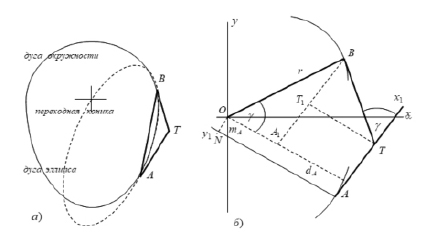
Рис. 1. Комбинированная беговая дорожка и точки сопряжения

Точка по комбинированной беговой дорожке совершает движение по дугам кривых различной кривизны. При переходе из одной части в другую в точках сопряжения возникает разрыв кривизны, вызывающий скачок центробежной силы. Для того, чтобы обеспечить переход без скачка, необходимо между ними вставить переходный участок в виде дуги кривой, удовлетворяющей условиям [2]:

а) дуга должна проходить через точки сопряжения А и B;

б) в точках сопряжения соединяющая и соединяемая части должны иметь одинаковую непрерывную первую производную (в этой точке скорости должны быть равными);

в) в точках сопряжения соединяющая и соединяемая части должны иметь одинаковую непрерывную вторую производную (в этой точке радиусы кривизны должны быть равными).

Кониками являются всякая невырожденная кривая второго порядка, которая получается как сечение конуса. Соединения, обеспечивающие все три вышеперечисленные условия, соответствуют гладкости второго порядка или плавности. Таким образом, плавным переходным участком, удовлетворяющим условиям касания, непрерывности и равенства радиусов кривизны, может быть любая коника (эллипс, парабола, гипербола), дуга которой лежит внутри базового треугольника ΔATB.

Пусть переходный участок определен в виде коники. Точка А будет общей точкой касания и для дуги эллипса, и для дуги коники (стартовая точка), прямая АT является их общей касательной, а также в этой точке А коника и эллипс имеют одинаковый радиус кривизны ρ_A. Аналогично, точка B – общая точка для дуг коники и окружности (финишная точка), BT – их общая касательная, проведенная через точку B и ρ_B – их радиус кривизны в этой точке B сопряжения.

Было установлено [1], чтобы переходная коника обеспечивала плавное соединение в точках сопряжения А и B, должно выполняться следующее математическое условие:

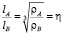, (1)

где 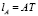– длина касательной AT, 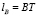– длина касательной BT.

Соотношение (1) указывает на то, что для построения плавной переходной коники, дуга которой находится внутри базового треугольника ΔATB, надо определить положение финишной точки B на окружности при заданной стартовой точке А.

Выберем на дуге заданного эллипса некоторую произвольную стартовую точку А с радиусом кривизны ρ_A и проводим через нее касательную. Стартовую точку А фиксируем как начало неподвижной системы координат Ax1y1. Ось Ax1 направим вдоль касательной AT к эллипсу в этой точке А, а ось Ay1 – вдоль нормали AN (рис. 1, б).

Так как мы имеем заданную окружность 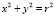, то любая точка B на окружности имеет радиус кривизны, равной радиусу самой окружности, т.е. ρ_B = r. Касательная BT, проведенная через точку B, пересекает касательную AT в точке T. Угол между касательными AT и BT обозначим через γ. Измененяя положение точки B на окружности, мы каждый раз проведем касательную к окружности из нового положения B, а это приведет к изменению положения точки пересечения T на оси Ax1, следовательно, меняется и угол γ. Таким образом, изменяя угол наклона γ касательной BT относительно неподвижной оси Ax1 мы можем найти положение точки B на окружности. Угол наклона γ должен обеспечивать выполнение соотношения вида (1), т.е. отношение длин отрезков касательных, проведенных из точек соединения А и B, равно относительному показателю кривизны η.

Предлагается процесс определения положения точки B с условием выполнения соотношения 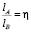моделировать кулисным механизмом [3].

Используя рис. 1, б и основываясь на задания вида траектории, построим кинематическую схему кулисного механизма. Если предположить, что окружность радиуса r является круговой траекторией точки B, то стержень OB = r вращается вокруг оси, проходящей через точку O. Так как касательная к окружности всегда перпендикулярна радиусу, то стержни OB и BT, направленные по касательным и нормали к окружности в точке B и жестко соединенные между собой под прямым углом в точке B, создают вращательное звено механизма (рис. 2).

Снабдим стержень BT прямолинейной прорезью, в которой перемещается небольшой ползун T – кулисный камень, тогда стержни OB и BT образуют кулису OBT. Ползун T – кулисный камень представляет точку пересечения касательных AT и BT. Вдоль линии AT расположим поступательно перемещающийся стержень Tx1. Камень кулисы T перемещается в прорези BT и шарнирно соединен в точке T со стержнем Tx1, которая направлена вдоль касательной к эллипсу в точке A.

Таким образом, мы получили кулисный механизм, в котором кулиса OBT, вращаясь в плоскости Ax1y1 вокруг неподвижной оси, проходящей через точку O, приводит в движение камень T. Камень T, скользя в прорези BE, в свою очередь приводит в поступательное движение стержнь Tx1 вдоль оси Ax1.

Следовательно, камень T во время движения остается в пересечении направляющих BT и Tx1. При таком движении кулисного камня T кулисного механизма происходит одновременное изменение расстояний от точек сопряжения А и B до точки пересечения касательных, т.е. изменения длин касательных AT и BT.

Определяя уравнение движения камня T, можно обеспечить выполнение соотношения .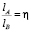

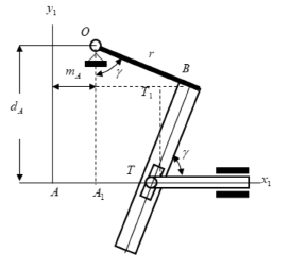
Рис. 2. Кулисный механизм

Полученный кулисный механизм имеет одну степень свободы, и пусть γ – угол поворота прямоугольной кулисы OBT вокруг неподвижной оси, проходящей через точку O, отсчитываемый от линий OA1.

Угол γ также определяет положение стержня BT кулисы относительно неподвижного направления Ax1. Обозначим через dA и mA расстояния от неподвижного шарнира O до направляющей Ax1 и нормали Ay1 соответственно.

Найдем координаты точек T и B как функции угла γ (рис. 2) [4–5].

Для точки T:

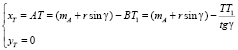
или

.

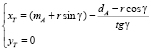Для точки B:

.

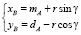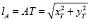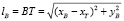Учитывая, что длины касательных и , а также выражая тригонометрические функции 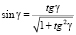, , 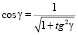найдем изменение длин как функцию угла поворота γ кулисы:

,

.

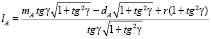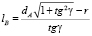Таким образом, с учетом соотношения (1) получаем уравнение относительно :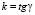

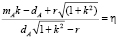. (2)

Уравнение (2) можно решить графически, т.е. решение можно получить как точку пересечения графиков

.

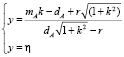Решение 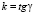представляет собой угловой коэффициент искомой касательной BT. Точка B находится как точка касания окружности 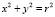и касательной BT: .

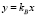Предлагается другой вариант нахождения координаты точки B, если угловой коэффициент искомой касательной BT уже определен. Пусть kAn – угловой коэффициент нормали Ay1, k – угловой коэффициент касательной BT, а kBn – угловой коэффициент нормали OB. Тогда .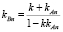

Рис. 3. Построения для определения финишной точки

Пересечение прямой 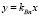с окружностью 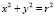определяет финишную точку B:

.

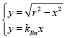Пример. Пусть нам дана комбинированная траектория, состоящая из полудуг окружности 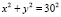и эллипса 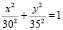. Чтобы в точках (–30; 0) и (30; 0) не было скачка кривизны, между дугами двух кривых нужно вставить переходную конику. Для этого выберем на эллиптической дуге некоторую стартовую точку A(24; –21), где ρ_A = 35,1253. Тогда η = 1,054. Вычислим необходимые величины и изобразим на рис. 3.

: ,

, ,

;

: ,

, ,

.

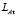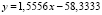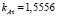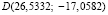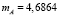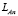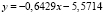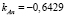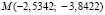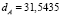Тогда

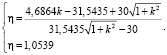
По найденному решению k = 0,9291 вычислим угловой коэффициент нормали к окружности, т.е. kBn = 0,1791. Следовательно, пересечение окружности с нормалью

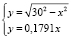
определяет положение финишной точки B(29,5301; 5,2888).

Производим проверку. T(32; –8,5425) – точка пересечения касательных, проведенных через точки A и B. Тогда AT = 14,51, BT = 14,5, следовательно, .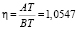

Заключение

При выполнении условий плавности сопряжения можно осуществить вставку переходной кривой, дуга которой находится внутри базисного треугольника с точками соединения и пересечения касательных. Применяя способ определения положения начальных и конечных точек соединения на основе кинематики кулисного механизма, можно осуществить плавное соединение конических дуг, удовлетворяющих условиям непрерывности, касания и равенства кривизны, и создать на их основе новые модели траектории из конических дуг, которые позволяют исключить нежелательные скачкообразные эффекты.

Библиографическая ссылка