Если наблюдателю предложить белый, черный и группу серых образцов цветов и, попросить его выбрать из них такой, который в равной степени отличается и от белого, и от черного, он столкнется с небольшой трудностью, поскольку оценка относительной величины двух больших цветовых различий, в конечном счете, основана только на субъективном впечатлении. Это является частным случаем определения цветовых различий, который Ньюхолл назвал методом отношений цветовых различий [1]; в данном случае отношение составляет 1:1. Однако нужный серый цвет можно определить, исходя из усредненной оценки нескольких наблюдателей, причем желаемая точность зависит только от количества наблюдателей и числа сделанных ими оценок. Затем цветовой интервал, находящийся между черным и средне-серым можно поделить пополам, аналогично можно поступить с интервалом – между белым и средне-серым цветами. Таким образом, диапазон от черного до белого образует равноконтрастную шкалу светлоты, состоящую из пяти равноудаленных по субъективному ощущению цветов. Это был один из методов, используемых для определения шкалы серых цветов по Манселлу [2, 3].
Другой метод создания равноконтрастной шкалы светлоты (начиная с черного цвета) состоит в выборе чуть более светлого серого цвета, затем чуть более светлого, чем этот выбранный цвет, и так до тех пор, пока мы не подойдем к белому или близкому к белому цвету.
Эти же два метода могут использоваться для установления равноконтрастной шкалы светлоты в интервале от любого светлого до любого темного цветов, при условии наличия образцов промежуточных цветов, незначительно отличающихся друг от друга.
Большой интерес вызывает метод преобразование цветового локуса, предложенный в [4, 5].
Постановка задачи
В начале 40 годов прошлого столетия появились публикации результатов опытов, проведенных Мак-Адамом по выяснению порогов цветоразличения [6-10]. Аналогичные опыты были также проведены Стайлсом [11], Вышецки [12], а также повторно самим Мак-Адамом. Их результаты в целом согласовывались с результатами, полученными изначально Мак-Адамом и графически отображались в виде эллипсов на цветовой диаграмме МКО 1931 г. (x, y). На рис. 1. изображены результаты опытов Мак-Адама, которые впоследствии получили название «Эллипсы Мак-Адама».
Из рис. 1 можно сделать весьма интересное заключение. Поскольку в пределах любого эллипса глаз наблюдателя не видит цветового различия, то с точки зрения глаза эллипс представляет собой точку, с координатами на цветовой диаграмме МКО, определяемой координатами любой из точек эллипса. Но если измерять координаты цветности с помощью высокоточного прибора в пределах области эллипса, мы получим конкретные цветности для каждой точки внутри области, ограниченной эллипсом Мак-Адама. Отсюда следует, что с точки зрения глаза наблюдателя эллипсы Мак-Адама не имеют центра.
Автором был разработан программный комплекс по измерению порогов цветоразличения [13, 14], описание которого дано в [15, 16]. Впоследствии этот программный комплекс был изменен. Суть этого изменения заключалась в том, что пороги цветоразличения определялись в зависимости от яркости излучения сравниваемых цветов (яркости стимула в процентном соотношении). На рис. 2 (нижняя часть рисунка) показаны результаты эксперимента (рисунок имеет иллюстративный характер). Экстраполируя кривую зависимости величины порога до значения яркости равной нулю, получим величину порога равную бесконечности, а точнее порог, ограниченный кривой цветового локуса. Известно, что при уменьшении яркости включается механизм ночного или сумрачного зрения, т.е. в процесс зрения включаются палочки глаза, а колбочки выключаются, как имеющие цветочувствительность в отличие от палочек. Имеет место эффект Пуркинье («ночью все кошки серые»).
Очевидно, что при увеличении яркости излучения до очень больших значений, цветочувствительность глаза также будет уменьшаться. Это явление можно объяснить тем, что распад йодопсина (светочувствительное вещество колбочек глаза) будет происходить быстрее, нежели его восстановление. Глаз станет цветослепым, т.е. величина порога цветоразличения будет увеличиваться по мере увеличения яркости излучения и, при очень больших яркостях порог цветоразличения будет равен бесконечности, точнее эта бесконечность будет ограничена цветовым локусом. Конечно, такая яркость в природе, а тем более в телевидении (на экране монитора), не реализуется и может быть рассмотрена только теоретически. Графически это можно представить так, как это показано на рис. 2 (верхняя часть рисунка).
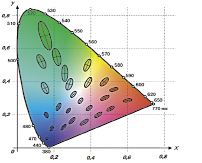
Рис. 1. Эллипсы Мак-Адама (для наглядности размеры эллипсов увеличены в 10 раз)
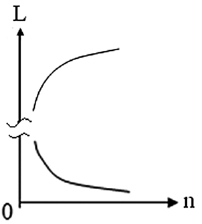
Рис. 2. Зависимость величины порога цветоразличения n от яркости L
Цветовое пространство
Посмотрим на картину в целом (рис. 3). На этом рисунке изображен однополостный гиперболоид [17]. Прежде чем рассуждать далее, необходимо ввести некоторые обозначения:
1. Горизонт цвета (аналогично «горизонт событий в обшей теории относительности (ОТО)) – под этим здесь будем понимать некий объем, в котором, с точки зрения цветоразличения глаза, цвет однородный;
2. Бесконечность – область, ограниченная цветовым локусом;
Рассмотрим некоторые области этого гиперболоида. О верхней и нижней частях рисунка, окрашенных соответственно в белый и черный цвета, можно сказать, что горизонт событий уходит в бесконечность. Сами эти поверхности линейны, плоские и имеют евклидовую геометрию. Более сложную структуру имеет пространство, расположенное в центральной части рисунка.
Горизонт цвета имеет малый радиус, а это обстоятельство указывает, что пространство, заключенное под горизонтом цвета, искривлено и замкнуто, аналогично, как это имеет место в пространстве черных дыр в фундаментальной теории эволюции звезд. В связи с этим можно для решения вопросов порогов цветовосприятия, а также для создания новых равноконтрастных цветовых систем, в которых бы все эллипсы Мак-Адама трансформировались в одинаковые окружности, а в трехмерном пространстве – в шары равного диаметра, можно использовать уравнение Эйнштейна [18 - 21].
Иногда встречается название — уравнения гравитационного поля в общей теории относительности (ОТО), связывающие между собой метрику искривлённого пространства-времени со свойствами заполняющей его материи. Этот термин используется и в единственном числе: «уравнение Эйнштейна», так как в тензорной записи это одно уравнение, хотя в компонентах оно представляет собой систему уравнений.
Выглядят уравнения следующим образом [16 - 18]:
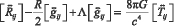 (1)
(1)
или
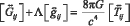
где 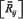 — тензор Риччи, получающийся из тензора кривизны пространства-времени
— тензор Риччи, получающийся из тензора кривизны пространства-времени 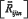 посредством свёртки его по паре индексов, R — скалярная кривизна, то есть свёрнутый тензор Риччи,
посредством свёртки его по паре индексов, R — скалярная кривизна, то есть свёрнутый тензор Риччи, 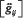 — метрический тензор, Λ — космологическая постоянная, а
— метрический тензор, Λ — космологическая постоянная, а  представляет собой тензор энергии-импульса материи, (с — скорость света в вакууме, G — гравитационная постоянная),
представляет собой тензор энергии-импульса материи, (с — скорость света в вакууме, G — гравитационная постоянная), 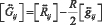 - тензор А. Эйнштейна. Так как все входящие в уравнения тензоры симметричны, то в четырёхмерном пространстве-времени эти уравнения равносильны скалярным уравнениям.
- тензор А. Эйнштейна. Так как все входящие в уравнения тензоры симметричны, то в четырёхмерном пространстве-времени эти уравнения равносильны скалярным уравнениям.
Уравнения Эйнштейна не налагают никаких ограничений на используемые для описания пространства-времени координаты, то есть обладают свойством общей ковариантности, и они ограничивают выбор лишь 6 из 10 независимых компонент симметричного метрического тензора. Поэтому их решение неоднозначно без введения некоторых ограничений на компоненты метрики, соответствующих однозначному заданию координат в рассматриваемой области пространства-времени, и называемых, поэтому обычно координатными условиями [19 - 21]. Решая уравнения Эйнштейна совместно с правильно подобранными координатными условиями, можно найти все 10 независимых компонент симметричного метрического тензора. Этот метрический тензор (метрика) описывает свойства пространства-времени в данной точке и используется для описания результатов физических экспериментов.
Он позволяет задать квадрат интервала в искривлённом пространстве:
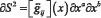 (2)
(2)
который определяет «расстояние» в физическом (метрическом) пространстве.
Рассмотрим в отдельности составляющие уравнения (1). Это уравнение предполагает четырехмерное пространство-время, поэтому будем рассматривать его компоненты в четырехмерном пространстве. Согласно [22], в так называемых Шварцшильдовских координатах из которых 3 последних аналогичны сферическим, наиболее физически важной части пространства-времени Шварцшильда с топологией R2xS2 (произведение области двухмерного евклидова пространства и двумерной сферы), имеет вид:
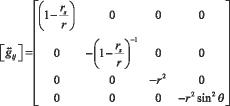
где rs= rg – радиус Шварцшильда, равный гравитационному радиусу.
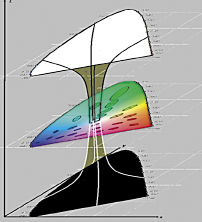
Рис. 3. Зависимость порогов цветоразличения от яркости излучения
Интервал в этой метрике записывается как:
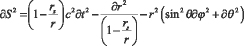
На рис. 4 приведена графическая интерпретация пространства Шварцшильдом.
Следующим компонентом уравнения (1) – является тензор энергии- импульса. Симметричный тензор энергии-импульса, определенный в пространстве-времени, который одновременно задает плотность энергии и ее потоков и определяет закон изменения этих величин при переходе от одной системы отчета в другую.
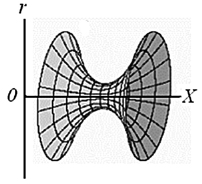
Рис. 4. Графическая интерпретация решения Шварцшильда
Тензор энергии-импульса в общем случае имеет вид [23]:
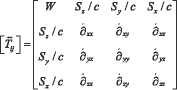 (3)
(3)
где W - плотность энергии; Si – поток энергии в направлении, задаваемом
д?tv=ρvtvv+δtv , t,v=x,y,z.
О тензоре кривизны пространства, тензоре Риччи  поговорим позже.
поговорим позже.
Космологическая постоянная или энергия вакуума Λ в нашем случае будет равна нулю.
Итак, разобрано уравнение (1), причем все составляющие (кроме тензора Риччи) рассмотрены в матричной форме.
Для применения уравнения (1) для преобразования цветового пространства в строго равноконтрастное цветовое пространство поступим следующим образом. Обычно в телевидении для оценки цвета применяют колориметрическую систему МКО 1960 г. (u,v, w), но не исключается применение колориметрической системы МКО 1931 г.(x,y,z). Мы остановимся на первой системе (МКО 1960 г. (u,v, w)). В этой системе среднее значение порога цветоразличения равно 0,0038. Будем считать, что эта система цветности – трехмерна и имеет взаимно перпендикулярные оси u,v, w. Это обычное трехмерное метрическое пространство на поверхности цветового пространства выбранной колориметрической системы. И эта метрика, в принципе, ни чем не отличается от метрики окружающего пространства, за исключением - единиц измерения. В качестве четвертого измерения в нашем цветовом пространстве используем яркость излучения света. Отметим, что каждой точке цвета на цветовом локусе [24] соответствует своя яркость. Известно, что яркость белого цвета, в частности в телевидении, является максимальной яркостью. В наших преобразованиях необходимо пронормировать яркость любой точки на цветовом локусе относительно белого цвета.
Поскольку динамический диапазон яркости, воспринимаемый человеческим глазом, составляет примерно семь порядков — условно говоря, от 1 до 10 млн. единиц. Чтобы получить представление лишь о части этого диапазона, можно отметить, что контраст между ярким солнечным днем и темной безлунной ночью составляет около одного миллиона к единице. Для восприятия такого большого динамического диапазона яркостей у нашего глаза характеристика свет-сигнал подчиняется логарифмическому закону. Поэтому после приведения яркости заданной точки на цветовом локусе к яркости белого, ее необходимо пересчитать, например, как это делается в системе МКО 1976 г. В этой формуле координата цвета пропорциональна яркости, так как кривая видности глаза полностью совпадает с кривой сложения цвета ?(λ) колориметрической системы МКО 1931 г. (x, y, z).
Таким образом, мы подготовили четырехмерное цветовое пространство, и осталось рассмотреть тензор кривизны – тензор Риччи.
Кривизна пространства цветоразличения
Выше была рассмотрена структура правой части уравнения (1). Но в уравнение Эйнштейна входит тензор кривизны – тензор Риччи. Рассмотрим структуру данного тензора. Как известно [25] тензор Риччи был получен из классического тензора кривизны путем его свертки, согласно:
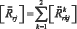 (4)
(4)
где  - тензор Риччи,
- тензор Риччи, 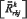 - тензор кривизны.
- тензор кривизны.
Формулу (4) для тензора Риччи можно преобразовать к следующему виду:
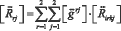 (5)
(5)
Из тензора Риччи можно построить скаляр R по следующей формуле:
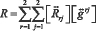 (6)
(6)
Скаляр R(x1,x2) определенный (4.6) – есть скалярная кривизна пространства поверхности в точке с координатами x1,x2. Скалярная кривизна - это полная свертка тензора кривизны R:
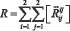 (7)
(7)
Переход от компонент тензора 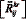 к скалярной кривизне R – это на первый взгляд потеря информации, т.е. девять величин заменяются одной. Однако в двумерном случае никакой потери информации не происходит. Действительно компоненты тензора кривизны
к скалярной кривизне R – это на первый взгляд потеря информации, т.е. девять величин заменяются одной. Однако в двумерном случае никакой потери информации не происходит. Действительно компоненты тензора кривизны  кососимметричны как по верхней паре индексов, так и по нижней паре индексов. При совпадении k=r или i=j, они зануляются. Единственные ненулевые компоненты – это
кососимметричны как по верхней паре индексов, так и по нижней паре индексов. При совпадении k=r или i=j, они зануляются. Единственные ненулевые компоненты – это 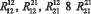 , причем
, причем  .Тогда, в силу сказанного, получаем:
.Тогда, в силу сказанного, получаем:
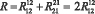 (8)
(8)
Рассмотрим рис. 5 [26]. Проведем плоскость P касательную к поверхности сферы. Через точку M касания перпендикулярно этой плоскости рассечем поверхность двумя взаимно перпендикулярными плоскостями N1 и N2. На поверхности образуются две пересекающие в точке M кривые A1MB1 и A2MB2. Тогда средняя кривизна поверхности в точке М есть величина:
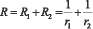 (9)
(9)
где R1 – радиус кривизны и кривизна первой кривой в точке M; R2 - тоже самое, но для второй кривой.
В случае сферической поверхности r1=r2=r0 имеем:
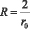 (10)
(10)
Таким образом, были окончательно получены все компоненты уравнения (1). Но перед тем как решать это уравнение, необходимо определить и конкретизировать тензор энергии-импульса, что и будет сделано в следующем подразделе.
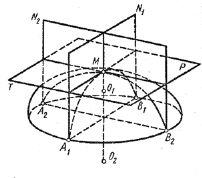
Рис.5. Кривизна поверхности
Тензор энергии-импульса цвета
Перепишем тензор энергии-импульса (3) [22]:
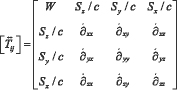 (11)
(11)
Что бы не путать этот тензор, введем новое обозначение с новыми компонентами, при этом физический смысл нового тензора энергии-импульса цвета не должен отличаться от тензора энергии-импульса.
Обозначим этот тензор энергии-импульса цвета 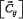 . Для обозначения новых компонент этого тензора, обратимся к рис. 6.
. Для обозначения новых компонент этого тензора, обратимся к рис. 6.
В (11) существует плотность энергии W. Очевидно, эта плотность энергии будет соответствовать значению плотности яркости эллипса Мак Адама. Согласно определению Мак Адама данный эллипс, а с учетом яркости - будет эллипсоид, является порогом цветоразличения и яркости. Значит, с точки зрения глаза, данный эллипсоид будет восприниматься как геометрическая точка, никаких цветовых, так и яркостных различий по области (и внутри тоже) не будет. Поэтому плотность световой энергии будет равна яркости точки, например центра эллипса (рис. 6). Поскольку эти эллипсы Мак Адам получил в своих опытах (измеряя координаты цвета) еще в первой половине прошлого столетия, и фактически в наше время достаточно трудно повторить эти опыты, то была разработана специальная программа, позволяющая по изображению эллипсов на цветовом локусе определять координаты любой точки и ее яркость.
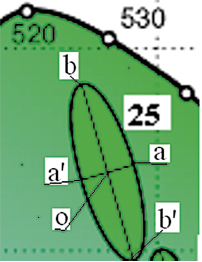
Рис. 6. Отдельно взятый эллипс Мак-Адама
Несколько слов о яркостях точек эллипсов Мак-Адама. Для определения яркости указанных точек поступим следующим образом. Предположим, что цветность каждой точки эллипса создаются с помощью монохромных излучателей (два спектральных цвета). При вычислении яркости спектральных цветов можно поступить следующим образом [27]. Взяв кривую видности глаза (рис. 7), можно в соответствии с длиной волны спектрального цвета цветового локуса определить относительную величину ощущения яркости по этой кривой.
Для не спектральных цветов цветового локуса, например, для цветов эллипсов Мак-Адама, а также для построения сетки на локусе, данный метод не может быть использован, так как насыщенность цвета внутри области локуса уменьшается.
Для преобразования плоского двухмерного цветового пространства x, y системы МКО 1931 г. была разработана специальная компьютерная программа, которая позволяет снять координаты любой точки экрана (в координатах экрана) и произвести запись координат в базу данных.
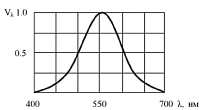
Рис.7. Кривая видности глаза
Согласно закона Вебера-Фехнера, порог различения по яркости составляет 0,01 от текущей яркости [26]. Таким образом, были определены все координатные данные эллипсов. В этих «измерениях» была использована колориметрическая цветовая система МКО 1931 г. (x, y), без третьей координаты, но так как известно, что x+y+z=1, то, третью координату z легко вычислить. Для преобразования полученных координат из МКО 1931 г.(x, y,z) в координаты МКО 1960 г. (u, v, w) использовались известные формулы, при этом w=1–u–v.
Значения Sx, Sy и Sz в (11) будет определяться яркостью в точках a, b и d (на рис. 6 эта точка совпадает с точкой О, но лежит на оси перпендикулярной плоскости рисунка). Расстояние от точки O до точки d равно 0,01 значения яркости в точке О. дij – тензор напряжений, тензор в обычном трехмерном пространстве второго ранга, состоящий из девяти величин, представляющих для нашего случая изменения яркости в этих точках, относительно яркости центра эллипсоида, отнесенные к его площади поверхности.
Площадь поверхности эллипсоида определяется [17]:
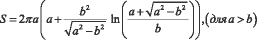
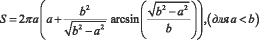
где a, b и d – полуоси эллипсоида. Перепишем полученный тензор энергии-импульса цвета:
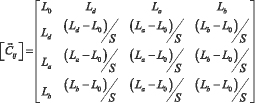 (12)
(12)
Перепишем метрический тензор, в соответствии с нашими данными:
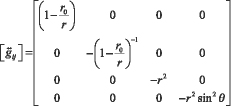
где r0=0,0038/2, 0,0038 – величина порога цветоразличения; r – радиус сферы цветового тела; θ – зенитный угол от начало координат, расположенных в центре цветового тела, в направлении центра эллипсоида.
Радиус сферы цветового тела зависит от величины яркости и для современных экранов телевизионных приемников может достигать значения 9000. Эта число равно динамическому диапазону по яркости, воспроизводимой на экране телеприемника. У современных экранов динамический диапазон может доходить до 9000 (1:9000).
Решение уравнения
Выше были описаны все компоненты уравнения (1). Тогда согласно этому, запишем уравнение, которое и требуется решить, при этом заменим ранее определенные величины их значениями:
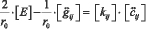 (13)
(13)
где 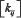 диагональная матрица констант, пропорциональных коэффициентам «подвижности» репера, в базисе подвижного репера в пространстве геометрии Римана; [E] единичная диагональная матрица, размерностью 4х4. При численном решении (13) нам и надо определить эту константу. Из-за ограничения объема статьи, опустим математические выводы и запишем конечное уравнение. При этом цветовое различие двух цветов Ц1 и Ц2, имеющие отличные яркости находятся на разных концентрических сферах, радиус которых однозначно определяется яркостью цвета (рис. 8).
диагональная матрица констант, пропорциональных коэффициентам «подвижности» репера, в базисе подвижного репера в пространстве геометрии Римана; [E] единичная диагональная матрица, размерностью 4х4. При численном решении (13) нам и надо определить эту константу. Из-за ограничения объема статьи, опустим математические выводы и запишем конечное уравнение. При этом цветовое различие двух цветов Ц1 и Ц2, имеющие отличные яркости находятся на разных концентрических сферах, радиус которых однозначно определяется яркостью цвета (рис. 8).
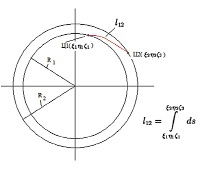
Рис. 8. Определение цветового различия двух цветов Ц1 и Ц2, имеющих отличные яркости и находящиеся на разных сферических поверностях, радиус которых однозначно определяется яркостью цвета
На рис. 9 длина вектора 0S отображает цветовую насыщенность центра эллипса Мак-Адама, а угол φ – цветовой тон.
Поскольку все вектора типа 0S (рис. 9) начинаются из нулевой точки, то длина этих векторов (цветовая насыщенность) определяется простым выражением типа: 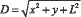 где x, y - координаты конца вектора в системе координат x’, y’, L – приведенная яркость точки конца вектора.
где x, y - координаты конца вектора в системе координат x’, y’, L – приведенная яркость точки конца вектора.
Итак, окончательное уравнение метрического тензора, который необходимо решить имеет вид:
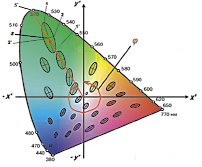
Рис. 9. Пороги Мак-Адама в системе координат x’ y’
где 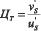 цветовой тон;
цветовой тон; 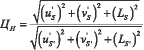 цветовая насыщенность; индексы S и S’ имеют значения, изображенные на рис. 9;
цветовая насыщенность; индексы S и S’ имеют значения, изображенные на рис. 9;
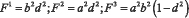
где a, b и d – полуоси эллипсоида; 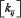 диагональная матрица констант, равная коэффициентам «подвижности» репера в базисе подвижного репера и пространстве геометрии Римана (искомые величины); [E] единичная диагональная матрица.
диагональная матрица констант, равная коэффициентам «подвижности» репера в базисе подвижного репера и пространстве геометрии Римана (искомые величины); [E] единичная диагональная матрица.
Из (14) получаем систему уравнений относительно  :
:
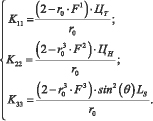 (15)
(15)
На рис. 10 и 11 приведены результаты решения (14) с учетом изложенного математического аппарата. Это решение было выполнено для колориметрической системы МКО 1931 г. (x’,y’).
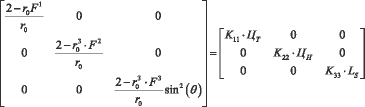 (14)
(14)
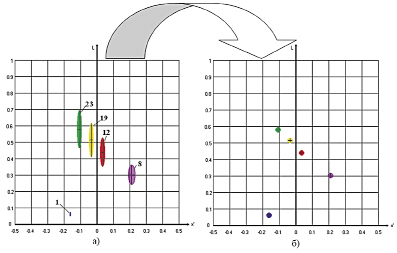
Рис.10. Сечение эллипсоидов плоскостью x’0L (a) и их пребразование в равновеликие шары (сечение той же плоскостью б). Размер эллипсоидов и шаров увеличен в 10 раз
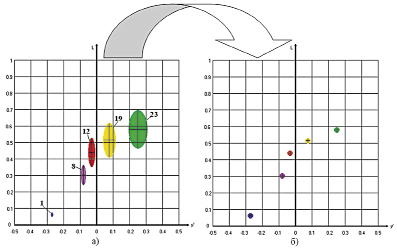
Рис. 11. Сечение эллипсоидов плоскостью y’0L (a) и их пребразование в равновеликие шары (сечение той же плоскостью б). Размер эллипсоидов и шаров увеличен в 10 раз
Очевидно, применяя вышеуказанную методику, можно пребразовать цветовое пространство (цветовой локус) в пространстве Римана. Так, например, если изобразить сферу, радиус которой равен величине максимальной яркости (яркость «белого» цвета) для системы МКО 1931г. (x’y’), а на поверхность этой сферы нанести цветовой локус, причем сохраняя переход от метрического плоского пространства к пространству Риммана, используя при этом базис пожвижного репера, то получим криволинейное цветовое пространство, на котором можно изобразить в этом же базисе подвижного репера пространства цветоразличения (шары Мак Адама).
Вышесказанное иллюстрирует рис. 12. На этом рисунке ось яркости перпендикулярна плоскости рисунка.
При данном математическом аппарате исходные данные могут быть представлены в любой из существующих колориметрических систем МКО, будь то МКО 1960 г. (u,v). Также можно получить результаты в колориметрический системе МКО 1976 г. (Lab) [28 -30].
Кроме того, данный математический аппарат дает возможность для обратного преобразования, при этом используется матрица обратного преобразования.
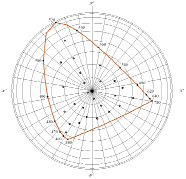
Рис. 12. Цветовой локус с эллипсами Мак-Адама в пространстве геометрии Римана. в системе МКО 1931 г.( x’y’)
Заключение
В заключение приведем основные выводы.
Обнаружено внешнее сходство между состоянием пространства-времени и цветовым пространством.
На основании этого сходства для разработки абсолютно равноконтрастного цветового пространства было применено уравнение А. Эйнштейна.
Решение данного уравнения производилось в стандартном четырехмерном пространстве, в котором использовалось трехмерное метрическое пространство uvw (системы МКО 1960 г.) и четвертое измерение – яркость, это позволило создать строго равноконтрастное четырехмерное цветовое пространство. Аналогично был произведен расчет и для трехмерного цветового пространства.
В качестве исходного цветового пространства можно использовать любое из известных цветовых пространств, и на выходе будут получены равные сферы порогов цветоразличения.
Полученное цветовое тело представляет собой сферу, радиус которой зависит от конкретной точки, изображающей цвет.
Цветовая разница между двумя цветами в полученной строго равноконтрастной цветовой системе определяется, как длина дуги, связывающей два цвета, лежащих на различных поверхностях концентрических сферах.
Применение разработанной строго равноконтрастной колориметрической системы в телевидении позволяет, при яркости изображения меньше пороговой чувствительности колбочек глаза, не передавать сигналы цветности, так как глаз человека не способен воспринимать при этом цвет. Это явление позволяет уменьшить информационную нагрузку на канал связи.
Разработанная методика позволяет осуществлять обратные преобразования к исходному цветовому пространству.


 science-review.ru
science-review.ru