Трудно назвать раздел гидравлики, в котором так же тщательно теоретически и экспериментально изучались турбулентные течения жидкости учеными самых различных стран и широкого спектра их ранга (от выдающихся теоретиков и экспериментаторов до аспирантов) и специализации (гидромеханики, физики, химики, почвоведы и т.д.).
Теория турбулентных течений жидкости крайне сложна. Непрерывные попытки преодолеть комплексный барьер из самых неожиданных трудностей при их изучении, предпринимаемые во всем мире, обозначаются некоторыми подвижками, к сожалению, развивающимися достаточно медленно. К еще большему сожалению можно отнести тот факт, что анализ даже самых простейших из практически значимых случаев турбулентных течений жидкости, например, расчёт распределения осреднённых скоростей в продольно – однородных течениях, до последнего времени не был доведен до необходимых кондиций. Эта проблема, с одной стороны, чрезвычайно важна в практическом отношении из-за широкой распространенности и использования во многих отраслях техники. С другой стороны, указанные течения часто используются в качестве своеобразного оселка для быстрой проверки и разработки новых научных идей, их уточнения и оттачивания до совершенства. Предполагается, что с использованием любопытных гипотез решение рассматриваемой задачи получило надёжную реализацию, что также включено в обзор.
1. У истоков возникновения проблемы распределения осреднённых скоростей в простейших канонических течениях жидкости
Как правило, исследователи, изучая закономерности потерь на трение в каналах и трубах, пытались, насколько это было возможным, решить и вторую, более сложную, задачу о распределении осреднённых скоростей в тех же потоках.
Исследования распределения скоростей в каналах производились намного раньше, чем в трубах. Первоначально с этой целью использовались простейшие измерительные средства, – поплавки. Но уже в 1732 г. Пито предложил изобретённую им трубку (трубку Пито) Парижской академии, а в 1790 г. В. Вольтман [28] описал гидрометрическую вертушку. Эти гидрометрические средства в усовершенствованном виде применяются до сих пор. В начальный период обработки экспериментальных данных было предложено значительное число ошибочных представлений о распределении осреднённых скоростей, были, в частности, предложены почти линейные, параболические с вертикальной и горизонтальной осью, эллиптические и т.п. эпюры их распределения. Лишь Пито с помощью поверхностных и глубинных поплавков доказал, что максимальная скорость на вертикали находится несколько ниже свободной поверхности, а затем скорости уменьшаются ко дну. Описание этих работ можно найти в [28].
Пожалуй, наибольшие достижения были получены Х. Дарси, начавшем исследования в 1855 г. [42]. После его смерти с 1858 по 1860 гг. его исследования продолжил Х. Базен [36], который до того был сотрудником Х. Дарси. Х. Дарси усовершенствовал трубку Пито и по результатам измерения с её помощью скоростей построил кривые, соединяющие точки с одинаковыми скоростями в живом сечении, – изотахи.
Этот прием наглядно показал значительное влияние боковых стенок на уменьшение скорости, которое сокращается по мере удаления от них. Базен установил, что если ширина потока более чем в пять раз превышает его глубину, то распределение скоростей по глубине на осевой вертикали, практически, совпадает с распределением скоростей в бесконечно широком прямоугольном канале. Заметим, что этот критерий в несколько уточненном виде используется до сих пор при измерениях в плоских потоках. Формулы Дарси и Базена имеют вид:
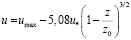 – Х. Дарси;
– Х. Дарси;
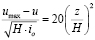 – Х. Базена,
– Х. Базена,
где H – глубина потока; z – расстояние от дна по вертикали; io – уклон дна.
Х. Базен проводил опыты в лотках шириной 2 м и длиной в несколько десятков метров на открытом воздухе, в том числе и в ветреную погоду при различном направлении ветра, причем скорость ветра намного превышала скорость воды. Он пришел к выводу, что влияние трения о воздух ничтожно мало.
И. Ясмунд [28] впервые, используя метод аппроксимаций, получил логарифмический закон распределения скоростей по вертикали.
Постепенно накапливались данные о пульсационных скоростях. С помощью измерений вертушкой Вольтмана было установлено, что пульсации имеют наименьшее значение у свободной поверхности и увеличиваются на вертикали ко дну, а по ширине – от фарватера к берегу .
Исследований распределения осреднённых скоростей в трубах также выполнено значительное количество. Сводка предлагавшихся эмпирических формул содержится в [12]. Рассмотрим лишь некоторые из полученных результатов.
Экспериментальные изучения распределения скоростей в трубах (из-за их сложности) начались позже, как уже отмечалось, чем в каналах. Сначала для труб малых диаметров (волосных трубочек) был получен теоретический закон распределения скоростей Пуазейля. В начальных опытах Базен установил, что скорость имеет максимум на оси трубы, но распределяется не по квадратичной, а по кубической параболе. Затем он этот закон заменил «квадратом эллипса». Из этой зависимости следовало, что [28]
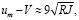 (1.1)
(1.1)
а радиус, на котором скорости равны средней скорости
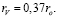 (1.2)
(1.2)
Соотношение средней и максимальной скоростей оказалось равным
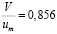 . (1.3)
. (1.3)
Затем Христен [28] получил эпюру скоростей в виде параболы восьмой степени, ветви которой, выходя из противоположных точек на стенке, встречались на оси под некоторым углом, что являлось недостатком формулы.
Было установлено также, что сужение потока приводит к выравниванию распределения скоростей. Так, при истечении из конической насадки Фримен [28] определил, что
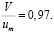 (1.4)
(1.4)
Вероятно, что Б. Сен-Венан был первым, кто заметил, что движение воды в широких трубах и руслах невозможно объяснить, если не предположить, что «вода образует в них вихри и именно тем более сильные, чем больше поперечное сечение потока» [28].
Далее, Т. Карман [28] для гладких стенок определил, что соотношение в трубах средней и максимальной скоростей составляет
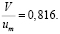 (1.5)
(1.5)
Это утверждение оказалось ошибочным.
Проблемой гидравлических сопротивлений трубопроводов исследователи занимались более 250 лет. В [41], например, упоминаются опыты Купле, выполненные еще в 1732 г.
Х. Дарси предложил в 1858 г. формулу для «избытка» скорости
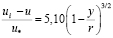 .
.
Х. Базен [36], в своих опытах установил, фактически, независимость закона распределения скоростей по сечению трубы от причин, обусловливающих касательное напряжение, выразив этот постулат формулой
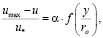 (1.6)
(1.6)
где umax – скорость на оси трубы; u – скорость в текущей точке; r0 – радиус трубы; y – расстояние от стенки; u* – динамическая скорость; α – постоянный коэффициент.
По-видимому, этот вывод Х. Базена послужил толчком к получению «универсальных» формул для распределения осреднённых скоростей.
2. Начальная стадия разработки основ для расчёта распределения осреднённых скоростей в простейших канонических течениях жидкости
Надежда на возможность разрешения этой проблемы появилась после получения в 1895 г. О. Рейнольдсом осредненных уравнений турбулентного движения, хотя к тому времени уже имелись соответствующие эмпирические формулы для расчета распределения осредненных скоростей, – парабола М. Базена, парабола Х. Дарси (они дают серьёзные расхождения в области, прилегающей к твердым границам). Но еще ранее Ж. Буссинеск (1877 г.) предложил выразить касательные турбулентные напряжения 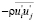 через коэффициент турбулентной вязкости nТ в виде соотношения, постулированного
через коэффициент турбулентной вязкости nТ в виде соотношения, постулированного
И. Ньютоном для ламинарных течений, то есть в виде (1.7):
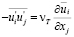 , (2.1)
, (2.1)
где – ui и uj пульсационные компоненты скорости; ui – компоненты осредненных скоростей; xi – координатное направление.
Сам Ж. Буссинеск понимал, что nТ не является физическим свойством жидкости, а представляет собой некий коэффициент незнания, функцию координат, отображающую особенности турбулентного течения жидкости в данной области (при неустановившемся течении она зависит и от времени). Значение nТ определяется исключительно экспериментальным путем с помощью выражения (2.1), для чего необходимо уметь измерять вторые одноточечные моменты 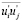 и
и 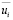 .
.
Практически все авторы исходят из признания для продольно однородных потоков модели, предложенной Ж. Буссинеском [39], связывающей турбулентные напряжения Рейнольдса с градиентом осредненных скоростей подобно закону Ньютона для ламинарных течений, путем введения виртуальной турбулентной вязкости.
Попытки распространить предложение Ж. Буссинеска на более сложные виды течения приводили последовательно к повышению требований к nТ, которое в разных случаях должно быть либо скалярной, либо векторной функцией, либо тензором четвертого ранга [21]. Этих случаев в дальнейшем не касаемся. Отметим, что при установившемся продольно – однородном турбулентном течении nТ представляет собой функцию лишь одной (поперечной) координаты, однозначно связанной c 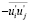 :
:
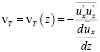 , (2.2)
, (2.2)
где x – продольная, а z – поперечная координаты.
Предложение Ж. Буссинеска представляется наиболее удачным (по крайней мере, для последнего случая) по сравнению с другими возможными тем, что позволяет объединить ламинарные τл и турбулентные τТ касательные напряжения одним выражением:
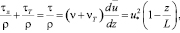 (2.3)
(2.3)
где u* – динамическая скорость; L – либо ro (радиус трубы), либо H (глубина плоского потока), либо δ – толщина пограничного слоя.
Из уравнения (2.3) получается простое дифференциальное уравнение первого порядка для определения осредненной скорости:
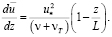 (2.4)
(2.4)
Решение уравнения (2.4) записывается в интегральной форме:
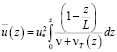 . (2.5)
. (2.5)
Для реализации зависимости (2.5) требуется знать nТ = nТ(z).
Имеются многочисленные попытки решения указанной задачи на базе уравнений Рейнольдса, которые, к сожалению, оказываются незамкнутыми. Сами же попытки сводились к формулированию неких гипотез, созданию моделей строения турбулентного потока, использованию для замыкания исходных уравнений экспериментальных данных и сопоставлению получаемых решений с опытом. Некоторые модели дали мощный импульс развитию собственно теории турбулентности (Л. Прандтль, Дж. Тейлор, А.Н. Колмогоров и многие другие). Однако впоследствии введенные на начальном этапе некоторые понятия оказались неправомерными и в настоящее время имеют лишь историческое значение. К ним можно отнести понятие о «ламинарном пристенном подслое», «длине пути смешения» и т.п. Опыты Х. Рейхардта [55], Д. Лауфера [51], А. Фейджа [46], Р. Фогельполя [59], В.Б. Гуссака [13] и других вполне доказательно их опровергают. В статье кратко излагаются основные этапы решения проблемы распределения осреднённых скоростей в простейших канонических течениях жидкости, к которым принято относить течения в круглых трубах, плоских равномерных потоках и погранслоях на плоских пластинах при нулевом градиенте давления.
3. Развитие понятия о турбулентной вязкости
Ранее указывалось, что хотя турбулентное течение начали интенсивно исследовать после получения О. Рейнольдсом осреднённых по времени (кстати, в его работе рассматривались и другие методы осреднения) уравнений движения турбулентных потоков, но и до этого периода проводились многочисленные (большей частью неудачные) попытки проникнуть в тайну турбулентности. Более того, и до сих пор не существует законченного математического аппарата описания турбулентных течений. В этих условиях основную роль приходится отводить накоплению экспериментальных сведений о различных аспектах проявления турбулентности, а также применению методов теории подобия и размерностей к анализу простейших случаев турбулентных течений.
Были сформулированы некоторые основополагающие понятия и определения. Весьма важным оказалось представление и истолкование Х.А. Лоренцем [52] понятия о кажущихся турбулентных напряжениях 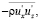 которые впоследствии были названы рейнольдсовыми. Было введено понятие о динамическом и кинематическом турбулентных коэффициентах вязкости, которые также имеют смысл, отличный от физической вязкости. С помощью этого понятия, как указывалось, турбулентные касательные напряжения (или вторые одноточечные моменты) связывались с градиентами поля скоростей (3.1).
которые впоследствии были названы рейнольдсовыми. Было введено понятие о динамическом и кинематическом турбулентных коэффициентах вязкости, которые также имеют смысл, отличный от физической вязкости. С помощью этого понятия, как указывалось, турбулентные касательные напряжения (или вторые одноточечные моменты) связывались с градиентами поля скоростей (3.1).
Согласно воззрению Ж. Буссинеска введенная им турбулентная (виртуальная) вязкость является скалярной величиной.
Практически все авторы исходят из признания для продольно однородных потоков модели, предложенной Ж. Буссинеском [39], связывающую турбулентные напряжения Рейнольдса с градиентом осредненных скоростей подобно закону Ньютона для ламинарных течений, путем введения виртуальной турбулентной вязкости.
В осесимметричных продольно-однородных потоках кинематический турбулентный коэффициент вязкости νТ представляет собой функцию одного независимого переменного – расстояния от стенки z, то есть
νТ = νТ(z) (3.1)
То же и в плоском продольно-однородном потоке.
В равной мере сказанное относится и к коэффициенту турбулентной теплопроводности.
В дальнейшем делались попытки обобщения понятия вихревой вязкости и представления её в виде скаляра
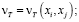 (3.2)
(3.2)
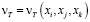 (3.3)
(3.3)
или в виде вектора 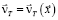 .
.
Эти возможности проанализированы, например, в [22]. Оказалось, что наиболее подходящим способом выражения вязкости в общем случае является представление её в виде тензора четвертого ранга. Ясно, что это обстоятельство делает крайне сомнительным возможность её экспериментального определения.
В [31] указывается, что провозглашение Ж. Буссинеском аналогии между хаотическим движением вихрей и случайным движением молекул в разреженных газах весьма уязвимо. Её недостатком является полная обоснованность только для продольно-однородного турбулентного течения. Попытки критики применения буссинесковой вязкости при анализе продольно-однородного турбулентного течения не могут иметь никакого обоснования, так как связь второго одноточечного момента с градиентом осредненного течения имеет тождественный характер. Единственным, но подавляющим преимуществом предложения Ж. Буссинеска является аналогия вводимых выражений соответствующим «вязким» членам в уравнениях Навье-Стокса, что способствует их объединению при последующем анализе.
На этот счет Г.И. Баренблатт высказывает безапелляционное мнение, «что для потока с поперечным сдвигом соотношение
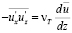
представляет собой простое преобразование и не несет в себе никакой дополнительной гипотезы» [5].
В.М. Маккавеев [19] полагал, что коэффициент турбулентной вязкости может в более сложных случаях течения жидкости проявляться как вектор. Однако в общих случаях течения жидкости, как показал О.Ф.Т. Робертс [51], νТ имеет тензорную природу. В [21] показано, как упоминалось, что данный коэффициент в этом случае должен выражаться тензором четвертого ранга.
Выражение, предложенное Ж. Буссинеском, предпочтительнее иных лишь тем, что позволяет выразить суммарно касательные напряжения наиболее простым образом:
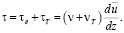 (3.4)
(3.4)
Однако, полученные, исходя из грубой модели, результаты потребуют внесения всё новых и новых экспериментальных поправок. Проиллюстрировать это обстоятельство можно на примере знаменитой формулы для распределения осредненных скоростей Л. Прандтля [53].
Во-первых, сразу же обнаружилось, что она не удовлетворяет условиям на стенке и оси потока. Потребовалось ввести надуманные понятия: «ламинарный пограничный слой» и «длина пути смешения». Этого оказалось недостаточно, и был введён еще целый ряд поправок Е. Ван Дристом [6], Р. Дейслером [43], Д. Коулзом [40], Д. Ротта [24], П. Жульеном [48] и др.
4. Развитие представлений о строении пристенного слоя
Первоначально Л. Прандтль [53] условно разделил турбулентный поток на основную часть – турбулентное ядро, и тонкий пограничный слой с ламинарным режимом течения толщиной dл =11.6 обоснованная гипотеза многократно подвергалась и экспериментальной проверке и критике и, в конечном счёте, полному отторжению.
Затем К. Тейлор, исходя из необходимости повышения точности решения задач теплообмена, ввел пограничный слой, разделенный на две зоны. Во внутреннем масштабе, за единицу длины в котором принято соотношение 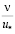 , границы этих зон определялись расстояниями от твёрдых стенок, равными 5
, границы этих зон определялись расстояниями от твёрдых стенок, равными 5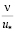 и 30
и 30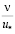 , причем в каждой зоне задавался свой закон распределения скоростей.
, причем в каждой зоне задавался свой закон распределения скоростей.
К настоящему времени упомянутые и схожие с ними гипотезы достаточно устарели. Так, например, уже опыты А. Фейджа и Х. Тауненда [46], В.Б. Гуссака [13] и др. показали, что ламинарного пограничного слоя не существует, а турбулентные пульсации скорости и давления достигают твердой стенки. Предположение о существовании прилегающего к стенке подслоя, толщина которого постоянна, и течение в котором ламинарно, было быстро отброшено [68]. Введенная Л. Прандтлем «длина пути смешения» была, фактически, также отвергнута.
А. Фейдж и Х. Тауненд [46] проводили исследование турбулентного течения при помощи ультрамикроскопа и установили, что до расстояния 0,0006 мм от стенки сохраняется турбулентное движение частиц.
Выполненные В.Б. Гуссаком наблюдения с использованием микрокиносъемки позволили ему прийти к выводу о том, что «при турбулентном движении пограничный слой в противоположность мнению Прандтля не имеет ламинарного характера». Тем не менее, мнение о том, что «несмотря на непрерывно развивающуюся технику экспериментирования, еще очень мало известно об условиях течения вблизи стенки в турбулентном потоке» [4], остается справедливым до сих пор.
Не останавливаясь далее на критике понятия « ламинарный подслой», приведём приговор, вынесенный ему в [21] ещё в 1965 году: «Раньше вместо названия вязкий подслой часто употреблялось выражение ламинарный подслой, поскольку предполагалось, что движение в пределах этого подслоя является ламинарным. В дальнейшем, однако, непосредственные ультрамикроскопические наблюдения движения частиц, взвешенных в жидкости около стенки (Фейдж и Тауненд [46]) подкреплённые затем и данными тонких термоанемометрических измерений (Лауфер [51]), показали, что хотя профиль средней скорости внутри рассматриваемого подслоя и совпадает с профилем скорости безнапорного плоскопараллельнного ламинарного течения, течение в нём всё же не является ламинарным, а сопровождается заметными турбулентными пульсациями. Поэтому в настоящее время термин «ламинарный подслой» представляется мало удачным.
5. Развитие представлений о влиянии степени шероховатости русел
Ж. Грове [47] сумел доказать, что при увеличении шероховатости стенок соотношение 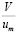 уменьшается. Целый ряд исследователей пришли затем к результату, что турбулентная вязкость на расстоянии 2/3 r0 от центра трубы остается постоянной, а затем резко падает по направлению к стенке. Р. Мизес ввел понятие «относительная шероховатость»
уменьшается. Целый ряд исследователей пришли затем к результату, что турбулентная вязкость на расстоянии 2/3 r0 от центра трубы остается постоянной, а затем резко падает по направлению к стенке. Р. Мизес ввел понятие «относительная шероховатость» 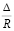 ;
; 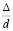 ;
; 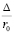 .
.
Роль шероховатости стенки была наглядно доказана известными опытами И. Никурадзе, согласно их результатам установились понятия о «гидравлически гладких» поверхностях, вполне шероховатых поверхностях. Долгое время изучались зависимость коэффициента Дарси от числа Рейнольдса и относительной шероховатости, а также влияния шероховатости на распределение осредненных скоростей. На этот счет имеются различные точки зрения.
В.Н. Гончаров полагает, что «профиль скоростей плоского турбулентного потока» одинаков «для шероховатых, гладких, полушероховатых и полугладких стенок». Формула для распределения осредненных скоростей по сечению нормальному ко дну имеет по В.Н. Гончарову вид:
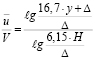 . (5.1)
. (5.1)
По этой формуле получается, что в любых зонах сопротивления распределение осредненных скоростей определяется единственным параметром, – высотой выступов шероховатости (при известном Н) Однако общеизвестно решающее влияние числа Рейнольдса в гладкостенной зоне сопротивления на значение осредненных скоростей. Цитированный вывод В.Н. Гончарова представляется сомнительным.
Под большой шероховатостью при рассмотрении течений в трубах обычно понимают такую шероховатость, при которой коэффициент Дарси принимает значение λ ≥ 0,04, что, примерно, имеет место при относительной шероховатости 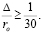
А. Фейдж и Х. Тауненд отмечают, что «на основании опытов в гладких круглых трубах известно, что распределение осредненных скоростей в радиальном направлении является параболическим вплоть до расстояния 0,8r0, считая от центра трубы» [46].
Этот закон принимается в виде
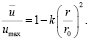 (5.2)
(5.2)
На основании работ Т. Стантона и И. Паннела в [58] приведены данные о значении k и соотношении νТ/ν .
Х. Дарси предложил в 1858 г. формулу для «избытка» скорости
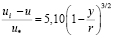 .
.
Постепенно накапливающиеся сведения в обобщенном виде позволили установить:
1. Сопоставление опытов с латунной трубкой диаметром 28 мм (И. Никурадзе) и гладкой круглой трубой к турбине диаметром 1608 мм в Бильбао привели к понятию об относительной шероховатости.
2. На расстоянии 100 d от входа в трубу с острыми кромками надежно устанавливается развитое турбулентное течение. Вход с закруглением уменьшает указанное расстояние.
3. Введенным понятием о тонком пограничном слое можно пренебречь при подсчете расхода из-за малости его влияния.
4. Режим течения в пограничном слое полагался ламинарным.
5. Л. Прандтль [28] и несколько ранее Т. Карман [28] подтвердили «закон 1/7», то есть параболическое распределение скоростей.
Перечисленные сведения были уже накоплены к 1925 г., то есть ко времени начала штурма основ теории турбулентности тремя выдающимися учеными Л. Прандтлем,
Т. Карманом и Дж. Тейлором, усилиями которых была разработана феноменологическая теория турбулентности, позволившая получить методы решения множества прикладных гидравлических (и не только) задач. Подробное описание этих работ можно найти у Г. Шлихтинга [32].
В 1935 г. Д. Тейлор выделил класс турбулентных течений, который он назвал изотропным. Для этих течений осреднённые значения функций характеристик течения не зависят от поступательного перемещения, вращения и отражения осей отсчета. Доказав возможность получения точных соотношений между осреднёнными величинами с использованием полных уравнений Навье-Стокса и неразрывности, показав их состоятельность в однородных турбулентных течениях за решеткой, он заложил основы рассмотрения турбулентности с помощью анализа динамики собственно пульсационного движения как альтернативу феноменологическим теориям, в которых рассматривается лишь влияние пульсационных движений на осредненное течение.
В дальнейшем наибольших успехов в этом направлении достигли А.Н. Колмогоров, А.М. Обухов и др.
По существующему представлению профиль осреднённой скорости в трубе продолжал делиться на две области: пристенную (или внутреннюю) и турбулентное ядро (или внешнюю). Во внутренней области только расстояние от стенки, касательное напряжение на стенке и свойства жидкости являются важными параметрами.
Из анализа размерности можно установить, что
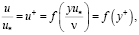 (5.3)
(5.3)
где f – безразмерное функциональное соотношение.
Уравнение (5.3) есть упоминавшийся «закон стенки». Если f независимо от числа Рейнольдса, то в рассматриваемой области существует полное подобие.
Во второй области действие стенки замедляет скорость ниже максимальной путем, который не зависит от вязкости, но зависит от расстояния от стенки, радиуса трубы и масштаба скорости в этой области. Анализ размерности приводит в этой области к соотношению
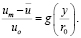 (5.4)
(5.4)
Функциональное соотношение (5.4) называют «законом дефекта скорости». Если g не зависит от числа Рейнольдса, то в этой области существует полное подобие.
Между этими двумя областями могут существовать промежуточные или пересекающиеся области, где расстояние от стенки является большой, по сравнению с внутренним масштабом 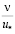 , но малой по сравнению с другим масштабом длины r0.
, но малой по сравнению с другим масштабом длины r0.
6. Основные этапы формирования подходов к получению формул для распределения осреднённых скоростей в канонических течениях
На начальном этапе формулы для распределения осреднённых скоростей в канонических течениях получались в результате обработки экспериментальных данных. Некоторые из них будут приведены далее. Затем по мере развития и уточнения представлений о закономерностях турбулентных течений жидкости менялись и совершенствовались подходы к решению рассматриваемой проблемы. Первоначально анализировались случаи течения жидкости при гладких стенках, то есть без учёта наличия на них каких бы то не было шероховатостей. Затем естественным образом наступил черёд уделить внимание и этому феномену. Наибольшие успехи были получены для зоны квадратичного сопротивления при полном игнорировании влияния вязкости жидкости. Гораздо «меньше исследованы закономерности распределения скоростей в трубопроводах, работающих в переходной области между гладким и вполне шероховатым трением, то есть в большинстве практически важных случаев, и для описания профиля скоростей в этой области не было предложено каких-либо зависимостей. В связи с этим важнейшая задача, стоящая перед исследователями, заключается в построении такой модели турбулентного потока, которая позволила бы получить зависимости для расчета и моделирования турбулентных течений в технических трубопроводах» [1]. На это были потрачены серьезные усилия многих и многих исследователей в попытке «доработать» удачную начальную модель строения турбулентного потока в трубе, приводящую к известному логарифмическому закону распределения осредненных скоростей по ее сечению (который затем был распространен до оси трубы). Этот результат, как и результаты Т. Кармана [50] и Дж. Тейлора были несовершенными, они не удовлетворяли граничным условиям на гладкой стенке и оси потока и были совершенно непригодны для расчета распределения скоростей, пожалуй, в наиболее важной его части, – в непосредственной близости от стенки. Эти начальные модели пришлось исправлять путем введения соответствующих гипотетических предположений. К их числу относятся:
– введение понятия о ламинарном пограничном слое;
– о существовании вязкого подслоя;
– об изменчивости константы Кармана по сечению потока;
– о введении двух-, трех- и многослойных пограничных слоев;
– о введении разных зависимостей для «длины пути смешения»;
– введение демпфирующих поправок и т.п.
Исходя из законов подобия для внутренней области пограничного слоя была получена универсальная формула для распределения осреднённых скоростей, известная как «закон стенки». Во внешней области имеет место самосохраняющаяся форма профиля скорости, известная как «закон дефекта скорости».
В [30] показано, что можно определить функции f(z+) и g(z+) при соблюдении их непрерывности вместе с первыми производными. В итоге получается хорошо известный результат, – обе функции являются логарифмами и сводятся к виду
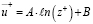 ,
,
где A и B – константы, величина которых определяется экспериментально.
Очевидно, что формула эта не может удовлетворить условиям ни на стенке, ни на оси потока, ни на границе внешней части пограничного слоя.
Обычным приемом устранения указанного недостатка на гладкой стенке является принятие вблизи нее на расстоянии z+ ≤ 5 линейного распределения осреднённых скоростей 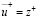 . Отметим, что в [31] этот результат назван строгим.
. Отметим, что в [31] этот результат назван строгим.
Как правило, указанные попытки преследовали цель – наилучшим образом удовлетворить имеющимся наиболее обоснованным экспериментальны данным, как правило, полученным для гладких или шероховатых труб. Все они непригодны для использования при доквадратичной зоне сопротивления. Для последнего случая наиболее известным является предложение А.Д. Альтшуля [4], получившего формулу, справедливую (по его утверждению) для распределения скоростей во всех зонах сопротивления. Но, как оказалось, и она не удовлетворяет граничным условиям.
7. Возможные подходы к решению задачи о распределении осреднённых скоростей в простейших канонических течениях жидкости
Осредненная скорость при продольно-однородном течении жидкости связана с кинематическим коэффициентом турбулентной вязкости простым соотношением (2.4).
Если бы νТ = νТ(z), входящее в (2.4) было заранее известно, то определение осредненной скорости сводилось бы к решению уравнения (2.4), что само по себе не представляет никаких трудностей (по крайней мере, для получения численных результатов).
Перед исследователями, столкнувшимся с незнанием закономерности νТ = νТ(z), встала дилемма – либо ждать, когда будет накоплено достаточное количество экспериментальных данных, обобщение которых позволило бы аппроксимировать зависимость νТ = νТ (z) во всем диапазоне изменения 0 ≤ z ≤ L, – либо попытаться интуитивно уловить основные особенности этой закономерности, выразить ее аналитически, после чего путь к получению зависимости 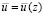 будет открыт; νТ = νТ (z) из формулы (5.4) не может привести к ошибочному решению задачи об отыскании
будет открыт; νТ = νТ (z) из формулы (5.4) не может привести к ошибочному решению задачи об отыскании 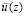 , так как оба выражения, то есть формула (2.4) для определения
, так как оба выражения, то есть формула (2.4) для определения 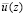 и формула (2.2) для экспериментального определения ν(z) представляют собой тождественные выражения.
и формула (2.2) для экспериментального определения ν(z) представляют собой тождественные выражения.
Оказалось, что экспериментальное определение v(z) представляет собой задачу исключительной сложности. Она, несмотря на интенсивное развитие измерительной техники, не решена до сих пор. В частности, пока еще нет надежных данных об изменении второго одноточечного момента 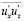 в пристенной зоне на расстояниях, меньших 3
в пристенной зоне на расстояниях, меньших 3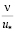 .
.
Поскольку при отсутствии соответствующей измерительной техники невозможно получить νТ(z) с помощью выражения (2.2), первоначально исследователям пришлось для получения формулы распределения осредненных скоростей идти первым из возможных двух путей.
Путь первый заключается в том, что с помощью неких правдоподобных рассуждений νТ(z) задается в том или ином виде.
Например, Л.Д. Ландау [16], применив анализ размерностей, пришел к заключению, что должно быть
νТ(z) = 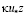 , (7.1)
, (7.1)
где k – константа, z – расстояние от стенки.
Л. Прандтль и Т. Тейлор ввели
νТ(z) = 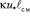 , (7.2)
, (7.2)
где 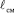 – длина пути смешения.
– длина пути смешения.
В этом случае получаются логарифмические эпюры распределения скоростей. Если задать νТ(z) иначе, получатся другие формулы.
Полученные при задании эпюры νТ(z) зависимости сравниваются с экспериментальными эпюрами осредненных скоростей. Обнаруженное расхождение неминуемо приходится «списывать» на несовершенство принятой формулы для νТ(z) и искать выход во введении тех или иных поправок. Число таких поправок весьма велико, и оно все еще продолжает приумножаться. Наиболее известны поправки Д. Коулза [40], Е.Р. Ван Дриста [6], Д. Ротта [24], П. Жульена [48] и многих других ученых. В результате постоянную Кармана предлагают считать изменяющейся в диапазоне от 0,3 до 0,6 и более. Есть предложения считать её не константой, а функцией z; множество выражений предложено для задания 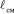 (z) и т.п.
(z) и т.п.
К числу достижений феноменологических теорий следует отнести, в первую очередь, разработку моделей строения турбулентного потока.
К числу тех, кто отказался от понятия «ламинарный подслой» относится Х. Рейхардт [55], предположивший, что пульсации скорости проникают до твердой стенки. Он ввел при y+ < 6 добавочное к ламинарному турбулентное напряжение τТ зависимостью:
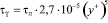 , (7.3)
, (7.3)
при y+ = 6 значение τТ оказывается равным τТ = 0,193 τл.
Таким образом, по Х. Рейхардту, касательные турбулентные напряжения убывают в направлении стенки пропорционально y5, что не подтверждается современными измерениями, согласно которым убывание происходит пропорционально y3. Таким образом, есть основание анализируемые понятия в настоящее время считать имеющими историческое значение.
Ту же задачу можно решить, следуя вторым путем.
Путь второй. Ясно, что если бы удалось найти зависимость, описывающую распределение nТ во всём диапазоне изменения z (от нуля до Н), то в этом случае задача была бы решена аналитическим или численным простым интегрированием выражения в правой части исходного уравнения. Для достижения этой цели необходимо было создать высокоточные методы измерений скоростей и автоматизации обработки полученных данных. Примерно до расстояния в 5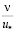 надежно измеряется и второй статистический момент. Следовательно, почти для всей толщи потока имеется основание для построения модели распределения νТ(z) и решения задачи об эпюре осредненной скорости. Что для этой цели необходимо принять во внимание?
надежно измеряется и второй статистический момент. Следовательно, почти для всей толщи потока имеется основание для построения модели распределения νТ(z) и решения задачи об эпюре осредненной скорости. Что для этой цели необходимо принять во внимание?
Во-первых, О. Рейнольдс [56] указал, что энергия турбулентности в уравнении баланса энергии турбулентности поддерживается за счет отбора её от осредненного течения, за что ответственны члены вида 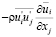 , причем при
, причем при 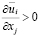 он объявил
он объявил 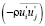 положительно определённой функцией координат. Такое предложение сочеталось с представлением о турбулентности как о каскадном процессе дробления крупных вихрей на более мелкие, еще более мелкие и т.д., до мельчайших, в которых механическая энергия диссипирует. Из такого представления однозначно следует, что если записать выражение
положительно определённой функцией координат. Такое предложение сочеталось с представлением о турбулентности как о каскадном процессе дробления крупных вихрей на более мелкие, еще более мелкие и т.д., до мельчайших, в которых механическая энергия диссипирует. Из такого представления однозначно следует, что если записать выражение 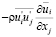 в виде
в виде
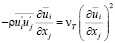 , (7.4)
, (7.4)
то коэффициент турбулентной вязкости nТ(z) > 0. Другими словами, это означает существенную положительность nТ(z) и необратимость процесса передачи механической энергии от осредненного к турбулентному движению.
Большинство исследователей до сих пор жестко придерживается этого мнения. Выполненный в [7, 8] квадрантный анализ значений второго одноточечного момента в четырех квадрантах показал, что значения 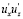 имеют перемежающийся характер, то есть во всей толще потока наблюдается проявление указанных моментов как положительных, так и отрицательных. Однако в турбулентном ядре преобладающим является фиксация
имеют перемежающийся характер, то есть во всей толще потока наблюдается проявление указанных моментов как положительных, так и отрицательных. Однако в турбулентном ядре преобладающим является фиксация 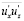 < 0. Затем по мере приближения к пристенному слою влияния моментов
< 0. Затем по мере приближения к пристенному слою влияния моментов 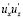 > 0 увеличивается, а
> 0 увеличивается, а 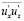 , оставаясь отрицательной величиной, уменьшается по абсолютной величине. Этот факт заставил А.С. Монина [21] заявить, что, так как имеющиеся данные измерений
, оставаясь отрицательной величиной, уменьшается по абсолютной величине. Этот факт заставил А.С. Монина [21] заявить, что, так как имеющиеся данные измерений 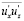 , вплоть до расстояний от стенки порядка 5
, вплоть до расстояний от стенки порядка 5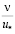 , показывают, что они неизменно отрицательны, то интуитивно можно предположить, что это положение будет справедливым до гладкой стенки, то есть, что они отрицательны всюду.
, показывают, что они неизменно отрицательны, то интуитивно можно предположить, что это положение будет справедливым до гладкой стенки, то есть, что они отрицательны всюду.
Тем не менее, данные [29] свидетельствуют о том, что на расстоянии ≈ 2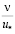 от стенки моменты
от стенки моменты 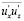 становятся нулевыми. Это дает основание предположить, что в диапазоне расстояний от стенки 0 < δz < 2
становятся нулевыми. Это дает основание предположить, что в диапазоне расстояний от стенки 0 < δz < 2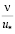 момент
момент 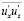 может стать положительным, что означает, что в этой области коэффициент турбулентной вязкости νТ(δz) становится отрицательным.
может стать положительным, что означает, что в этой области коэффициент турбулентной вязкости νТ(δz) становится отрицательным.
8. Генерировании идей о распределении кинематического коэффициента турбулентной вязкости в канонических потоках
Наиболее простым результатом явилось получение Л.Д. Ландау [16] с помощью анализа размерностей выражения для nТ в виде:
nТ = k u* y, (8.1)
где y – расстояние до стенки.
Этот результат легко приводит к получению логарифмического закона распределения скоростей. Многие авторы пытались далее с помощью многочисленных экспериментальных исследований о распределении осредненных скоростей использовать полученные данные для определения νT из формулы
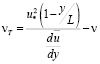 . (8.2)
. (8.2)
Этот путь не мог привести к получению надежных данных из-за невозможности достаточно точного измерения скоростей на малых расстояниях от стенки и, в особенности, необходимости определения их градиентов, что сопряжено с колоссальными погрешностями. Этому приему сопутствовало формулирование гипотетических предложений о виде зависимости nТ = nТ(y/L). Каждой из подобных гипотез соответствовала своя закономерность.
В качестве примера приведем несколько результатов.
Не будем останавливаться на классической «длине пути смешения l», которую Л. Прандтль ввел вместо «расстояния до стенки y» по Л.Д. Ландау, и которую, в свою очередь, многие исследователи превратили в функцию 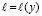 . Многие из них придерживались мнения (по Л. Прандтлю), что на малом расстоянии dl от стенки режим движения является ламинарным.
. Многие из них придерживались мнения (по Л. Прандтлю), что на малом расстоянии dl от стенки режим движения является ламинарным.
Д. Ротта [24] предположил, что
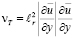 , (8.3)
, (8.3)
где 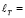
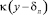 ;
; 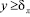 ; dл – толщина ламинарного слоя.
; dл – толщина ламинарного слоя.
Тогда формула для осредненной скорости принимает вид:
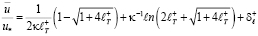 , (8.4)
, (8.4)
где 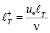 ;
; 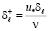 .
.
Х. Рейхардт [55] принял, что
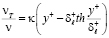 . (8.5)
. (8.5)
Окончательная формула для распределения 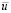 получена им в виде:
получена им в виде:
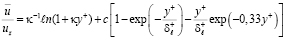 , (8.6)
, (8.6)
где c – численная константа.
Р.Г. Дайслер [44] принял, что
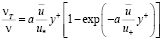 , (8.7)
, (8.7)
где а – численная константа.
Распределение осредненных скоростей по Р.Г. Дайслеру находится численным интегрированием формулы (2.4) при учете (8.7).
Ван Дрист выражению для пути смешения lT Л. Прандтля предложил придать видоизмененную форму
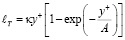 , (8.8)
, (8.8)
что эквивалентно принятию νT в виде
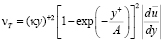 . (8.9)
. (8.9)
Формула для расчета распределения осредненных скоростей тогда имеет вид
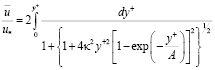 . (8.10)
. (8.10)
Д.Ж. Коулс [40] предложил ввести в формулу для распределения скоростей чисто эмпирическую поправочную функцию, подобно тому, как это сделал С.Б. Милликен при анализе течения в следе. Поэтому Д.Ж. Коулс назвал введенную функцию законом следа. С такой поправкой логарифмический закон распределения скоростей имеет вид:
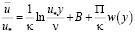 , (8.11)
, (8.11)
где П = 0,55, В = 5,1 и k = 0,4 для пограничного слоя при нулевом градиенте давления.
И.О. Хинце [30] представил функцию w(y) в виде:
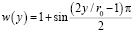 . (8.12)
. (8.12)
Б. Худимото предложил задавать касательное турбулентное напряжение τT в виде
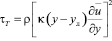 , (8.13)
, (8.13)
где yл – толщина вязкого подслоя. При y = yл эпюра скорости имеет разрыв во второй производной с обеспечением плавного перехода от линейного закона к логарифмическому.
М.Д. Миллионщиков [20] предложил существование раздельного влияния на длину пути смешения и, следовательно, на коэффициент νT расстояния от стенки и выступов шероховатости, причем подслой толщиной y1 может быть утоплен между выступами шероховатости
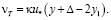 (8.14)
(8.14)
Для пограничных течений Ф.Х. Клаузер для внешней области предложил для νT зависимости:
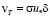 (Клаузер – 1),
(Клаузер – 1),
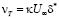 (Клаузер – 2),
(Клаузер – 2),
где σ – эмпирическая константа; d – толщина пограничного слоя; U∞ – скорость невозмущенного потока; δ* – толщина вытеснения пограничного слоя. Для длины пути смешения Л. Прандтля принималось l = λδ, где l = 0,09.
В модели Себеси – Смита [23] константа k = 0,0168. Кроме того, на влияние малых чисел Рейнольдса была введена поправка в виде эмпирической зависимости:
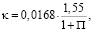
где
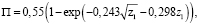
где 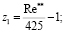
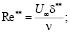 δ** – толщина потери импульса.
δ** – толщина потери импульса.
Перечень подобных подходов можно было бы продолжить. Они продолжаются и по сей день (см., например [48]).
9. Развитие методов решения задачи о распределении осреднённых скоростей в плоских равномерных потоках
9.1. Развитие методов решения задачи о распределении осреднённых скоростей в плоских равномерных потоках
Ученик Х. Дарси Х. Базен получил формулу, именуемую «параболой Базена»:
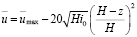 . (9.1)
. (9.1)
Однако в придонной зоне эти формулы не приводят к удовлетворительным результатам.
К наличию параболического закона распределения скоростей в турбулентном потоке склонялись также А.А. Таунсенд [27], Ж. Конт-Белло [15] и др.
А.А. Таунсенд [27] отмечает, что «по-видимому, не имеется физических оснований верить в справедливость предположения о существовании виртуальной вязкости, постоянной внутри турбулентной жидкости, однако это предположение приводит к очень точным описаниям распределения осредненной скорости в автомодельных потоках и, несомненно, является весьма полезной гипотезой, которой и следует пользоваться».
9.2. Развитие методов решения задачи о распределении осреднённых скоростей в круглых трубах
Постепенно укоренилось мнение о таком строении продольно-однородного турбулентного потока:
– у стенки существует вязкий подслой с линейным распределением осреднённых скоростей, толщина которого варьируется около значения 5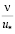 ;
;
– затем следует буферный слой с законом распределения скоростей, называемым «законом стенки», толщиной 5 < y+ ≤ 30;
– в следующем слое закон распределения становится логарифмическим. н простирается до значений
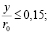
– затем следует турбулентное ядро, в котором принято называть распределение скоростей законом «дефекта скорости» или «дефицита скорости»:
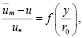
где за 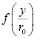 также принимается логарифмический закон.
также принимается логарифмический закон.
По мере возрастания требований к точности закономерностей, которым подчиняются распределения осреднённых скоростей для производства теплотехнических расчетов, анализа взвесенесущей способности турбулентных потоков, а также с получением новых экспериментальных данных с помощью новейшей измерительной техники, рядом ученых были внесены поправки к основной (логарифмической) формуле при соответствующих научных обоснованиях. В основном они касались вида формулы для прандтлевой длины пути смешения.
В дальнейшем гипотеза об универсальности закона распределения осреднённых скоростей стала подвергаться все большей критике. Появились высказывания в пользу того факта, что нельзя представить себе условную границу между зонами, в которых влияние на движение стенка и вязкость оказывают, а в которой такое влияние отсутствует полностью. Появилось представление о взаимоперекрывающихся зонах, понятие о неполном подобии, о влиянии числа Рейнольдса в некоторых специфических районах эпюры скоростей.
Первым, кто исследовал эту проблему, был Г.И. Баренблатт [5]. Результаты его разработок [34, 35] были восприняты неоднозначно и названы Б. Кипра [60] «в высшей степени сомнительными».
Тем не менее, Г.И. Баренблатт [34, 35] при развитии теории неполной автомодельности предполагает наличие в окрестности пристеночной области слоя с постоянным турбулентным напряжением сдвига, что объясняется его малостью у стенки. При этом игнорируется тот факт, что стремление 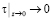 , очевидно, не означает, что и
, очевидно, не означает, что и
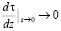 .
.
Многими авторами отмечается, что степенная формула для распределения осреднённых скоростей в трубах ничуть не хуже логарифмической формулы, но обе они непригодны как вблизи стенок, так и в приосевой зоне.
Формулы степенного типа
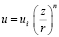 (9.2)
(9.2)
дают на стенке при z = 0 значение
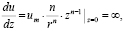 (9.3)
(9.3)
то есть эти формулы вблизи твердой поверхности не имеют физического смысла. Следовательно, для анализа течений вблизи твердых стенок они непригодны, их можно применять лишь при 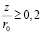 [4].
[4].
9.3. Развитие методов решения задачи о распределении осреднённых скоростей в пограничных слоях
Исследования распределения осреднённых скоростей в пограничном слое на плоской пластине при нулевом градиенте давления
Течение в пограничном слое на плоской пластине даже при нулевом градиенте давления не является продольно-однородным, так как его толщина δ непрерывно увеличивается в направлении течения (в направлении x) и, кроме того, возникает малая компонента скорости 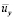 . Толщина пограничного слоя δ не может быть определена точно, ввиду её асимптотического поведения. Принято считать, что пограничный слой простирается от стенки до точки, где скорость отличается от скорости внешнего потока на некоторую долю последней (обычно её принимают равной 1 %).
. Толщина пограничного слоя δ не может быть определена точно, ввиду её асимптотического поведения. Принято считать, что пограничный слой простирается от стенки до точки, где скорость отличается от скорости внешнего потока на некоторую долю последней (обычно её принимают равной 1 %).
По Тейлору в области погранслоя на пластине толщиной δ, где выполняется «закон стенок», можно выделить при нулевом градиенте давления зоны:
– ламинарный подслой 0 < y+ ≤ 4;
– переходная зона 4 ≤ y+ ≤ 30 ÷70;
– турбулентная логарифмическая зона
y+ ≥ 30 ÷70, 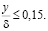
Кроме того, для внутренней области погранслоя константа Кармана может быть принята равной k = 0,41, а для внешней k = 0,267.
В настоящее время широкое распространение получила двухслойная схема строения пограничного слоя Прандтля – Клаузера [17], то есть признание за внутреннюю зону, содержащую вязкий подслой и логарифмический слой, и внешнюю зону, называемую областью «следа». Л.Г. Лойцянский [17] полагает, что большую роль во внешней области турбулентного пограничного слоя играют «внешние эффекты памяти», рассмотренные Бультьесом [17].
В [13] приведена краткая сводка формул для распределения осреднённых скоростей в погранслое при нулевом градиенте давления с указанием на невозможность описать этот закон единой формулой.
В случае шероховатых пластин с равнозернистой шероховатостью важную роль (как для труб – относительная шероховатость Δ/r0) играет её аналог, отношение высоты выступа шероховатости к толщине пограничного слоя Δ/δ. Между этими понятиями, однако, имеется существенное различие: в то время как для трубы Δ/r0 = соnst, отношение Δ/δ по мере увеличения x уменьшается из-за постепенного увеличения толщины пограничного слоя. Может случиться [32], что пластина недалеко от переднего носика может вести себя как вполне шероховатая, на некотором удалении от него, как в переходной области, а на большом расстоянии от носика (если пластина достаточно длинная), – как гладкая. Это резко различает турбулентные течения в трубе от обтекания пластины. Границы же между этими зонами, как и для труб, определяются значениями
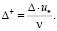
Более того, оказалось, что и для шероховатой пластины её сопротивление можно определить путем пересчета, аналогичного пересчету для гладкой пластины. Он был выполнен Л. Прандтлем и Г. Шлихтингом с использованием опытных данных И. Никурадзе для труб с песочной шероховатостью и логарифмического закона распределения скоростей [32].
Ф. Хама [49] предложил формулу для описания распределения осреднённых скоростей в области
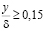 .
.
Она имеет вид
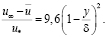 (9.4)
(9.4)
10. Современные представления о возможности существования отрицательного значения кинематического коэффициента турбулентной вязкости
В настоящее время, пожалуй, наиболее распространенным мнением о возможности появления зон течения в турбулентном потоке, в которых существует отрицательная турбулентная вязкость, является полное их отрицание. Это означает, что в случае продольно однородного течения (в частности, в круглой трубе) не может существовать зон, в которых градиент скорости превышал бы его значение у стенки, то есть при увеличении у градиент осредненной скорости должен монотонно убывать. Ясно, что это связано со знаком осредненных вторых моментов 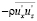 , которые принято считать всегда отрицательными. Этому есть ряд объяснений, не выдерживающих, на наш взгляд, строгой критики.
, которые принято считать всегда отрицательными. Этому есть ряд объяснений, не выдерживающих, на наш взгляд, строгой критики.
Подобного мнения придерживается, например, академик М.А. Великанов: «Как показывают и эксперимент, и теория, произведение 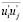 всегда отрицательно», что эквивалентно утверждению, что вихревая вязкость νТ всегда положительна.
всегда отрицательно», что эквивалентно утверждению, что вихревая вязкость νТ всегда положительна.
Г. Шлихтинг более осторожно отмечает, что « в целом положительные пульсации 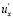 «обычно» связаны с отрицательными пульсациями
«обычно» связаны с отрицательными пульсациями 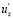 , а отрицательные
, а отрицательные 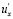 – с положительными
– с положительными 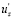 , и поэтому следует ожидать, что осредненное значение
, и поэтому следует ожидать, что осредненное значение 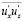 не равно нулю и притом имеет отрицательный знак» [32].
не равно нулю и притом имеет отрицательный знак» [32].
У Д.В. Штеренлихта находим: «Произведение 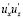 (и других разноименных пульсационных составляющих скорости) – всегда отрицательные величины» [143].
(и других разноименных пульсационных составляющих скорости) – всегда отрицательные величины» [143].
А. Рейнольдс замечает, что «гипотеза коэффициента турбулентной вязкости означает, что величина νТ конечна и положительна» .
Некоторые исследователи полагают, что появление при проведении расчетов отрицательной турбулентной вязкости является неким курьезом, либо игрой вычислительных погрешностей и т.д.
Отметим, что проблема отрицательной турбулентной вязкости обсуждается крайне скупо и, как представляется авторам, неохотно. Пожалуй, одной из противоположностей таким работам является статья Х.А. Лоренца [52].
Разъясняя отличие молекулярной вязкости ν от введенной Ж. Бусинеском турбулентной вязкости νТ Ф. Форхгеймер утверждал, что при турбулентном движении «осредненное течение может превращаться не только в тепло, но и в вихри; пожалуй, и, наоборот, благодаря уменьшению вихрей может появиться ускорение осредненного движения; однако относительно этого опытных данных нет» [28].
В недавно вышедшем учебнике А.Д. Гиргидов полагает, что «слагаемое 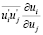 представляет собой изменение плотности энергии осредненного движения вследствие превращения этой энергии в энергию пульсационного движения (или, наоборот, превращение турбулентной энергии в энергию осредненного движения)» [11].
представляет собой изменение плотности энергии осредненного движения вследствие превращения этой энергии в энергию пульсационного движения (или, наоборот, превращение турбулентной энергии в энергию осредненного движения)» [11].
Проблема, однако, не столь очевидна, а для ее будирования имеются многочисленные, давнишние и недавние экспериментальные факты.
В [14] со всей определенностью утверждается, что объяснение направления передачи энергии может быть дано при условии отказа от традиционных представлений о всегда положительной турбулентной вязкости и введения «отрицательной» турбулентной вязкости. Понятие отрицательной турбулентной вязкости отражает как бы отрицательную генерацию турбулентной энергии турбулентности по отношению к осреднённому движению.
Тем не менее, нет оснований считать, что эта проблема замалчивается искусственно. Во-первых, имеется, например, в [25] указание, что знак величины 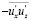 не противоречит уравнениям Рейнольдса. Во-вторых, в высокоточных опытах Т. Стантона [58], Лауфера [51] и многих других неоднократно наблюдалось превышение градиентом скорости вблизи стенки величины
не противоречит уравнениям Рейнольдса. Во-вторых, в высокоточных опытах Т. Стантона [58], Лауфера [51] и многих других неоднократно наблюдалось превышение градиентом скорости вблизи стенки величины
В [26] автор полагает, что распространённая точка зрения на передачу турбулентной энергии нуждается в уточнении.
В.М. Лятхер прямо указывает, что при малых y+ << 1 «турбулентные напряжения положительны, скорость генерации турбулентности отрицательна – энергия переходит от пульсационного движения к осредненному. Этот результат не противоречит прямым измерениям у стенки» [18].
Г. Бетчелор, рассматривая результаты экспериментальных исследований Таунсендом строения плоского следа за цилиндром [37], обнаружил наличие зон с отрицательными турбулентной вязкостью и турбулентной теплопроводностью. Подобного рода явления (проявление отрицательных турбулентных вязкости и теплопроводности) получили специальное наименование – контрградиентных переносов импульса и температуры.
Обзор и анализ этих явлений был произведен С. Эшкинази и Ф.Ф. Эйреном [45], которые трактовали их как «реверс энергии», передачу кинетической энергии мелкомасштабными вихрями крупномасштабным, то есть от пульсационного осредненному движению.
С. Бегье [38] наблюдал отрицательное порождение энергии в слоях смешения при нулевом градиенте давления.
Вероятно, можно согласиться также с мнением, что лишь небольшая часть кинетической пульсационной энергии может быть возвращена осредненному движению.
Таким образом, из приведенного обзора, который можно было бы существенно расширить, следует, что контрградиентные течения не относятся к «из ряда вон выходящему» явлению, а имеют достаточно широкое распространение.
Таким образом, выявленные феномены у гладкой стенки являются следствием частичного возвращения энергии турбулентности осредненному течению. Они проявляются в виде некоторого увеличения осредненных скоростей в окрестности гладкой стенки.
Таким образом, еще раз установлено, что в вязком подслое имеет место контрградиентное течение жидкости, даже в общепринятом случае.
Более того, если принять, по Т. Карману, (что также имеет широкое распространение) распределение осредненных скоростей в буферной зоне при значениях 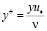 в диапазоне
в диапазоне 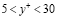 по формуле
по формуле
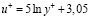 , (10.1)
, (10.1)
то в этом случае зона с отрицательной турбулентной вязкостью захватит часть и этой зоны.
Действительно, из зависимости (10.1) имеем
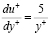 или
или 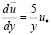 . (10.2)
. (10.2)
Подставляя этот результат в уравнение (2.4), получим
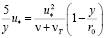 .
.
Отсюда
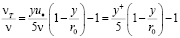 .(10.3)
.(10.3)
На границе зон y+ = 5, получаем уже известный результат νт < 0. Однако легко понять, что при еще некотором приращении Δy+ > 0 турбулентная вязкость будет продолжать оставаться отрицательной.
11. Новая модель канонических турбулентных течений жидкости
Приведенные экспериментальные данные в совокупности с формой эпюры отрицательных значений νТ(δz) вблизи от гладкой стенки дают основание построить правдоподобную модель изменения νТ(z) во всем диапазоне изменения 0 ≤ z ≤ Н. Были введены пять зон, из которых две относятся к так называемому «турбулентному ядру», то есть основной части турбулентного потока. Пристенный слой делится на три зоны.
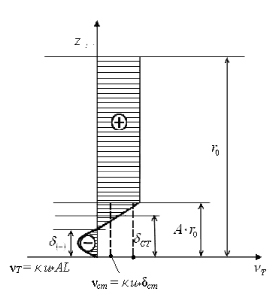
Рис. 1. Схема модели распределения коэффициента турбулентной вязкости по сечению продольно-однородного турбулентного потока при гладких стенках
Внешняя зона турбулентного ядра толщиной А·L, где L – либо радиус трубы ro, либо глубина плоского потока Н.
В этой зоне νТ > 0 и близко к своему максимальному значению. Приближённо можно для этой зоны принять νТ ≈ const = (νТ)А, то есть равенство ее значению νТ в точке А (на границе между первой и второй зонами) νТ = k u*AL.
Ко второй зоне турбулентного ядра (внутренней), где коэффициент турбулентной вязкости убывает от значения (νТ)А до значения на границе с пристенным слоем νст, по закону, который примем линейным (он широко известен):
νТ = k u* z , (11.1)
где z – расстояние от гладкой стенки. Оно меняется в пределах δст ≤ z ≤ A·L, где A < 1, а k – константа Кармана.
Пристенный слой толщиной δст, как указывалось, делится на три зоны. В зоне, примыкающей к турбулентному ядру при δст ≥ z ≥ δв, турбулентная вязкость продолжает убывать более интенсивно. В средней зоне пристенного слоя имеет место некоторое замедление убывания νТ. При этом δв ≥ z ≥ δ(–).
Наконец, непосредственно примыкающий к гладкой стенке слой очень малой толщины δ(–) (порядка 1,5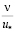 ), в котором турбулентная вязкость отрицательна, то есть νТ < 0. В этом слое возврат энергии осредненному движению превышает её отбор турбулентностью. Наличие такого графика позволяет аппроксимировать распределение νТ по всей толщине турбулентного потока и, следовательно, не прибегая к данным измерения осредненных скоростей (они нужны лишь для проверки полученных результатов), а путем прямого интегрирования (численного или аналитического) уравнения равномерного движения (11.2) получить зависимость u(z)
), в котором турбулентная вязкость отрицательна, то есть νТ < 0. В этом слое возврат энергии осредненному движению превышает её отбор турбулентностью. Наличие такого графика позволяет аппроксимировать распределение νТ по всей толщине турбулентного потока и, следовательно, не прибегая к данным измерения осредненных скоростей (они нужны лишь для проверки полученных результатов), а путем прямого интегрирования (численного или аналитического) уравнения равномерного движения (11.2) получить зависимость u(z)
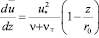 . (11.2)
. (11.2)
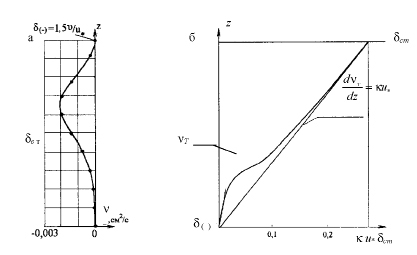
Рис. 11.2. График распределения νТ = νТ(z): а – в зоне 0 ≤ z ≤ d(–); б – в зоне d(–) ≤ z ≤ dст.
Итак, первым шагом для доведения решения задачи о распределении осредненных скоростей до логического завершения является аппроксимация распределения вихревой вязкости во всей толще продольно-однородного турбулентного потока. Опишем некоторые особенности, которые необходимо учитывать при практических расчетах:
– слой с отрицательной турбулентной вязкостью (nТ < 0), толщиной, определенной пробными расчетами в 1,5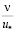 . В этом слое
. В этом слое 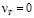 на стенке, затем уменьшается до минимального размера, а при дальнейшем росте y до значения 1,5
на стенке, затем уменьшается до минимального размера, а при дальнейшем росте y до значения 1,5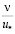 увеличивается до
увеличивается до 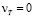 . Как указывалось, минимальное значение nТ не может превзойти –n. В дальнейших расчетах было принято
. Как указывалось, минимальное значение nТ не может превзойти –n. В дальнейших расчетах было принято 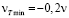 ;
;
– слой, в котором по мере роста z, нелинейно возрастает nТ, причем 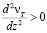 до значения
до значения 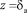 ;
;
– слой, в котором по мере роста z, нелинейно возрастает nТ, причем 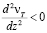 до значения
до значения 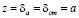 .
. 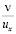 с переходом при
с переходом при 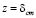 в линейную зависимость nТ = ku*z.
в линейную зависимость nТ = ku*z.
Турбулентное ядро делится на две зоны:
– первая, при 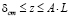 соответствует росту nТ по линейному закону, при nТ = ku*z и, следовательно, соответствует логарифмическому закону распределения осредненных скоростей;
соответствует росту nТ по линейному закону, при nТ = ku*z и, следовательно, соответствует логарифмическому закону распределения осредненных скоростей;
– вторая, при 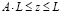 соответствует постоянному значению nТ = ku*AL, где L = r0 или Н и, следовательно, параболическому распределению осредненных скоростей.
соответствует постоянному значению nТ = ku*AL, где L = r0 или Н и, следовательно, параболическому распределению осредненных скоростей.
Соотношение толщин слоев δ(–), δb и δa принято с учетом наиболее часто повторяющихся экспериментальных данных о характерных длинах, связанных с пограничным слоем, в предположении об универсальности: d(–) : δb : δa = 1,5 : 30 : 70.
Таким образом, обозначены две основные зоны: пристенный слой и турбулентное ядро, каждая из которых подразделяется на три и две подзоны, соответственно. Условные границы между ними не признаются жесткими. Они трансформируются в зависимости от основных параметров, влияющих на течение турбулентного продольно-однородного потока, – числа Рейнольдса 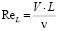 и относительной шероховатости
и относительной шероховатости 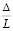 . Это означает, что введенные параметры dст; а и А являются функциями ReL и D/L в общем случае, функциями ReL при гладких стенках и только функциями D/L при шероховатых стенках.
. Это означает, что введенные параметры dст; а и А являются функциями ReL и D/L в общем случае, функциями ReL при гладких стенках и только функциями D/L при шероховатых стенках.
Поскольку выражение для параметра
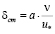
тождественным преобразованием приводится к виду
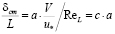 ,
,
где
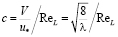 ,
,
то dст и a оказываются линейно зависимыми.
Следовательно, отысканию для идентификации эпюры распределения осредненных скоростей подлежат два параметра: a и A.
Методы их отыскания приведены в [9,10], Эта процедура сводится к решению системы двух уравнений.
12. Решение рассматриваемой задачи с использованием новой модели канонических турбулентных течений жидкости
12.1. Распределение осреднённых скоростей в пристенном слое
Далее опишем собственно реализацию предлагаемой процедуры отыскания законов распределения осредненных скоростей в направлении y, нормальном стенке.
Получение зависимости для распределения осредненных скоростей в продольно однородных потоках естественным образом базируется на формуле Буссинеска. Она позволяет при известном распределении nТ по толще потока nТ = nТ(y/L), где L = rо для трубы L = Н для плоского потока, простым интегрированием аналитически или численно получить ответ на сформулированную важную проблему.
При малых числах Red или ReH становится заметным влияние относительной толщины пристенного слоя dст/rо (это будет показано в следующем пункте). Поэтому в этом случае в уравнении (2.4) нельзя игнорировать член y/ro (или z/H). Тогда, очевидно, осредненные скорости после интегрирования (2.4) определятся выражением
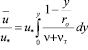 . (12.1)
. (12.1)
Имея в виду трехслойную модель пристенного слоя, толщина зон которых равна, соответственно, 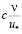 ,
, 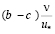 и
и 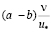 , а также, что значения nТ представлены в приведенной табличной форме, результаты послойного численного интегрирования также представлены в табличной форме.
, а также, что значения nТ представлены в приведенной табличной форме, результаты послойного численного интегрирования также представлены в табличной форме.
Значение безразмерных осредненных скоростей 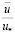 в пристенном слое δст
в пристенном слое δст
|
|
|||
|
В зоне значений
|
В зоне значений
|
В зоне значений
|
|
|
0 |
0,0000 |
a10–2(2,354–0,257 |
a10–2(19,27–2,57 |
|
1 |
a10–2(0,214–0,0002 |
a10–2(6,017–0,170 |
a10–2(19,73–2,70 |
|
2 |
a10–2(0,430–0,0009 |
a10–2(9,070–0,418 |
a10–2(20,14–2,99 |
|
3 |
a10–2(0,648–0,0021 |
a10–2(11,686–0,735 |
a10–2(20,50–3,20 |
|
4 |
a10–2(0,875–0,0038 |
a10–2(13,856–1,087 |
a10–2(20,82–3,40 |
|
5 |
a10–2(1,115–0,0061 |
a10–2(15,573–1,433 |
a10–2(21,11–3,59 |
|
6 |
a10–2(1,370–0,0092 |
a10–2(16,851–1,742 |
a10–2(21,37–3,72 |
|
7 |
a10–2(1,642–0,0129 |
a10–2(17,779–2,0004 |
a10–2(21,62–3,98 |
|
8 |
a10–2(1,898–0,0170 |
a10–2(18,422–2,235 |
a10–2(21,84–4,18 |
|
9 |
a10–2(2,134–0,0213 |
a10–2(18,886–2,415 |
a10–2(22,06–4,37 |
|
10 |
a10–2(2,354–0,0257 |
a10–2(19,269–2,571 |
a10–2(22,26–4,57 |
12.2. Распределение осреднённых скоростей во внутренней части турбулентного ядра
Так как во внутренней зоне турбулентного ядра принято распределение турбулентной вязкости по линейному закону
νт = k u* z, (12.2)
то задача о распределении осредненных скоростей по нормали к стенке в этой зоне сводится к вычислению интеграла в выражении (2.5), которое принимает вид
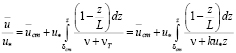 ,
,
где 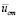 – скорость на границе пристенного слоя, L – rо (для трубы), Н (для плоского потока).
– скорость на границе пристенного слоя, L – rо (для трубы), Н (для плоского потока).
Этот интеграл после несложных преобразований сводится к табличному, использование которого приводит к следующему результату:
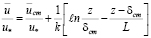 . (12.3)
. (12.3)
Из формулы (12.3) следует, что профиль осредненных скоростей одинаков во внутренней зоне турбулентного ядра как для течения в круглой трубе, так и в плоском потоке и эту зону можно именовать зоной с логарифмическим распределением скоростей.
На внешней границе внутренней зоны турбулентного ядра, то есть на расстоянии z = AL от стенки, осредненная скорость 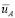 оказывается равной
оказывается равной
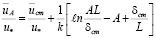 . (12.4)
. (12.4)
Эта скорость является граничным условием для отыскания распределения осредненных скоростей во внешней зоне турбулентного ядра.
12.3. Распределение скоростей во внешней зоне турбулентного ядра
Согласно принятой схеме распределения турбулентной вязкости nТ во внешней части турбулентного ядра, где nТ = k u* АL, исходное выражение для определения распределения осредненных скоростей в этой зоне (2.4) примет вид:
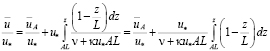 . (12.5)
. (12.5)
Взятие интеграла приводит к зависимости [9]:
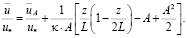 (12.6)
(12.6)
Во внешней зоне турбулентного ядра в качестве линейного масштаба присутствует лишь геометрический масштаб L, а сама формула свидетельствует о том, что распределение осредненных скоростей является параболическим. На большую вероятность такого результата указывали И.О. Хинце, Конт-Белло и др.
При полном разрушении пристенного слоя выступами шероховатости наступает зона квадратичного сопротивления, что сопровождается равенством скорости на высоте выступа шероховатости некоторому значению uΔ. Оно часто принимается равным «второй константе турбулентности», то есть
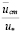 =
= 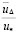 = 8,5. (12.7)
= 8,5. (12.7)
13. Обобщённая формула для расчёта распределения осреднённых скоростей в простейших канонических течениях жидкости
В [9] получена единая формула для расчета распределения осредненных скоростей, которая в указанных выше случаях имеет вид:
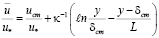 ,
,
при δст ≤ у ≤ A·L; (13.1)
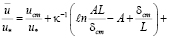
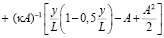 ,
,
при у >A; (13.2)
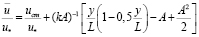 ,
,
при δст = A·L, (13.3)
где 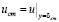 .
.
В приведенных формулах у отсчитывается внутрь потока от стенки, как это было введено И. Никурадзе и Л. Прандтлем. Пределы интегрирования основного уравнения равномерного движения принимались от 0 до у – при гладких и от Δ до у – при шероховатых стенках.
Распределение скоростей в пристенном слое, то есть при 0 ≤ у ≤ δст, получено и представлено в универсальной табличной форме. Формула апробирована на обширных экспериментальных данных.
Формула распространена на всю область сопротивлений. Простейший анализ формул (13.1), (13.2) и (13.3) приводит к выводу о том, что распределение скоростей зависит от трех параметров: δст, А, а, где третий параметр а входит в выражение для δст:
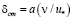 , (13.4)
, (13.4)
где 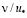 – внутренний линейный масштаб.
– внутренний линейный масштаб.
Оказалось, что δст и а взаимозависимы, поэтому число независимых параметров сокращается до двух. Легко получить дополнительное соотношение для δст:
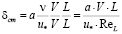 . (13.5)
. (13.5)
Отсюда следует, что, так как предельная толщина пристенного слоя не может превышать характерной толщины потока L, то параметр а не может превышать некоторого значения
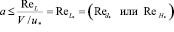 ,(13.6)
,(13.6)
где 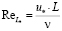 .
.
В противном случае пристенный слой занимает все сечение потока (δст = L) или является недоразвитым (δст > L).
При гладких стенках параметры δст, а и А могут быть функциями лишь числа Рейнольдса.
При шероховатых стенках те же параметры могут определяться лишь относительной шероховатостью Δ/L.
Логично предположить, что если это так, то в зоне доквадратичного сопротивления те же параметры должны зависеть как от ReL, так и от Δ/L.
14. Условия, удовлетворяемые новой формулой для расчёта распределения осреднённых скоростей в простейших канонических течениях жидкости
Выше была изложена методика получения универсальной формулы для расчета распределения осредненных скоростей в продольно однородных потоках. Она базировалась на предварительном обосновании существования вблизи гладких поверхностей тончайшего слоя, в пределах которого вихревая вязкость является отрицательной. С учетом этого обстоятельства была осуществлена схематизация распределения вихревой вязкости по поперечному сечению потока с использованием имеющихся экспериментальных данных.
В свою очередь, принятая схематизация распределения вихревой вязкости позволила разделить турбулентный поток на пристенный слой, толщиной dст, и турбулентное ядро.
Итак, на основе новой модели турбулентности, исходя из перечисленных условий и требований к формуле для распределения осредненных скоростей в продольно-однородных турбулентных потоках, предложены соответствующие формулы, лучше удовлетворяющие указанным условиям, в том числе у стенки и на оси трубы (или свободной поверхности). Каковы эти условия?
1. Как было показано, понятие о длине пути смешения, введенное Л. Прандтлем, не имеет места. Длина, входящая в размерность кинематической турбулентной вязкости nТ, представляет собой просто расстояние от стенки (как это первоначально и было предположено Л.Д. Ландау [16], сменивший по каким-то причинам эту точку зрения на прандтлевскую).
2. У гладкой стенки ламинарный пограничный слой отсутствует.
3. У гладкой стенки существует тончайший слой, в пределах которого nТ отрицательно, что означает, что в пределах этого слоя толщиной
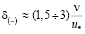
кинетическая энергия турбулентности возвращается осредненному движению. Последнее приводит к некоторому локальному увеличению осредненных скоростей, нарушению линейности в распределении скоростей в этом слое и образованию двух точек перегиба в эпюре скоростей.
4. Универсальная константа Кармана принимается таковой и равной k = 0,4.
5. Влияние шероховатости учитывается эквивалентной шероховатостью Δэ.
6. Градиенты осредненных скоростей у стенки равны 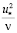 , а на оси трубы или у свободной поверхности являются нулевыми.
, а на оси трубы или у свободной поверхности являются нулевыми.
7. У стенки образуется пристенный слой, толщиной δст = а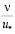 . При больших числах Red оказалось, что а = 70. Это соответствует многим и многим рекомендациям.
. При больших числах Red оказалось, что а = 70. Это соответствует многим и многим рекомендациям.
8. В пределах пристенного слоя сказывается влияние физической n и турбулентной nТ вязкости. Характер этого влияния задается феноменологически с учетом очевидных соображений, – ближе к стенке влияние n должно быть преобладающим, а ближе к условной границе пристенного слоя оно должно становиться исчезающим.
9. В единицах длины, равных 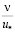 , обозначим толщину слоя с nТ < 0 d(–) = с
, обозначим толщину слоя с nТ < 0 d(–) = с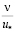 ; толщину слоя с возрастающим влиянием νТ > 0 при
; толщину слоя с возрастающим влиянием νТ > 0 при 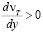 и
и 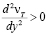 обозначим
обозначим 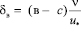 , а толщину верхней части пристенного слоя, на границе которого влияние nТ становится подавляющим при νТ > 0,
, а толщину верхней части пристенного слоя, на границе которого влияние nТ становится подавляющим при νТ > 0, 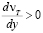 и
и 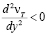 , обозначим δа = (а – в)
, обозначим δа = (а – в)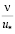 . При больших числах Red рекомендуется принимать а = 70, b = 30, c = 1,5, то есть
. При больших числах Red рекомендуется принимать а = 70, b = 30, c = 1,5, то есть
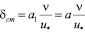 .
.
10. При малых числах Red толщина пристенного слоя становится соизмеримой с rо, что подлежит специальному учету.
11. Турбулентное ядро условно делится в соответствии со схематизацией эпюры распределения турбулентной вязкости νТ = νТ(y) или νТ = νТ(z) на две части. В примыкающей к пристенному слою, где принято, что νТ = k u* y (или k u* z), эпюра распределения осредненных скоростей естественным образом становится логарифмической, а в остальной части, где принято νТ = const, – параболической. Эти части эпюры смыкаются с обеспечением непрерывности в распределении 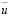 и
и 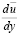 . Первая часть простирается от стенки на расстояние yA = A·rо (или zA = АН), причем при больших Red А = 0,1735.
. Первая часть простирается от стенки на расстояние yA = A·rо (или zA = АН), причем при больших Red А = 0,1735.
12. Числовые значения а, А согласуются со многими опытными данными, хотя и находились определенным образом численно. Мнение о возможности представления эпюры скоростей комбинацией логарифмического и параболического законов высказывалось многократно.
13. Таким образом, при гладких стенках пристенная зона оказывается расчлененной на три части, а турбулентное ядро – на две. Следовательно, эту модель можно назвать пятислойной.
14. Вопреки устойчиво сохраняющемуся мнению многих исследователей, показано, что переход от гладкостенного к доквадратичному сопротивлению связан с разрушением слоя с nТ < 0, что происходит при высоте выступов шероховатости Δэ » 0,2÷0,3δ(–). Переход же от доквадратичного к квадратичному сопротивлению наблюдается при достижении значений Dэ » 0,2÷0,3δст. Это обстоятельство представляется физически более реальным, чем «протыкание выступами шероховатости» ламинарной пленки.
15. Предлагаемые формулы получены интегрированием исходного уравнения
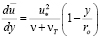
или 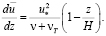
В пределах пристенного слоя, то есть при изменении δ ст. > y >0, интегрирование велось численно, а при r0 > y > δст – аналитически.
16. При шероховатых стенках интегрирование осуществлялось аналитически в пределах Δ < y ≤ rо с принятием в качестве граничного условия значения 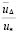 = 8,5 (вторая константа турбулентности).
= 8,5 (вторая константа турбулентности).
17. Оказалось, что наличие у гладкой стенки тонкого слоя, в котором вихревая (турбулентная ) вязкость принимает отрицательное значение, то есть в котором течение является контрградиентным, приводит к образованию точек перегиба на эпюре распределения осреднённых скоростей в продольно- однородных потоках. Как известно, наличие таких точек является мощным фактором, обусловливающим дестабилизацию течения. Само это обстоятельство известно со времён Релея [54], однако поиск этих точек до сих пор не увенчался успехом. Авторы полагают, что причиной этому является практически всеобщее ( за очень малым исключением ) отрицание возможности развития контрградиентных течений в продольно- однородных потоках.
18. Обращаюсь к читателям с просьбой подвергнуть предложенный универсальный метод расчёта распределения осреднённых скоростей в круглых трубах, плоских потоках и пограничных слоях при нулевом градиенте давления широкой проверке с привлечением новейших экспериментальных данных.
Заключение
В данной обзорной статье рассмотрены основные этапы и достижения при решении важной гидравлической задачи о расчёте распределения осреднённых скоростей в продольно – однородных турбулентных потоках. Кратко изложены результаты исследований как возникавшие в начальный период развития подходов к решению проблемы, так и современные достижения в этой области, принадлежащие, в основном, европейским учёным.
По мнению автора, статья будет полезна, как исследователям и преподавателям, так и магистрантам и аспирантам при работе над выпускными работами и диссертациями.


 science-review.ru
science-review.ru
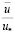 I
I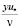 = с·0,1·I
= с·0,1·I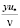 = с+(b – c) 0,1·I
= с+(b – c) 0,1·I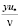 = b + (a – b)0,1•I
= b + (a – b)0,1•I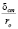 )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
)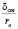 )
)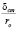 )
)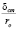 )
)