Задача определения вычетов функций в особых точках актуальна сама по себе, кроме того, её решение ведет к вычислению криволинейных интегралов по замкнутому контуру. Будем рассматривать функции комплексного переменного, у которых в качестве особенностей выступают только конечные полюсы, и искать вычеты функций в этих полюсах.
Вычет функции в любой конечной изолированной особой точке равен коэффициенту С-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки [1], т.е. при 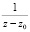 для z0, принадлежащей области комплексных чисел:
для z0, принадлежащей области комплексных чисел: 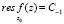 . По теореме Лорана [2, 3] о разложении аналитической функции в кольце в ряд по целым степеням имеет место равенство
. По теореме Лорана [2, 3] о разложении аналитической функции в кольце в ряд по целым степеням имеет место равенство 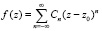 .
.
Поскольку рассматриваются функции, имеющие в качестве особенностей только полюсы z0, то в выколотой окрестности точки z0 ряд Лорана функции f(z) содержит конечное число членов с отрицательными степенями [4]. То есть, если z0 – полюс n-го порядка, то
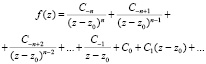
Задача состоит в программном вычислении коэффициента С-1. Очевидны соотношения
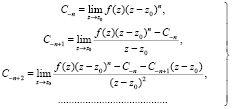 (*)
(*)
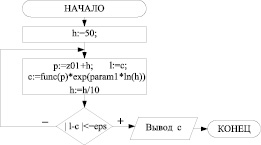
Рис. 1. Структурная схема алгоритма нахождения коэффициентов ряда Лорана с использованием предельного перехода
Последовательное вычисление всех отрицательных коэффициентов ряда Лорана рекуррентно приведет к нахождению С-1. Реализацию предельного перехода алгоритмически предполагалось [5] осуществить следующим образом (рис. 1).
В данном алгоритме используются следующие обозначения: z01 – полюс исходной функции func(z), переменная param1 определяет порядок полюса z01, eps – наперед заданная погрешность вычислений.
Однако таким образом можно точно вычислить лишь коэффициент ряда Лорана с наименьшей отрицательной степенью С-param1. Вычисление следующего коэффициента таким же образом (заменяя лишь выражение для переменной С на выражение, определяющее С-param1+1) дает шесть верных цифр после десятичной точки. Каждый последующий коэффициент вычисляется с большей погрешностью, чем предыдущий; ошибка накапливается, в результате оказывается невозможным точно вычислить вычет функций в полюсах, порядок которых выше второго.
С целью преодоления возникшей трудности предлагается алгоритм приближенного нахождения коэффициентов ряда Лорана, базирующийся на использовании сортировки:
1. На основе сортировки [6, 7], по изложенной в [8, 9] схеме вычисления полюсов комплексных функций находятся все полюсы z0 функции f(z), а также их порядок n [10, 11].
2. Для определения вычета функции в первом из найденных полюсов zk порядка k1 вычисляются необходимые коэффициенты 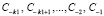 из (*) при повторном применении схемы вычисления полюсов исходной функции (уже без учета порядка) в месте спуска к наименьшему значению в окрестности локализованной точки при достаточном сужении области поиска вокруг уже определенного полюса. Иными словами, искомые коэффициенты вычисляются по данной схеме непосредственно по виду выражений, стоящих под знаком предела из (*), по ходу циклического приближения значения z к заново вычисляемому значению z0.
из (*) при повторном применении схемы вычисления полюсов исходной функции (уже без учета порядка) в месте спуска к наименьшему значению в окрестности локализованной точки при достаточном сужении области поиска вокруг уже определенного полюса. Иными словами, искомые коэффициенты вычисляются по данной схеме непосредственно по виду выражений, стоящих под знаком предела из (*), по ходу циклического приближения значения z к заново вычисляемому значению z0.
3. Пункт 2 повторяется для каждого из найденных полюсов, пока не будет определен вычет во всех полюсах.
Программная реализация пункта 2 опирается на алгоритм, представленный на рис. 2.
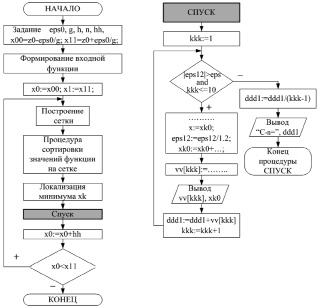
Рис. 2. Упрощенная структурная схема алгоритма приближенного вычисления коэффициента ряда Лорана в окрестности точки z = z0
Как отмечалось выше, область поиска полюсов нужно ограничить небольшой окрестностью вокруг уже известного полюса, что и отражено в блоке описания констант:
eps0 = zz*g; x00 = z0-eps0/g; x11 = z0 + eps0/g.
В ходе численного эксперимента было установлено, что численные значения константы eps0 и граничных точек окрестности поиска x00, x11 зависят друг от друга. Эту зависимость определяет коэффициент g, введенный в блоке описания констант. Значение коэффициента g может быть варьировано в рамках значений от 10-424 до 10-9, что не влияет на точность результата и позволяет произвольно сужать или расширять окрестность поиска.
Значение множителя zz константы eps0 подобрано эвристически в ходе численного эксперимента, оно варьируется в зависимости от порядка полюсов. Однако выбранные значения zz, приведенные в каждом случае в примере 1, остаются постоянными для различных функций, которые имеют одинаковый порядок полюсов.
Приближения к коэффициенту ряда Лорана, который вычисляется по соответствующим формулам из (*), запоминаются в массиве vv, после чего искомый коэффициент представляется как среднее арифметическое значений первых десяти элементов этого массива.
Замечание. Заметим, что весовой одночлен является необходимой компонентой для вычисления порядка полюсов функций в случае отсутствия информации о количестве полюсов, поскольку возможен случай единственности полюса. Отсутствие весовой функции может повлиять на правильность определения порядка полюса, но никак не на само значение полюса. Поэтому использование весового одночлена является излишним при вычислении вычетов функции в полюсах.
Описанный метод ниже иллюстрируется на примере.
Пример. Вычислить вычет функции 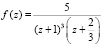 в полюсе, имеющем порядок, отличный от 1.
в полюсе, имеющем порядок, отличный от 1.
Отметим, что представление исходной функции в таком виде, когда обратная к ней задана разложением на множители, используется с целью иллюстрации, для сравнения результатов работы программы с очевидными значениями полюсов. Исходная функция может быть представлена в виде любой дробно-рациональной функции.
Определим все полюсы исходной функции и их порядок. Как и прежде, изменения произойдут лишь в блоке описания констант и функций:
На вход программы, полный текст которой представлен в [5], подается функция, нули которой совпадают с полюсами исходной функции f(z), она получена при помощи простейших алгебраических преобразований обратной функции к f(z) к виду
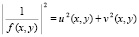 ,
,
где
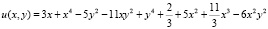 ,
,
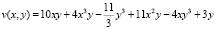 .
.
В качестве весовой используется произвольно выбранная функция 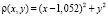 .
.
Результаты работы программы приведены в таблице.
Результаты вычисления полюсов функции 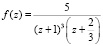 с учетом их порядка
с учетом их порядка
|
Действительная часть полюса |
Мнимая часть полюса |
Порядок полюса |
Значение обратной функции |
|
–1.00E+0000 –6.66E-0001 |
1.05E-1332 1.05E-1332 |
3 1 |
0.00E+0000 0.00E+0000 |
Мнимая часть полученных полюсов настолько мала (порядка 10–1332), что будем считать ее нулем и далее возможно использовать программу вычисления действительных нулей функций из [12, 13].
По условию задачи, необходимо вычислить вычет функции f(z) в первом полюсе z = –1. Данный полюс имеет порядок 3, поэтому коэффициенты ряда Лорана имеют следующий вид:
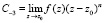 ,
, 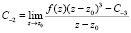 ,
,
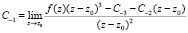 .
.
Фрагмент листинга программы на языке Pascal [14, 15] для вычисления коэффициента C-3 – раздела описания констант и функций и спуска к наименьшему значению в окрестности локализованной точки:
…………………….
const eps=1.1e-444; g=1e-19; eps0=1e-18*g;
h=eps0/(2*1024/20); n=1024; nn=trunc(n/2); hh=n*h; tt=64; np=4;
{область поиска полюсов}
x00= -1-eps0/g ; x11=-1+eps0/g; ………………………………….
kkk:=1;
{Вычисление коэффициентов Лорана одновременно при спуске}
{к наименьшему значению в окрестности локализованной точки}
while (abs(eps12) > eps) and (kkk<=10) do begin x:=xk0;
minx(x,min,ee); eps12:=eps12/1.2; xk0:=xk0+ee*hx-eps12; vv[kkk]:=sqr(xk0+1)*(xk0+1)*f(xk0);
Writeln ('C(-n)=',vv[kkk],' ',xk0,' ',func(xk0,korx,r,param));
ddd1:=ddd1+vv[kkk]; kkk:=kkk+1; end; ddd1:=ddd1/(kkk-1); writeln ('!!!!!C(-n)=',ddd1);
eps13:=eps0/1.2; x:=xk0+ee*hx+eps12; xk1:=xk1+eps12;end; ……………………………
Результат работы программы:
C<-n>=-1.50000000000000E+0000.
Вычисленные коэффициенты C-3 заносятся в массив vv, на выходе программы представлено среднее арифметическое значений первых десяти элементов этого массива. Значение C-3 для функции f(z) вычислено «абсолютно» точно (с точностью до формата представления выводимых значений). Как показал численный эксперимент, коэффициент с наименьшей отрицательной степенью всегда удается вычислить с такой точностью.
Для вычисления коэффициента C-2 ряда Лорана функции f(z) необходимо в блоке описания констант положить eps0=1e-10*g и заменить фрагмент программы, в котором осуществляется вычисление коэффициентов Лорана одновременно при спуске к наименьшему значению в окрестности локализованной точки:
while (abs(eps12) > eps) and (kkk<=10) do begin x:=xk0; minx(x,min,ee);
eps12:=eps12/1.2; xk0:=xk0+ee*hx-eps12; vvv[kkk]:= (sqr(xk0+1)*(xk0+1)*f(xk0)+15)/(xk0+1);
Writeln ('C(-n+1)=',vvv[kkk],' ', xk0,' ',func(xk0,korx,r,param));
ddd2:=ddd2+vvv[kkk]; kkk:=kkk+1; end; ddd2:=ddd2/(kkk-1); writeln ('!!!!!C(-n+1)=',ddd2);
Результат работы программы:
C<-n+1>=-4.49999999783160E+0001.
Этот результат можно считать вычисленным сравнительно точным (по сравнению с C-2 = –45).
Численный эксперимент показал, что для наиболее точного вычисления последнего коэффициента C-1 изменения следует внести в блок описания констант: eps0=1e-5*g, а фрагмент, в котором осуществляется вычисление коэффициентов Лорана одновременно при спуске к наименьшему значению в окрестности локализованной точки изменить на
while (abs(eps12) > eps) and (kkk<=10) do begin x:=xk0; minx(x,min,ee);
eps12:=eps12/1.2; xk0:=xk0+ee*hx-eps12;
vvv[kkk]:=(sqr(xk0+1)*(xk0+1)*f(xk0)+15+44.9999999783160*(xk0+1))/sqr(xk0+1);
Writeln ('C(-n+2)=',vvv[kkk],' ', xk0,' ',func(xk0,korx,r,param));
ddd2:=ddd2+vvv[kkk]; kkk:=kkk+1; end; ddd2:=ddd2/(kkk-1);
writeln ('!!!!!C(-n+2)=',ddd2); goto 777;
Результат работы программы:
C<-n+2>=-1.34993781725914E+0002.
Приближение этого значения к истинному (C-1 = –135) достаточно грубое – с точностью до 10–2. Увеличить точность вычисления вычета C-1 в этом варианте метода не удалось. А поскольку чем выше порядок полюса, тем большая погрешность вычислений будет накапливаться, данным способом можно вычислить вычеты функций в точках полюсов с порядком не выше третьего.
Значения коэффициентов ряда Лорана, вычисленных фактически без погрешности, можно получить, реализовав следующий алгоритм.
1. Определяются все полюсы zk функции f(z) с учетом их порядка на основе изложенного метода.
2. Для определения вычета функции в первом из найденных полюсов z0 порядка n точно вычисляется коэффициент ряда Лорана C-n с наименьшей отрицательной степенью способом, описанным выше.
3. Для вычисления коэффициентов C-n+k (где 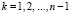 ) формируется функция
) формируется функция
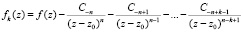 ,
,
правая часть которой поступает в блок формирования входной функции только после предварительного преобразования ее к виду неприводимой рациональной дроби.
4. Пункты 2–3 повторяются для всех найденных полюсов до тех пор, пока не будет установлен вычет в каждом полюсе.
Описанный способ нахождения коэффициентов ряда Лорана и, на его основе, вычетов функции в полюсах представляется наиболее рациональным, несмотря на алгебраические преобразования, так как он позволяет получить точный результат, помимо этого, существенна возможность программной реализации этих преобразований ввиду их простоты. Рекуррентное вычисление последующих коэффициентов ряда Лорана через предыдущие описанным способом с априори заданной точностью позволяет определить необходимое количество коэффициентов при отрицательных степенях ряда Лорана.
Работа выполнена при финансовой поддержке РФФИ (проект 16-07-00100).


 science-review.ru
science-review.ru