Scientific journal

Scientific Review. Technical science

ISSN 2500-0799

ПИ №ФС77-57440

Предлагаются алгоритмы для определения по индексам входных данных экстремальных значений норм решений систем ОДУ. Схема модифицируется для поиска экстремумов норм [1, 2] преобразованных разностных решений систем уравнений при вариации параметров. Анализируется экстремальное отклонение решения системы от устойчивого состояния, и на основе этих данных алгоритмы применимы к оценке устойчивости, в частности при возмущении параметров.

Вычисление экстремальных значений функции двух действительных переменных

В начале рассматривается функция одной действительной переменной y = f(x). Пусть функция определена и задана на промежутке 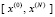. На сетке считываются значения функции f(x), , .

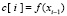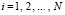Значения c[i] сортируются. Процедура сортировки в программе обозначена как sort [3, 4]. К выходу процедуры сортировки подсоединяется специально сконструированный оператор: ,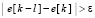
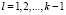. С помощью данного оператора производится автоматическая идентификация каждого минимума в промежутке ε среди элементов c[i].

Смысл условия в том, что в ε-промежутках входных значений функции с индексом e[k] нет значений уже в отсортированном массиве c1, больших по значению, чем элемент с индексом [5]. Это значит, что значение функции y в узле 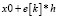не превосходит значений во всех точках заданной ε-окрестности.

Если оператор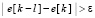
заменить на другой оператор, с помощью которого локализуется максимум 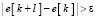, , 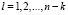то осуществляется вычисление максимумов функции.

Изложенная схема применяется для вычисления всех экстремумов функции двух переменных 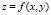[6]. Задаются границы 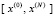и ,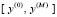
где строится область: ,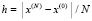
, , , .

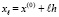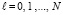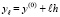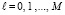Для нахождения минимумов функции 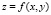перебираются значения вдоль j-го столбца по ординате OY, в результате чего находится наименьшее по строкам значение 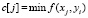, , 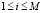которое поступает на вход сортировки с индексом j.

После реализации сортировки подсоединяется представленный выше оператор, с помощью которого локализуется минимум.

Оператор для текущего узла e[k] находит каждый узел 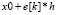, в проекции ε, на абсциссу OX среди которых нет точек, предшествующим значениям в отсортированном массиве.

Значение точки минимума 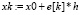фиксируется, после чего локализуется ордината, в которой вычисляется приближенное минимальное значение функции двух действительных переменных.

Представленная схема позволяет программно вычислять экстремумы произвольной функции рассматриваемого вида. Алгоритм может использоваться для идентификации экстремумов функций нескольких переменных [7].

Решение нелинейных систем уравнений

Схема применяется к приближенному решению систем нелинейных уравнений. Пусть исходная система преобразована к виду 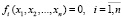, где левые части являются функциями от n действительных переменных. Совокупность функций 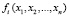образует n-мерную вектор-функцию аргументов 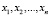. Пусть требуется приближенно найти все решения системы 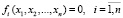в заданной области , , …,
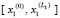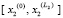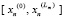. Строится сетка 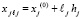, , 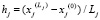, 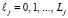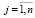. Во всех ее узлах вычисляются значения нормы 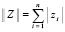рассматриваемой функции, которые принимаются за элементы n-мерного массива: ,
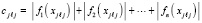где индексы соответствуют узлам многомерной сетки. Левая часть 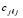интерпретируется как дискретная функция n переменных, ее минимумы можно идентифицировать программно по изложенной схеме.

Пример. Приближенное решение системы

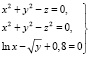
в области 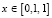, , 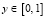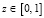вычисляется по программе Program UravnNelin, представленной в листинге [2]:

label 21,22,23; const eps0=0.1; h=eps0/23; x00=0.1;

x11=1; y00=0; y11=1; z00=0; z11=1;

n00=trunc(6/h); nn=n00+round(n00/2)+1;

type vect1=array [1..2*nn+nn] of double;

vect2=array [1..2*nn+nn] of longint;

var i,j,k,k1,r,rx,ry,rz,nn0,kx,ky,kz : integer;

c,a1,az: vect1; e, ex, ey,ez: vect2;

x,x0,x1,xk,minx,minz: double;

y,y0,y1,yk,z0,z1,z,zk: double;

function ff1 (x,y,z: double): double;

begin ff1:= x*x+y*y-z ; end;

function ff2 (x,y,z: double): double;

begin ff2:= x*x+y*y-z*z; end;

function ff3 (x,y,z:double): double ;

begin ff3:= ln(x)-sqrt(y)+0.8; end;

function func (x,y,z: double): extended;

var p: double; i1: integer;begin

func:= abs(ff1(x,y,z))+abs(ff2(x,y,z))+abs(ff3(x,y,z)); end;

procedure minyz (var x,y,z,minx: double);

begin minx:=func(x,y,z); i:=1;

while i<= trunc((y11-y00)/h) do begin

j:=1; while j<= trunc((z11-z00)/h) do

begin y:=y0+i*h; z:=z0+j*h;

IF minx > func(x,y,z) then minx:=func(x,y,z);

j:=j+1; end; i:=i+1; end; end;

procedure minyy (var x,y,z,minz:extended);

begin minz:=func(x,y,z); i:=1;

while i<=trunc((y11-y00)/h) do begin

begin y:=y0+i*h; if minz > func(x,y,z) then

minz:=func(x,y,z) end; i:=i+1;end; end;

procedure sort(var nn0:

longint; var c: vect1; var e: vect2);

{ Oписание процедуры sort }

begin x0:=x00; x1:=x11;

y0:=y00; y1:=y11;z0:=z00; z1:=z11; nn0:=n00;

for rx:=1 to nn0 do begin

x:=x0+rx*h; minyz (x,y,z,minx); a1[rx]:=minx; end;

sort( nn0, a1, ex); kx:=1;

while kx<= nn0 do begin

for rx := 1 to kx-1 do

IF abs( ex[kx]-ex[kx-rx] ) <= eps0/h then goto 21;

xk:= x0+ex[kx]*h; for rz:=1 to nn0 do begin

z:=z0+rz*h; x:=xk;

minyy (x,y,z,minz); az[rz]:=minz; end;

sort( nn0, az, ez); kz:=1;

while kz<= nn0 do begin

for rz := 1 to kz-1 do

IF abs(ez[kz]-ez[kz-rz]) <=eps0/h then goto 22;

zk:= z0+ez[kz]*h;

for ry:=1 to nn0 do begin

y:=y0+ry*h; a1[ry]:=func(xk,y,zk) end;

sort( nn0, a1, ey); ky:=1;

while ky<= nn0 do begin

for ry := 1 to ky-1 do

IF abs(ey[ky]-ey[ky-ry]) <=eps0/h then goto 23;

yk:= y0+ey[ky]*h;

writeln (' ', xk,' ');

writeln (' ', yk,' ');

writeln ( zk,' ', ff1(xk,yk,zk):3:5,' ',ff2(xk,yk,zk):3:5,'',ff3(xk,yk,zk):3:5);

23: ky:=ky+1; end;

22: kz:=kz+1; end;

21: kx:=kx+1; end; end.

Результат вычислений:

Представленный алгоритм может использоваться для решения трансцендентных уравнений [2] и по способу построения отличается от аналогов [8–10].

Идентификация экстремумов и нулей разностных решений систем ОДУ

Пусть рассматривается задача Коши для уравнения

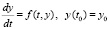(1)

и выполняются условия существования и единственности решения. Для решения (1) с малым шагом h на промежутке 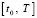используется метод Эйлера:

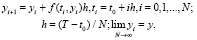(2)

Разностные значения из (2) рассматриваются как элементы массива

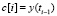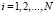, . (3)

После сортировки массива (3) применяется оператор локализации экстремумов. Схема локализации экстремальных элементов в массиве (3) такая же, как и для массива (1) функции одной переменной, за исключением того, что в случае разностной схемы нельзя выполнить спуск. Погрешность вычисления экстремумов решения уравнения (1) полностью определяется погрешностью разностного приближения. С точностью до этой оговорки имеют место устойчивость локализации и вычисления экстремумов решения (2) [11, 12].

Для поиска нулей достаточно взять модули значений (3) и среди их минимумов выбрать близкие к нулю. Как и в случае функции одной переменной, необходимо смещение текущего отрезка по всему промежутку поиска экстремумов с дополнительной проверкой границ смещаемого отрезка на экстремум.

Схема без принципиальных изменений переносится на случай двух и более уравнений путем ее буквального повторения для каждого уравнения в отдельности. Предполагается, что для задачи Коши [13]

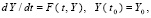(4)

где

,

,

,

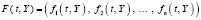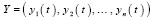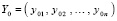выполнены все условия существования и единственности, а также, что имеет место сходимость к решению рассматриваемого разностного метода на отрезке 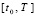. На вход сортировки подаются разностные приближения каждой компоненты решения:

.

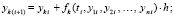
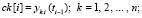
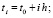
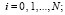
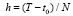На выходе метода идентифицируются все локальные экстремумы каждой переменной yk, в виде последовательности ck[i], в окрестностях малого промежутка на всем отрезке .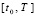

Нули разностных приближений компонент получатся, если на вход подавать модули значений 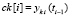с оценкой на выходе малости минимумов. По-прежнему необходимо смещение текущего отрезка по всему промежутку поиска экстремумов с проверкой границ смещаемого отрезка на экстремум. Вместо метода Эйлера могут применяться разностные методы высшего порядка [14], численный эксперимент показывает возможность идентификации экстремумов с точностью до формата представления данных в языке программирования.

Под устойчивостью понимается устойчивость по Ляпунову [1]. Пусть рассматривается система нелинейных ОДУ:

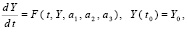
где 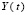определяются по методу Эйлера, 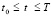; 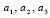– варьируемые числовые параметры в диапазоне , , .
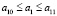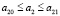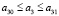Возмущенные начальные данные обозначаются 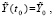соответственное им возмущенное решение записывается в виде 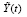. Требуется найти все экстремальные отклонения от нуля нормы разности между возмущенным и невозмущенным решениями системы dY/dt при вариации числовых параметров.

Способ оценки отклонений опирается на схему идентификации экстремумов [4] дискретно представленных функций четырех действительных переменных. На вход алгоритма подается функция одной независимой переменной t, роль трех других играют варьируемые параметры. Роль функции играет норма разности вычисляемых по разностной схеме значений вектор-функций 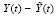. При выборе нормы:

,

.

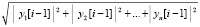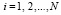На вход метода поступает

,

.

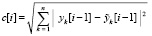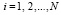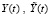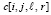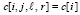При этом решения вычисляются по разностной схеме отдельно для каждого набора дискретизированных значений трех варьируемых параметров. Выбранные дискретизированные значения левой части c[i] задают трехмерный массив, к которому добавляется еще одно измерение по независимой переменной t. Получится четырехмерный массив с элементами , где из 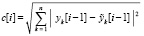, i = 1, 2, ..., N
при значениях параметров ,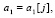
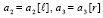, индексы которых указывают номера шагов дискретизации.

Найденные экстремумы характеризуют меру отклонения возмущенного решения от невозмущенного (меру возмущения решения). Значение глобального максимума позволит найти наибольшее значение возмущения на отрезке 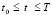при всех дискретных значениях трех параметров.

Соответственные программы приводятся в [2, 6]. В [2] детально изложено применение подхода к анализу возмущений энергетических систем при возмущении параметров. Изложенный метод применяется к оценке устойчивости на основе анализа поиска нулей характеристического полинома. Для системы [2] характеристическое уравнение имеет вид 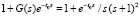или .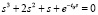

Нули полинома и трансцендентной функции в левой части последнего уравнения можно найти как минимум модуля функции 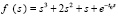при вариации параметра 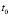. Данный метод переносится на поиск решений систем нелинейных уравнений, которые могут содержать трансцендентные функции, при этом вместо минимума модуля ищется минимум нормы компонент зависимых переменных на многомерной сетке.

Заключение

С помощью оптимизационного алгоритма осуществляется оценка экстремального отклонения системы от ее устойчивого состояния при вариации параметров. Особенностями предложенного метода являются его построение на основе сортировки, автоматичность программной локализации экстремальных значений разностных решений, схема может иметь произвольные размеры поиска экстремумов в области определения.

Работа выполнена при финансовой поддержке РФФИ (проект 16-07-00100).