science-review.ru
Получение трехмерной формы объекта по его изображениям с различных ракурсов является перспективным способом быстрого и качественного построения 3D моделей, которой можно найти множество различных областей применения [1–4].
Реконструкция трехмерных объектов по изображениям – это процесс получения 3D-модели объекта по набору его изображений, выполненных с различных ракурсов. В данной статье предлагается модель решения задачи реконструкции. Рассматриваемая модель представляет собой многослойную нейронную сеть, в основе которой лежит рекуррентная LSTM сеть.
Архитектура нейронной сети
для реконструкции трехмерных сцен
Для решения задачи реконструкции трехмерных сцен используется нейронная сеть. Входными данными для нейронной сети является набор изображений трехмерного объекта с различных ракурсов. Выходом нейронной сети будет являться трехмерная модель.
Нейронная сеть состоит из трех основных компонентов:
- сверточная нейронная сеть для 2D изображений (Кодирующая нейронная сеть) [5, 6];
- рекуррентная Long Short Term Memory (LSTM) нейронная сеть [7–9];
- декодирующая нейронная сеть на основе сверточной архитектуры [5].
Принимая на вход одно или несколько изображений объекта с произвольных ракурсов, сверточная нейронная сеть сначала кодирует каждое входное изображение x в вектор низкой размерности τ(x). Затем данный кодированный вектор передается на полносвязный слой. Выход полносвязного слоя соединен со входом рекуррентной LSTM нейронной сети, которая обновляет внутреннее состояние ячеек. На последнем этапе декодирующая нейронная сеть декодирует скрытые состояния блоков LSTM и генерирует трехмерную воксельную реконструкцию. Общая схема модели приведена на рис. 1.
Кодирующая сверточная нейронная сеть
Для преобразования изображения в вектор атрибутов используется многослойная сверточная нейронная сеть, структура которой изображена на рис. 2.
На вход подается RGB изображение размером 127x127 пикселей. Нейронная сеть состоит из 6 стандартных сверточных слоев. После каждого слоя свертки идет субдискретизирующий слой. В качестве функции активации для сверточных слоев используется линейный выпрямитель с утечкой (Leaky Rectified Linear Unit), который задается следующим образом:
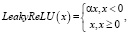
где α – малая константа.
Выход кодирующей сети передается на вход полносвязного слоя, который сжимает выходное значение до вектора атрибутов τ размерностью 1024.
Рекуррентная LSTM нейронная сеть
Центральной частью реконструкции является рекуррентная нейронная сеть, которая позволяет модели «запомнить» ту часть объекта, которую она уже «видела», и обновлять свою память, когда появляется новые детали объекта.
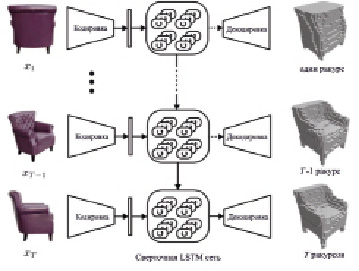
Рис. 1. Схема используемой модели реконструкции
Рис. 2. Кодирующая сверточная нейронная сеть
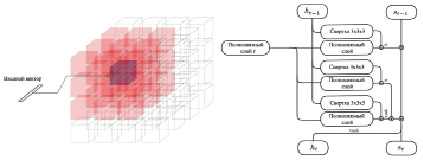
Рис. 3. Структура реконструирующей рекуррентной нейронной сети
Рис. 4. Обновление состояния блоков, отвечающих только за определенный ракурс объекта
Модули LSTM организованы в трехмерную сетку размером 4х4х4. Использование классической архитектуры LSTM для выходного пространства такой большой размерности достаточно сложно. Поэтому используемая нейронная сеть отличается от стандартной LSTM сети применением сверточных слоев (рис. 3). Каждый из модулей сети отвечает за реконструкцию конкретной части конечного объекта.
Каждый модуль имеет независимое скрытое состояние ht(i, j, k) и запоминаемое состояние ct. Для сокращения количества параметров обучения из классического LSTM-блока [9] был убран выходной фильтр. Вместо этого выходное значение сразу передается к следующему блоку без изменений.
,
.
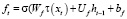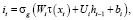
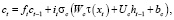
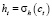Интуитивно такая конфигурация позволяет блоку LSTM-сети обрабатывать несоответствие между конкретным предсказываемым участком реконструкции и моделью реального объекта, так что каждый блок учится восстанавливать одну область пространства воксела вместо того, чтобы реконструировать все пространство (риc. 4).
Кроме того, в классической LSTM сети все модули соединены друг с другом последовательно [9]. Это значит, что на текущее состояние ht оказывают влияние все ht-1 элементы. В используемой архитектуре влияние на скрытое состояние оказывают только элементы, находящиеся по соседству с текущим. Количество соседей определяется размерностью используемого ядра свертки.
Декодирующая нейронная сеть
На последнем этапе используется декодирующая нейронная сеть, задачей которой является преобразование скрытого состояния (размерностью 4х4х4) к более высокому выходному разрешению (32х32х32). Количество слоёв свертки определяется требуемым в результате разрешением трехмерной модели.
Структура декодирующей нейронной сети изображена на рис. 5.
В используемой модели применяется 5 сверточных слоев. После последнего сверточного слоя результат, представляющий собой вектор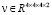 
, преобразуется к трехмерной матрице вероятности занятости вокселем каждой ячейки (i, j, k). Данное преобразование выполняется с помощью функции softmax, применяемой к каждому вокселю:
.
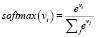При использовании данной функции суммирование ведется по всем нейронам слоя сети. Такой выбор обеспечивает сумму выходов слоя, равную единице при любых значениях входа x и позволяет минимизировать сумму перекрестных энтропий.
Функция потерь нейронной сети
Функция потерь для модели нейронной сети определяется как сумма перекрестных энтропий всех вокселей:
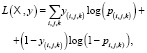
где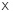 
– множество входных изображений, 
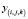– соответствующее истинное значение занятости вокселя, 
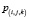– предсказываемая вероятность занятости вокселя.
Реализация
Для реализации модели нейронной сети использовалась библиотека Theano [10]. Для обучения сети использовались 3D модели, на основе которых генерировались входные изображения и выходные сетки вокселей. Все ракурсы выбирались случайно. В качестве входных использовались изображения размером 127х127, размер выходной сетки вокселей – 32х32х32
Исходные 3D модели и их изображения были взяты из базы данных ShapeNet. Набор данных был разделен на два подмножества: 80 % данных использовалось для обучения, 20 % для тестирования сети. Для слоя LeakyReLU использовался коэффициент α, равный 0,1. Для обучения использовался метод стохастического градиентного спуска [5].
Оценка качества реконструкции
На рис. 6 приведены результаты реконструкции для некоторых моделей.
Для оценки качества реконструкции использовались две метрики. В качестве основной использовалась метрика Intersection-over-Union, равная отношению количества вокселей, получаемых при пересечении результата реконструкции с исходной моделью, к количеству вокселей, получаемых при объединении результата с исходной моделью.
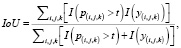
где I – индикаторная функция, t – порог вероятности, при котором считается, что воксель должен быть закрашен,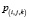 
– вероятность закраски вокселя (результат реконструкции), 
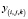– закраска вокселя в исходной модели.
Чем больше значение функции IoU, тем более точная модель была получена в результате реконструкции.
В качестве второй метрики использовалась сумма перекрестных энтропий вокселей:
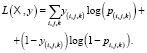
Чем меньше значение данной метрики, тем выше качество реконструкции.
Рис. 5. Декодирующая нейронная сеть
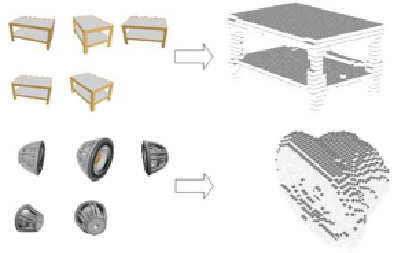
Рис. 6. Результаты реконструкции объектов
Исходная трехмерная модель преобразовывалась к воксельному представлению размером 32х32х32. Затем данная модель сравнивалась с моделью, полученной в ходе реконструкции.
Было проведено сравнение качества реконструкции в зависимости от используемого размера ядра свертки.
Средние результаты для LSTM сети и ядра свертки размером 1x1x1 и 3x3x3 приведены в таблице.
Результаты оценки качества реконструкции объектов LSTM сетью в зависимости
от размера ядра свертки
|
Ядро свертки |
IoU |
Cумма перекрестных энтропий |
|
1x1x1 |
0,499 |
0,116 |
|
3x3x3 |
0,539 |
0,106 |
Результаты показывают, что для ядра свертки размером 3х3х3 качество реконструкции выше. Использование ядра свертки размером 3х3х3 означает, что соседние рекуррентные блоки соединены между собой, тогда как при использовании ядра свертки размером 1х1х1 значения соседних рекуррентных блоков не учитываются.
Таким образом, была рассмотрена модель реконструкции трехмерных сцен по изображениям с различных ракурсов на основе нейронных сетей LSTM типа. Основным преимуществом использования такой сети является ее способность эффективно обрабатывать самоперекрывающиеся объекты. Если в очередном входном изображении видны детали объекта, которые ранее были перекрыты из-за ракурса съемки, то такая сеть обновит состояния LSTM для ранее невидимых деталей объекта, но при этом состояния других частей объекта остаются прежними. Это позволяет получить достаточно качественную трехмерную модель объекта по небольшому количеству входных изображений, тогда как классические алгоритмы реконструкции [11–13] требуют не менее 10 различных ракурсов для получения качественной реконструкции. Однако, в отличие от классических алгоритмов, при увеличении количества входных изображений увеличение качества реконструкции происходит незначительно.