science-review.ru
Технические комплексы, представляющие собой многосвязные механические системы, широко используются в океанологии. Это касается буксировки надводных и подводных судов, взаимодействия подводных аппаратов и роботов с обеспечивающим судном и ряд других задач, например постановка буйковых станций. Такие комплексы, выполняющие указанные задачи, в самом общем случае можно представить как совокупность абсолютно твердых тел с голономными и неголономными связями. Конфигурация таких систем может быть достаточно сложной, обладающей как структурой дерева, так и кольцевой структурой. Кроме того, при проектировании подводных робототехнических систем существенное значение приобретает компьютерное моделирование поведения исследуемого объекта. Компьютерное моделирование при наличии адекватных натуре математических моделей позволяет в значительной мере сократить сроки и стоимость разработки.
Подходы к исследованию многосвязных механических систем
Обширный класс многосвязных механических систем может быть определен как механическая система двух твердых тел с гибкой связью. С поведением двух тел с гибкой связью в океанической среде связаны такие операции, как установка буйковых станций на течении, буксировка поврежденного судна, буксировка бурильных платформ несколькими буксирами, буксировка над дном океана носителей океанографической аппаратуры и др. Возможные приложения задачи двух тел с гибкой связью в океанологической практике представлены на рис. 1. В зависимости от наличия активных движителей на устройствах, входящих в состав данных систем, весь класс систем можно разделить на три типа: полностью пассивная система, в которой ни одно из двух тел не обладает движителями, активная система, в которой оба тела имеют движители, и система комбинированного типа.
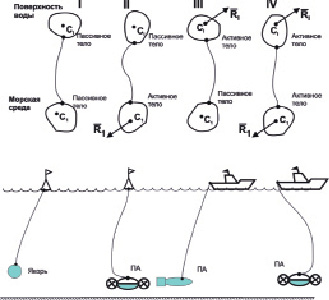
Рис. 1. Буй на плавучем якоре – I; Подводный аппарат с выброшенным на поверхность моря буем связи – II; Буксировка подводного аппарата судном – III; Привязной телеуправляемый подводный аппарат, имеющий связь с обеспечивающим судном через кабель-трос – IV
Механическая система IV принадлежит к активному типу систем, I – к пассивному, а системы II и III – к комбинированному типу. Управляющие силы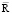 
приложены к центрам инерций – С, активных тел. Целым рядом исследователей велось изучение отдельных элементов, составляющих механическую систему двух тел с гибкой связью в приложении к морской практике. Общеизвестны работы по теории судна, подводных аппаратов. Имеется многочисленная литература, посвященная описанию поведения кабель-троса и др. Различия в исходных предпосылках, математическом аппарате составления моделей не позволяют полностью оценить все многообразие взаимодействий отдельных частей системы. Поэтому представляется целесообразным создание математической модели механической системы двух тел с гибкой связью с единых позиций, на основе аналитической механики многосвязных систем [1, 2].
Анализ подводных робототехнических систем
В обобщенном виде подводную робототехническую систему можно представить как погруженную в жидкость механическую систему твердых тел, имеющую в своем составе гибкие связи. При этом твердыми телами являются надводные и подводные плавсредства (суда, баржи, понтоны, подводные лодки и др.), подводные аппараты (телеуправляемые, буксируемые, автономные) и вспомогательные устройства (заглубители, буи, плавучести, грузы и т.п.). Гибкими связями будут являться цепи, тросы, канаты и т.п. С учетом вышесказанного математическая модель подводных робототехнических систем может строиться в виде дифференциальных уравнений динамики системы твердых тел, с гибкими связями в жидкости.
Прежде всего, следует провести анализ механических структур робототехнических систем. Однако, прежде чем приступить к структурному анализу, необходимо ввести некоторые ограничения на свойства предмета исследования.
Эти ограничения следующие.
Тела, входящие в робототехническую систему, например такие как надводные и подводные плавсредства, подводные аппараты, буи, плавучести, грузы и т.п. объекты, рассматриваются как абсолютно твердые, имеющие в общем случае 6 степеней свободы.
Гибкие связи, например, такие как цепи, тросы, канаты и т.п., рассматриваются как абсолютно гибкие нерастяжимые (идеальные) нити. Под идеальной нерастяжимой гибкой нитью обычно понимают линейный материальный континиум, который может принимать произвольную форму в пространстве. В идеально гибкой нити существует только сила вдоль её касательной (сила натяжения), изгибающий и крутящий моменты отсутствуют. Если физико-механические характеристики гибкой связи не позволяют считать ее идеальной на малой длине, то всегда можно подобрать такую длину, при которой нить становится практически идеальной.
Взаимодействие между телами системы осуществляется только через прямые связи. Считается, что взаимное влияние тел друг на друга через среду мало и поэтому не учитывается.
Как правило, робототехнические системы являются неконсервативными системами, так как в реальных условиях происходит активный энергетический обмен со средой (жидкостью).
Далее следует отметить, что под подводной робототехнической системой мы понимаем связанную механическую систему, состоящую из I твердых тел и J гибких идеальных связей, погруженную в жидкость. Минимальный состав системы включает одно твердое тело (I = 1) и одну гибкую связь (J = 1).
Каждая робототехническая система обладает структурой и конфигурацией. Структура характеризуется количеством твердых тел (узлов) I и гибких связей J, а также способом (или порядком) их объединения в систему. Различают системы с неизменной во времени (I + J = const) и изменяемой структурой (I + J = var). Конфигурация определяет взаимное расположение в пространстве узлов и связей при неизменной структуре. Многообразие конфигураций, принимаемых системой, является пространством конфигураций [3, 4].
Усовершенствование прикладных программ статики тросовых систем
Программа расчета статического равновесия предназначена для определения пространственной конфигурации подводных объектов, содержащих гибкие связи (тросы, буйрепы, кабели и т.п.) – подводных тросовых систем. Традиционными видами подводных тросовых систем являются заякоренные буйковые станции и буксируемые системы.
Любую механическую систему можно условно разделить на отдельные составляющие, примерно разделив их на твердое тело и гибкую связь, в виде цепочки твердых тел с идеальными связями. При таких допущениях эту механическую систему можно рассматривать как систему абсолютно твердых тел с голономными связями. Набор таких механических составляющих представляет собой многомерный объект естественного движения.
Для формализации расчетов подводных тросовых систем такие системы рассматриваются, как системы абсолютно твердых тел с голономными идеальными связями. Гибкая связь при этом аппроксимируется шарнирно-сочлененным многозвенником. Используемый метод расчета основан на определении ориентации каждого тела в отдельности, на базе аксиомы освобождаемости от связи, с учетом граничных условий, с последующей компоновкой в исходную конфигурацию по геометрическим уравнениям связи (структурной матрице), при использовании условий неразрывности. На основе этого метода расчета создано соответствующее программное обеспечение. Разработанный пакет прикладных программ позволяет определять форму и натяжение тросовой системы в вертикальной плоскости для двух классов объектов – буксируемых и заякоренных (закрепленных) систем.
Выполнено усовершенствование пакета программ, через дополнение его информационно-справочной системой и конструктором конфигураций подводных тросовых систем. Экранное изображение одного из элементов информационно-справочной системы приведено на рис. 2 и рис. 3. На рисунках изображены два варианта кабельного круга для буксировки и буйрепов.
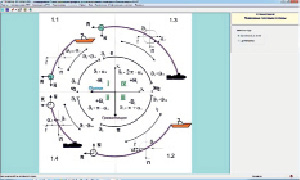
Рис. 2. Кабельный круг для буксирных линий
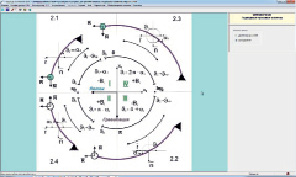
Рис. 3. Кабельный круг для буйрепов
С помощью подобной методики и используя представляемую программу, можно рассчитать статическую форму любой незамкнутой подводной тросовой системы со структурой «дерева», компонуя конфигурацию из отдельных составляющих её участков, «гибкая связь + твердое тело», для чего применяется встроенный конструктор конфигураций.
Программа адаптирована для использования её на стадии проектирования подводно-технических средств, а также для оперативного планирования подводно-технических работ в процессе их выполнения. Достоверность получаемых расчетов неоднократно проверена в ходе проведения морских испытаний.
О создании компьютерных моделей подводных робототехнических систем
Компьютерное моделирование является эффективным средством исследования физических явлений, происходящих в процессе функционирования подводных роботов и робототехнических систем. Под компьютерным моделированием понимается имитирование реально протекающих процессов в степени, достаточной для изучения поведения исследуемого объекта.
Целью компьютерного моделирования является составление рекомендаций для разработки унифицированных подсистем и технологий создания подводных роботов и робототехнических систем, в частности интеллектуальных систем управления.
Для осуществления поставленной цели необходимо решить следующие задачи:
– создать компьютерную модель робототехнических систем, включающую в себя модель робота и модель внешней среды;
– с помощью компьютерного моделирования исследовать режимы функционирования унифицированных подсистем и робототехнических систем в целом при выполнении ими типовых задач;
– составить рекомендации для разработки унифицированных подсистем и технологий создания подводных роботов и робототехнических систем, в частности интеллектной системы управления.
Компьютерная модель в рамках структурного моделирования состоит, в общем виде, из математической модели (математического описания натурного процесса) и моделирующих устройств, т.е. технических средств представления натуры. При использовании этой формы в модели создается структура дифференциальных уравнений динамики системы. Структура дифференциальных уравнений отображает физическую структуру динамической системы, передаточные функции её звеньев, нелинейные связи так, что уже в процессе подготовки модели проявляются основные свойства исследуемого объекта. При практической же реализации компьютерная модель должна состоять из трех частей:
– математического обеспечения;
– программного обеспечения;
– технического обеспечения.
Математическое обеспечение компьютерной модели подводной робототехнической системы состоит из:
– математической модели робототехнической системы;
– математической модели внешней среды.
Программное обеспечение является практической реализацией математической модели, на имеющихся вычислительных мощностях. Программное обеспечение можно разделить на базовое, т.е. неизменяемую его часть, которая не зависит от конкретного состава вычислительных средств, и изменяемую, состав которой определяется при каждой реализации типом используемой вычислительной платформы, набором внешних устройств, компьютеров и другими факторами.
Техническое обеспечение представляет собой программно-аппаратную модель, состоящую из базового компьютера и связанных с ним дополнительных внешних устройств. Последние могут быть либо частью натуры, либо имитаторами отдельных подсистем исследуемого объекта. Программными средствами здесь являются операционная система компьютера, вспомогательные и сервисные программы [5–7].
Заключение
Проведен анализ подводных робототехнических систем и предложена технология подхода и построения компьютерных моделей подводных робототехнических систем различного назначения, основанная на опыте создания необитаемых подводных аппаратов разных типов и многолетних теоретических исследований в области подводной робототехники. Создание математической модели механической системы с гибкими (неголономными) связями представляется чрезвычайно сложной задачей. Даже при составлении уравнений движения и их решении, для простейшего случая (известная задача двух тел с гибкой связью) возникают существенные затруднения. Имеется возможность упростить задачу путем сведения неголономных связей к голономным, что позволит широко применить аппарат аналитической механики системы твердых тел. Следует добавить, что при этом связи в системе должны быть реономны.
Работа выполнена в рамках государственного задания ФАНО России (тема № 0149-2018-0010) при частичной поддержке РФФИ (проект № Рго_а 17-05-41041)и РНФ (проект 14-50-00095).