science-review.ru
Явление дифракции волн проявляется в перераспределении энергии излучения в различных точках пространства при взаимодействии волн с экранами, огибании волнами препятствий, проникновении волн в экранированные участки пространства, в область «геометрической тени» и широко используется в различных областях волноводной техники [1–3]. Дифракция волн на различных структурах, достаточно подробно рассмотренная и описанная в литературе [4–6], посвящается преимущественно исследованиям влияния конфигураций экранов на дифракционную картину, методам расчета, вопросам точности расчета. Одной из ключевых является модель дифракции на щели, для которой рассчитывается интенсивность распределения света в зависимости от угла дифракции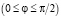 
и длины волны для плоских волн падающих перпендикулярно или под углом к плоскости щели [3].
Целью настоящей работы являлось теоретическое исследование зависимости поля дифракции от поперечной структуры поля падающего излучения. На основании анализа решений волновых уравнений получены аналитические соотношения для расчета дифракционной картины и проводится анализ влияния распределения поля падающего излучения в плоскости щели на дифракционную картину. Установлена зависимость интенсивности излучения от степени неоднородности излучения в плоскости щели в экране. Показано, что для неоднородности поля, описываемой квадратичной функцией, неоднородность структуры поля не влияет на положение дифракционных минимумов, а проявляется в изменении уровня дифракционных максимумов. Неоднородность, описываемая гармонической функцией, при высокой неоднородности приводит к сильному искажению дифракционной картины, формированию максимумов высокого порядка с интенсивностью большей, чем у максимумов нулевого порядка.
Рассмотрим дифракцию Фраунгофера на щели в плоском тонком экране (рис. 1). Разобьем открытую часть волновой поверхности (y = 0, 0 < x < a) на параллельные краям щели элементарные зоны излучения ширины. Волны, посылаемые вторичными источниками зонами в направлении угла φ, соберутся в точке экрана Р (рис. 1). Каждый вторичный источник в области щели dx создаст в точке Р колебание dEφ. Его амплитуда пропорциональна ширине dx элементарной зоны. Используя принцип Гюйгенса, имеем результирующую амплитуду колебаний, создаваемых вторичными волнами по всей ширине щели a в экране, в виде
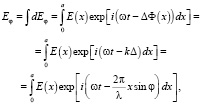
где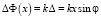 
– отставание по фазе колебаний, создаваемых зоной с координатой х от колебаний, создаваемых зоной с координатой х = 0, 
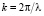– волновое число, λ – длина волны.
При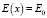 
, вводя параметр 
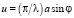, получаем для напряженности электрического поля известный результат, соответствующий работе [3]:
.
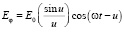Тогда интенсивность поля равна
.
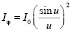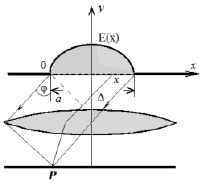
Рис. 1. Дифракция неоднородного по ширине щели поля
Рассмотрим влияние неоднородности по ширине щели поля падающего излучения на дифракционную картину. При этом рассмотрим интересные для практики случаи, когда интенсивность падающих волн максимальна в центре щели и спадает при приближении к краям щели.
Результаты исследования и их обсуждение
1. Рассмотрим случай, когда распределение напряженности поля описывается функцией
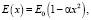
где α – параметр неоднородности поля. В этом случае может быть получено аналитическое решение для функции распределения поля дифракции в виде соотношения
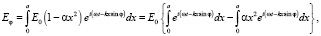
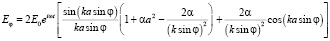
или, вводя для удобства анализа параметр u = ka sin φ, имеем
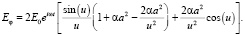
Коэффициент передачи волны через экран с отверстием в виде одиночной щели имеет следующий вид:
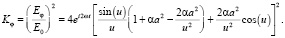
На рис. 2 показан график зависимости распределения интенсивности излучения в зависимости от параметра u, определяемого углом дифракции и нормированной на длину волны шириной щели в экране для различных коэффициентов α, характеризующих степень неоднородности поля в области щели. Из графика следует, что неоднородность поля падающей волны в области щели проявляется для данного типа неоднородности преимущественно в изменении максимумов интенсивности. Углы дифракционных минимумов от степени неоднородности поля не зависят.
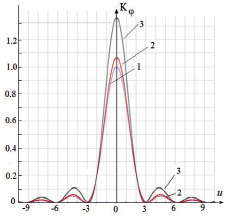
Рис. 2. Зависимость коэффициента передачи от параметра u = ka sin φ: 1 – αа2 = 0 – однородное поле, 2 – αа2 = 0,1, 3 – αа2 = 0,5
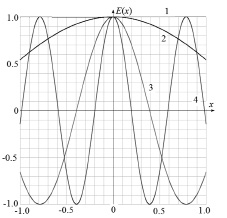
Рис. 3. Распределение поля в плоскости щели при различных параметрах неоднородности: 1 – d = 0 (однородное поле в области щели), 2 – d = 1 (малая неоднородность), 3 – d = 4, 4 – d = 8
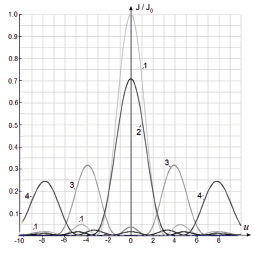
Рис. 4. Распределение интенсивности поля в области дифракции при различных соответствующих рис. 3 параметрах неоднородности поля в плоскости щели: кривая 1 – d = 0, 2 – d = 1, 3 – d = 4, 4 – d = 8
2. Для другого типа неоднородности поля, описываемой функцией
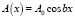
(b – параметр, характеризующий степень неоднородности поля),
поле дифракции принимает вид
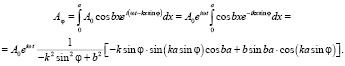
Или, вводя для удобства анализа обобщенный параметр d = ab, где a – ширина щели, имеем соотношение
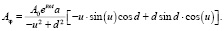
В частности, при b = 0 (равномерное в области щели распределение интенсивности падающей волны, распределение поля падающей волны в плоскости щели однородное, рис. 3, кривая 1) имеем известный [3] результат:
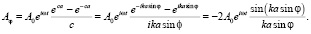
Распределение интенсивности поля дифракции для частного случая равномерного распределения поля по поперечному сечению падающего излучения (b = 0) представлено на рис. 4 (кривая 1).
На рис. 3 для сравнения показаны четыре случая распределения поля падающего излучения в области щели при различных параметрах неоднородности, характеризуемой обобщенным параметром d. На рис. 4 показано (соответствующее случаям распределения поля в области щели на рис. 3) распределение интенсивности поля в области дифракции в зависимости от параметра u = kasin φ, пропорционального углу дифракции.
На рис. 4 однородному в плоскости щели полю соответствует кривая 1. Различным параметрам неоднородного поля d > 0 соответствуют кривые 2, 3, 4. Анализ показывает, что при d < 2 (относительно малой неоднородности распределения поля) распределение интенсивности поля дифракции по параметру u, пропорциональному углу дифракции, качественно не меняется. При этом интенсивности в области максимумов уменьшаются, положение максимумов и минимумов первого и высших порядков сдвигается в сторону увеличения u (расстояние между максимумами высших порядков увеличивается). При увеличении неоднородности поля до уровня интенсивность максимума нулевого порядка падает до нуля, при этом, однако, формируются два новых максимума, интенсивность которых растет с ростом параметра d. Расстояние между максимумами растет с ростом параметра d. В диапазоне 2 < d < 2,5 центральный максимум переходит в локальный минимум, уровень интенсивности которого падает до нуля при росте неоднородности до d = 3.
Из графиков видно, что неравномерность поля в плоскости щели приводит к дополнительному перераспределению интенсивности: интенсивность максимумов растет и смещается в центр дифракционной картины. Это связано с изменением условия минимума по Френелю из-за неравномерности поля в области отверстия. Аналогичная картина наблюдается при других типах распределения интенсивности света в области отверстия. Таким образом, неравномерность поля в области отверстий в экранах может существенно влиять на дифракционную картину.
Заключение
Дифракция волн на экранах приводит к перераспределению энергии волн в пространстве, которое зависит от частоты (длины волны) и степени неоднородности поля в плоскости щели в экране и приводит [3] к частотному искажению сигналов, что необходимо учитывать при создании элементов систем связи. Поэтому ранее полученные результаты различных исследований, не учитывающие поперечной структуры падающего излучения, могут иметь существенную погрешность. Представляет интерес рассмотреть другие источники искажения дифракционной картины, в частности, движение сред, заполняющих структуры [7].