science-review.ru
В связи с интересом к решению переборных задач ([1, 2]), с одной стороны, возникает интерес к построению конкретных предметных областей (ПО), в которых такие задачи решаются просто (не более чем за полином от сложности декларативного описания ПО), а с другой – ПО, в которых число различных объектов много, и их перебор представляется трудоемким. В первом случае просто разрешимые ПО имеют сугубо прикладное значение, так как при их анализе удается экономить вычислительные ресурсы. Второй класс ПО со сложной разрешимостью имеет скорее теоретическое значение, демонстрируя, какие условия определяют их сложность.
Известно, что так называемые локальные ПО, определяемые, например, на логическом языке, просты для разрешения. Такие ПО характеризуются длинными описаниями своих объектов, и для них просто решаются задачи построения искомого объекта в силу ограничения вариантов поиска большим числом условий. Например, такие ПО описываются реляционными базами данных, в которых ответ на запрос (конечно, если он составлен рационально) не требует большого числа ресурсов. С другой стороны, существуют так называемые нелокальные ПО, которые обладают большим числом разнообразных объектов, и для них нахождение искомого объекта связано с большим перебором, который невозможно снизить без потери общности решения. Например, к таким задачам относятся задачи, формулируемые на графах, большое число комбинаторных задач и т.п. Исследование свойств локальности и нелокальности предметных областей приведено в [3], где эти свойства описаны на языке так называемых логических матриц.
Логические матрицы суть представления КНФ логических функции и определяются следующим образом. Пусть D = {D1, D2, ..., Dm} есть множество дизъюнктов, зависящих от переменных х1, х2, ..., хn. Множество D представляется матрицей MD, столбцы которой занумерованы от 1 до m, а строки – от 1 до n. Ее элемент aij = 1, если переменная хi входит в дизъюнкт Dj, aij = 0, если в Dj входит литера`хi, и aij есть символ подчеркивания «_», если ни переменная хi ни ее отрицание не входят в Dj. Символы 0 и 1 суть значащие, символ «_» – незначащий.
В работе представлены нелокальные логические матрицы, для которых число подфункций, получаемых различными означиваниями переменных, велико. Сопоставляя матрицам определенные графовые конструкции, удается построить графы, в которых велико число пустых подграфов. Тем самым, если граф полагать декларативным описанием ПО, то ее фактическое описание в виде перечисления пустых подграфов сложное.
Цель статьи состоит в описании так называемых нелокальных ПО, которые позволяют задавать декларативно просто описываемые ПО, обладающие большим числом принадлежащих им объектов.
Логические уравнения, матрицы и графы, определяемые уравнениями
Пусть S: Si = si, i = 1, 2, ..., m, m > 1, si∈{0, 1}, есть система булевских линейных уравнений от n переменных {x1, x2, ..., xn}, Si представляет собой сумму по модулю два в точности ki ≤ k различных положительных переменных из множества {x1, x2, ...,xn}, и каждая переменная входит в точности в два уравнения.
Верны следующие утверждения:
1. Система S уравнений имеет решение тогда и только тогда, когда выполняется равенство s1⊕s2⊕ … ⊕sm = 0.
2. В системе S уравнений каждая переменная существенная.
Поставим в соответствие системе S уравнений граф GS, содержащий m узлов, каждый его узел Ni помечен меткой si и ему соответствует уравнение Si = si, i = 1, 2, ..., m. Узлы Ni и Nj соединены ребром с меткой x∈{x1, x2, ..., xn}, если x есть общая переменная уравнений Si = si и Sj = sj. В графе GS метки всех ребер различные, и они покрывают все множество {x1, x2, ..., xn} переменных.
Понятно, что при различных распределениях меток узлов графа GS решения системы S различны.
Поставим в соответствие системе S уравнений логическую матрицу МS приведением каждой суммы Si в уравнении Si = 1 к КНФ и представлением каждого ее дизъюнкта в виде столбцов. Аналогично к КНФ приводится выражение ¬Si, если в S имеется уравнение Si = 0, i = 1, 2, ..., m. Если в уравнении Si = s, s∈{0, 1} имеются mi переменных, то в матрице Мi, соответствующей КНФ, содержится mi строк и 2mi – 1 столбцов. При s = 1 в каждом столбце матрицы Мi четное число нулей, а при s = 0 – нечетное. Матрицу Мi превращаем в матрицу, содержащую n строк (n – число различных переменных в уравнениях системы S), за счет добавления строк, соответствующих отсутствующим переменным, каждая такая строка имеет лишь незначащие символы «_». Матрица МS получается из всех таких матриц Мi, i = 1, 2, ..., m конкатенацией столбцов. Очевидно, что две матрицы Мi и Мj, имеют общую строку, содержащую значимые символы в столбцах, соответствующих обеим матрицам, тогда и только тогда, когда уравнения Si = si и Sj = sj имеют общую переменную, и эта строка соответствует этой переменной.
По матрице МS построим граф ортогональности GOrt, в котором число узлов совпадает с числом столбцов матрицы МS, каждому столбцу соответствует в точности один узел (потому считаем, что имена узлов совпадают с номерами столбцов) и каждому узлу приписан вектор, полученный транспонированием столбца. Два узла графа GOrt смежные тогда и только тогда, когда соответствующие столбцы матрицы, определяемые различными уравнениями, ортогональные. Тем самым при построении графа ортогональности не учитывается ортогональность узлов, определяемых любой, но одной матрицей Мi. Поэтому всякая матрица Мi в графе GOrt определяет пустой подграф Gi, узлы которого помечены ее столбцами.
Тогда каждая пара матриц Мi и Мj таких, что соответствующие уравнения Si = si и Sj = sj имеют общую переменную x, в графе GOrt определяет двудольный подграф (Gi, Gj) с долями Gi и Gj, который обладает следующим свойством: половина узлов подграфа Gi, смежных с узлами подграфа Gj, характеризуются нулевым значением переменной x, а половина – наоборот, единичным значением. Аналогично для подграфа Gj – половина узлов с нулевыми компонентами, соответствующими переменной x, а половина – с единичными. В результате в подграфе (Gi, Gj) выделяются два пустых подграфа, один из них характеризуется нулевым значением компонентов, соответствующих переменной x, а другой – единичным.
Отметим, что если в векторах, приписанных подграфам Gi и Gj, вычеркнуть компонент, соответствующий переменной x, то метки узлов каждого из этих подграфов образуют полное покрытие соответствующих единичных кубов. Размерности этих кубов на единицу меньше числа переменных в уравнениях, соответственно Si = si и Sj = sj.
Двойственными к выделенным пустым подграфам служат два полных двудольных подграфа, которые определяются следующим образом: в графе Gi все узлы первого двудольного графа характеризуются единичным компонентом приписанных векторов и нулевым в графе Gj. Для второго – наоборот, в графе Gi все его узлы характеризуются нулевым компонентом приписанных векторов и единичным в графе Gj.
Опишем преобразование матрицы MS и графов, когда переменная х, принадлежащая в точности двум уравнениям системы S, принимает значения sх = 0, 1. Пусть эта переменная входит в уравнения х⊕Si' = si, х⊕Sj' = sj, и х есть метка ребра NiNj. Если sх = 0, то уравнения превращаются в Si' = si и Sj' = sj, в графе GS ребро с меткой x стирается, и метки узлов Ni и Nj не меняются. Если sх = 1, то уравнения превращаются в Si' = 1 – si, Sj' = 1 – sj, в графе GS ребро x стирается, и метки узлов Ni и Nj инвертируются. Соответствующие преобразования матрицы МS следующие. Если sх = 0, то вычеркиваются все столбцы, имеющие на пересечении со строкой х нулевое значение, и затем сама строка х. Аналогично, при sх = 1, вычеркиваются все столбцы, имеющие на пересечении со строкой х единичное значение, затем вычеркивается строка х. Такие преобразования следуют из того, что матрица MS представляет логическую функцию в КНФ.
Рассмотрим, как подобное преобразование отражается на графе ортогональности GOrt. Если sх = 0, то в двудольном подграфе (Gi, Gj) выделяется пустой подграф Gx=0, который характеризуется нулевым значением компонентов, соответствующих переменной x. Если sх = 1, то пустой подграф Gx=1 характеризуется единичным значением компонентов, соответствующих переменной x. Теперь, если выбросить все ребра, определяемые переменной x, то получим два графа ортогональности GOrt(x=0) и GOrt(x=1), которые связаны с системами уравнений Sх=0, Sх=1, графами Gх=0 и Gх=1, матрицами Мх=0 и Мх=1 подобно исходным.
Производя сравнение матриц и графов, полученных в результате описанных преобразований, убеждаемся в верности утверждения: означивания sх = 0, 1 переменной x приводят к таким изменениям в системе S уравнений, графе GS, матрице МS и графе ортогональности GOrt, что результирующие системы уравнений, графы, логические матрицы и графы ортогональности связаны подобно исходным. Обозначим их соответственно Ssх, Gsх, Мsх и GOrtsх.
Аналогичными обозначениями будем пользоваться, когда рассматривается означивание sх совокупности х переменных. Пусть х есть совокупность переменных уравнений системы S, |х| = h, выделяющая подграф Gх, ребра которого помечены переменными из x. Узлы подграфа Gх образуют множество Nх, а ребра – множество Dх, |Dх| = h, каждое ребро из Dх помечено переменной из х, каждый узел из Nх инцидентен по меньшей мере одному ребру из Dх. Назовем узел N∈Nх внутренним, если ему инцидентны ребра только из множества Dх, в противном случае назовем узел N – граничным. Таким образом, каждый граничный узел смежный с некоторыми узлами вне Nх.
Полагаем, что число граничных узлов подграфа Gх равно k, N1, N2, ..., Nk суть все граничные узлы графа Gх, и Y1 ⊆х, Y2 ⊆х, ..., Yk⊆х суть подмножества переменных, которыми помечены ребра, инцидентные соответственно узлам N1, N2, ..., Nk. Так как метки ребер графа GS различные, то для несмежных граничных узлов эти множества различны. Пусть s есть означивание переменных х. Сформируем по s бинарный вектор s = (s1, s2, ..., sk), где si есть сумма по модулю двух компонентов из s, определяемых множеством Yi, i = 1, 2, ..., k. Назовем этот вектор ассоциированным с означиванием s.
Совокупность x переменных выделяет в графе ортогональности GOrt подграф GOrtx, ребра которого определяют отношение ортогональности, задаваемое переменными x. При означивании переменных x узлы именно графа GOrtx образуют интересующие нас пустые подграфы. В общем случае каждое означивание sx определяет пустой подграф GEmpsx, полученный вычеркиванием узлов и ребер подграфа GOrtx, как описано выше для одной переменной. В случае, когда рассматривается совокупность x переменных, преобразования осуществляются для каждой из них. В результате каждое такое означивание sx порождает и новый граф ортогональности. Однако различные означивания могут приводить к одинаковым как пустым подграфам, так и результирующим графам ортогональности. Поэтому оценим их число по логической матрице MS.
Верно следующее свойство ассоциированных векторов.
Лемма 1. Два означивания s1 и s2 переменных х определяют различные логические функции, соответствующие логические матрицы, графы и графы ортогональности, тогда и только тогда, когда s1 и s2 обладают различными ассоциированными векторами.
Доказательство. 1. Из определения ассоциированного вектора (s1, s2, ..., sk) следует, что если si = 1, то соответствующее означивание s переменных х приводит к инвертированию метки граничного узла Ni. Если же si = 0, то инвертирования нет. Отметим, что различные инвертирования приводят к различным логическим функциям. Таким образом, различные ассоциированные векторы соответствуют различным логическим функциям. Несовпадение логических матриц, графов и графов ортогональности вытекает из несовпадения логических функций.
2. Пусть означивания s1 и s2 переменных х определяют различные логические функции, но обладают одинаковыми ассоциированными векторами. Из определения ассоциативного вектора следует, что эти два означивания приводят к одному подграфу, в котором вычеркнуты все ребра с метками из множества х и все узлы, которым не инцидентно ни одно ребро. Следовательно, эти означивания определяют одну логическую функцию. Противоречие.
Лемма доказана.
Говорим, что означивания s1 и s2 переменных х эквивалентны, если они определяют одну логическую функцию.
Из способа формирования графов Gх и GOrtx получаем такое утверждение.
Следствие. Эквивалентные означивания s1 и s2 переменных х определяют одинаковые подграфы Gх и GOrtx.
Получаем, что признаком эквивалентности наборов, означивающих переменные х, является вид ассоциированного вектора. Поэтому представляет интерес количество различных классов эквивалентности в зависимости от числа компонентов ассоциированного вектора. Оценка снизу число различных классов эквивалентности означиваний переменных х приведена в [3]: все означивания переменных x разбиваются не менее чем на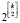 
различных классов эквивалентности.
Такое разбиение означиваний переменных x позволяет установить количество различных соответствующих матриц, подграфов и графов ортогональности. Верно такое утверждение: все означивания переменных х определяют не менее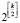 
различных логических функций, матриц, подграфов и графов ортогональности.
В данной статье нас интересует число различных пустых подграфов, которые можно выделить в исходном графе ортогональности. Исходим из того, что каждое означивание sx переменных x в графе ортогональности GOrt определяет пустой подграф, и неэквивалентные означивания определяют различные пустые подграфы. Из этого вытекает, что в исходном графе ортогональности GOrt имеется не менее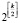 
различных пустых подграфов, число узлов в каждом из которых не менее |Gx|
Нелокальные области
Пусть степень вершин графа GS ограничена некоторой константой, и для него существуют константы 0 < c1, c2 < 1 такие, что любой подграф, обладающий c1n ребрами, имеет c2n граничных узлов. Такие графы называются расширителями [4]. Из указанного свойства расширителя и Следствия 1 вытекает
Теорема 2. Существуют матрицы с n строками, для которых мощность фактор-множеств означиваний части ее переменных не менее 2сn, где c – некоторая положительная константа.
Проблема нахождения пустых подграфов в произвольных графах имеет немалое прикладное значение [5]. В связи с этим интерес представляет такое утверждение.
Следствие. Существует граф ортогональности с n узлами, в котором имеется не менее 2сn пустых подграфов, где c – некоторая положительная константа.
Распределение пустых подграфов графа ортогональности
Каждому объекту построенной ПО можно поставить в соответствие частоту, с которой он определяется посредством означиваний переменных. Это позволяет определить энтропию ПО в зависимости от различных описаний объектов. Известно, что классы эквивалентности означиваний переменных x обладают одинаковыми долями независимо от порядка означивания переменных [3]. Каждому классу эквивалентности означиваний соответствует уникальный пустой подграф, выделяемый переменными x. Из последнего утверждения следует, что каждый такой пустой подграф определяется одинаковым числом означиваний переменных x. Следовательно, все объекты ПО обладают одинаковым распределением, а сама ПО – большой энтропией.
Заключение
В работе описано семейство логических матриц, для которых число классов эквивалентности, получаемых различными означиваниями переменных, ограничено снизу экспонентой от числа строк матрицы. Это позволяет построить графы, число пустых подграфов в которых ограничено снизу экспонентой от числа узлов. В результате описывается предметная область, для которой декларативное описание в виде графа – простое, но она содержит объекты, число которых не менее экспоненты от числа узлов. Тем самым построена декларативно просто описываемая ПО, в которой все объекты обладают одинаковыми совокупностями признаков, т.е. ПО, обладающая большой энтропией.