science-review.ru
За основу рассматриваемого подхода к построению бесплатформенной инерциальной навигационной системы (БИНС) приняты следующие четыре положения. Первое: в качестве инерциального датчика (ИЛ) БИНС использовано твёрдое тело в двух вариантах: А) установленное своими осями в два опорных узла и являющееся носителем нескольких вибраторов, обеспечивающих принудительные гармонические колебания подвижным элементам малой массы; Б) принудительно вращающееся вокруг оси, установленной на подвижном объекте в двух опорных узлах. Второе: указанное твёрдое тело имеет произвольные массогеометрические характеристики (МГХ) в связанной с ним системе координат (СК): массу, шесть компонентов тензора инерции и три координаты центра масс, которые идентифицированы с требуемой точностью. Третье: указанное твёрдое тело имеет два опорных узла, контактирующих с корпусом объекта и состоящих из нескольких работающих на сжатие датчиков сил, обеспечивающих измерение реакций опор этого твёрдого тела с требуемой точностью. Четвёртое: блок инерциальной информации (БИИ) включает в себя достаточное количество построенных указанным образом ИД, обеспечивающих получение не только полной, но и избыточной инерциальной информации.
Задача заключается в анализе принципиальной возможности построить схемное решение БИНС на основе принятых положений, то есть показать возможность выполнить математическое описание и составить алгоритм функционирования БИНС, включающий для каждого текущего момента времени измерение первичной информации и далее определение переменных: датчиковой информации, инерциальной информации, навигационной информации и определение функции управления движением объекта.
О математическом описании
Рассматривая ИД как механическую систему с учётом первого, второго и третьего принятых положений о ней и установленную на объекте, произвольно движущемся в инерциальном пространстве, применяя к указанной механической системе теорему об изменении главного вектора количеств движения и теорему об изменении главного момента количеств движения относительно начала связанной с объектом СК (называемого далее полюсом объекта), составляем шесть скалярных уравнений [1, 2]:
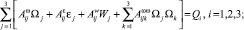(1)
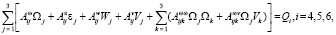
где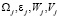 
– проекции на оси, связанной с объектом СК соответственно векторов абсолютной угловой скорости, абсолютного углового ускорения, кажущегося ускорения полюса объекта, скорости полюса объекта; 
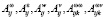– коэффициенты, зависящие от массогеометрических характеристик ИД и законов движения подвижных элементов вибраторов (для варианта А) во времени и законов движения вращающегося тела (для варианта Б). Правые части первой тройки уравнений (1) зависят от сил реакций опор твёрдого тела, правые части второй тройки этих уравнений зависят от моментов сил реакций опор твёрдого тела, а указанные силы реакций и моменты сил реакций опор зависят от параметров геометрии твёрдого тела и сил, действующих на подвижные элементы вибраторов с целью создания устойчивых вынужденных гармонических колебаний этих элементов [3] с заданными амплитудами и частотами (для варианта А) и моментов сил, приводящих во вращение твёрдое тело (для варианта Б). Можно показать, что указанные силы реакций и моменты сил реакций линейно зависят от сигналов датчиков сил, являющихся первичной информацией для БИНС. Перечислим параметры ИД и его установки на объекте, от которых зависят коэффициенты уравнений (1): углы ориентации СК, связанной с ИД (далее называемой датчиковой СК) относительно объектной СК; проекции радиусов-векторов начальных положений подвижных элементов вибраторов в датчиковой СК и их углов ориентаций в этой СК (для варианта А); массы подвижных элементов вибраторов (для варианта А); амплитуды, частоты и фазы гармонических колебаний вибраторов (для варианта А); закон изменения во времени момента, обеспечивающего вращение твёрдого тела (для варианта Б); МГХ твёрдого тела: масса, компоненты тензора инерции и координаты центра масс в датчиковой СК (для вариантов А и Б).
Согласно второму из принятых положений рассматриваемого подхода построения БИНС, МГХ твёрдого тела и остальные параметры ИД должны быть настолько точно идентифицированы или заданы, насколько этого требует точность переменных навигационной информации, точность которых зависит от точности переменных инерциальной информации, точность которых, в свою очередь, зависит от точности датчиковой информации: реакций опор твёрдого тела, точность определения которых зависит от точности первичной информации: сигналов датчиков сил. Другими словами, все указанные выше «точности» должны быть согласованными между собой для достижения конечной точности определения функции управления движением объекта.
Согласно четвёртому из принятых положений рассматриваемого подхода построения БИНС, в состав БИИ входят несколько ИД, математическое описание каждого из которых представлено шестью уравнениями (1), в каждое из которых в общем случае при произвольных величинах параметров ИД входит по тридцать переменных инерциальной информации вида [4]:
?i = xi, ?i = x3+I, Wi = x6+I, Vi = x9+I, i = 1, 2, 3;
?i?j = x12+3(i-1)+j, ?iVj = x21+3(i-1)+j, i, j = 1, 2, 3. (2)
Заметим, что переменные ?i, Wi i = 1, 2, 3 инерциальной информации из перечисленных в (2) являются основными, а остальные – избыточными, которые следует использовать для проверки правильности вычислений основных, например, путём проверки выполнения тождеств:
x12+3(i-1)+j = xixj, x21+3(i-1)+j = xix9+j, i,j = 1, 2, 3, (3)
то есть повышения надёжности определения указанных переменных, а значит, и повышения надёжности определения переменных навигационной информации и функции управления движением объекта. Следует отметить, что в общем случае ИД, входящие в состав БИИ, должны иметь неодинаковые параметры, перечисленные выше, для того, чтобы решения системы линейных алгебраических уравнений относительно переменных инерциальной информации:
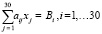(4)
существовали и были единственными, где aij – коэффициенты, зависящие от времени в силу наличия заданных законов движения во времени подвижных элементов вибраторов (для варианта А) и от конструктивных параметров всех ИД, входящих в состав БИИ, Bi – правые части, зависящие от величин реакций, определённых на основе измеряемых сигналов датчиков сил всех ИД. Решая систему линейных алгебраических уравнений (4) в бортовом компьютере, получаем величины переменных инерциальной информации (2), из которых переменные ?i, Wi, i = 1, 2, 3 являются основными и необходимыми для реализации алгоритма функционирования БИНС, а остальные переменные инерциальной информации из перечня (2) являются избыточными и должны быть использованы для проверки правильности определения основных переменных инерциальной информации, то есть должны быть использованы для повышения надёжности получаемой инерциальной информации, а следовательно, и повышения надёжности определения переменных навигационной информации и функции управления движением объекта.
В бортовом компьютере БИНС должен быть реализован алгоритм её функционирования на основе вычисленных переменных инерциальной информации ?i, Wi, i = 1, 2, 3, математическое описание для которого представляет собой систему пятнадцати обыкновенных дифференциальных уравнений [4–6]:
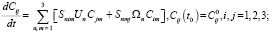
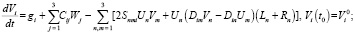
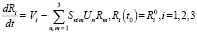(5)
и систему шести алгебраических уравнений, выражающих условия ортогональности и масштаба для направляющих косинусов от земной географической СК к объектной СК:
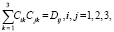(6)
где введены обозначения: Sijk – символ Леви-Чивита, Dij – символ Кронеккера, Ui, gi – проекции соответственно векторов угловой скорости Земли и гравитационного ускорения полюса объекта в земной географической СК; ?i, Wi – проекции соответственно векторов абсолютной угловой скорости объекта и кажущегося ускорения полюса объекта в объектной СК, являющиеся основными переменными инерциальной информации; Cij – направляющие косинусы от земной географической СК к объектной СК; Vi, Ri – проекции соответственно векторов скорости полюса объекта и радиуса-вектора полюса объекта (то есть координат объекта) в земной географической СК; C0ij, V0i, R0i – значения соответственно переменных Cij, Vi, Ri в начальный момент времени навигации объекта, то есть начальные условия движения объекта. Функция управления движением объекта может быть представлена в виде [7, 8]:
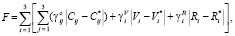(7)
где C*ij, V*i, R*i – программные функции времени переменных навигационной информации, соответствующие переменным Cij, Vi, Ri, вычисленным в бортовом компьютере БИНС;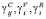 
– размерные весовые коэффициенты, определяемые зависимостями
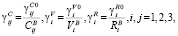(8)
где CBij,VBi, RBi – наибольшие значения переменных Cij, Vi, Ri на интервале времени [t0; T] навигации объекта;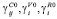 
– безразмерные весовые коэффициенты, которыми выделяется значимость того или иного слагаемого в формуле (7), удовлетворяющие условию
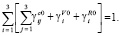(9)
Заметим, что функция (7) с учётом введённых весовых коэффициентов (8) представляет собой относительную величину рассогласования между заданными программными переменными навигационной информации и определяемыми БИНС переменными навигационной информации в каждый текущий момент времени из интервала [t0;T]. Далее, аналогично тому, как были введены единые обозначения ля тридцати переменных инерциальной информации зависимостями (2), целесообразно ввести единые обозначения для пятнадцати переменных навигационной информации:
Y3(i-1)+j = Cij, y9+i = Vi, y12-i = Ri. i, j = 1, 2, 3, (10)
тогда систему уравнений (5) можно записать в виде
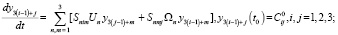
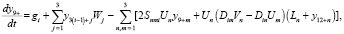
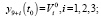
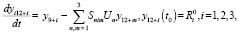(11)
а уравнения (6) можно записать в виде
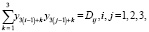(12)
и функцию управления (9) можно записать в виде
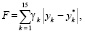(13)
где введены обозначения для размерных весовых коэффициентов:
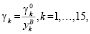(14)
а также введены обозначения: y*k – программные функции времени переменных навигационной информации, соответствующие переменным yk; yBk – наибольшие значения переменных yk на интервале времени [t0;T] навигации объекта, γ0k – безразмерные весовые коэффициенты, удовлетворяющие условию (11), которое в новых обозначениях переменных навигационной информации принимает вид
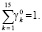(15)
Об алгоритме функционирования БИНС
Основу алгоритма функционирования БИНС представляет последовательность действий:
0) Задать в бортовом компьютере априорную информацию о параметрах всех ИД, входящих в состав БИИ, об угловой скорости Земли, её радиусе, её гравитационном поле, широте начала СК, связанной с Землёй, о начальных условиях движения объекта, о программных законах движения объекта, интервал времени, шаг решения по времени;
1) присвоить начальное значение времени;
2) измерить сигналы датчиков сил [9], то есть компоненты первичной информации;
3) вычислить коэффициенты уравнений (1) для всех ИД, входящих в БИИ;
4) вычислить реакции опор всех ИД (компоненты датчиковой информации);
5) вычислить коэффициенты левых и правых частей системы (4) для всех ИД, входящих в БИИ;
6) решить систему линейных алгебраических уравнений (4), то есть определить переменные инерциальной информации;
7) проверить выполнение тождеств (3) и если они не выполняются, то перейти к пункту 12, а если выполняются, то:
8) решить систему дифференциальных уравнений (11) относительно переменных навигационной информации на шаге по времени;
9) проверить выполнение условий (12) и если они не выполняются, то перейти к пункту 13, а если выполняются, то:
10) вычислить величину функции управления движением объекта (13) на шаге решения по времени;
11) замкнуть цикл по времени, увеличив текущий момент времени на шаг и проверив полученное значение времени с его конечным значением из заданного интервала с возвратом на пункт 2 или на пункт 14;
12) если тождества (3) не выполняются, то вывести сообщение об ошибке, обусловленной невыполнением тождеств (3) и перейти к пункту 14;
13) если условия (12) не выполняются, то вывести сообщение об ошибке, обусловленной невыполнением условий (12) и перейти к пункту 14;
14) закончить.
Об имитационной модели алгоритма функционирования БИНС
Правильность алгоритма функционирования БИНС зависит от достоверности информации сигналов датчиков сил и, соответственно, от правильного вычисления реакций опорных узлов ИД, входящих в состав блока БИИ. Проверка указанных достоверности и правильности должна быть реализована экспериментально после изготовления конструкций опорных узлов ИД. После проведения этих процедур и получения требуемых результатов остаётся вопрос о проверке достоверности алгоритма вычисления тридцати переменных xi, i = 1,…,30 инерциальной информации и пятнадцати переменных yk, k = 1,…,15 навигационной информации. Этот вопрос может быть решён теоретически на основе построенной имитационной модели функционирования БИНС, о которой далее идёт речь. Для построения указанной имитационной модели необходимо задать информацию о кинематических характеристиках объекта, для навигации которого предполагается использовать БИНС. Эти кинематические характеристики следует задать функциями времени: для поступательного движения объекта – проекциями радиуса-вектора полюса объекта в земной географической СК, их первых и вторых производных по времени; и для углового движения объекта – углами поворотов объекта относительно земной географической СК, их первых и вторых производных по времени на интервале [t0; T]. На основе этой информации путём математических преобразований методами кинематики произвольно движущегося в пространстве объекта, определяются переменные, являющиеся имитациями соответствующих переменных xi инерциальной информации, и далее определяются переменные, являющиеся имитациями соответствующих переменных yi навигационной информации. Далее, используя полученные функции времени – имитации для переменных инерциальной и уравнения (1), определяем имитации реакций опор ИД, после чего определяем имитации правых частей системы (4) и далее вместо системы (4) получаем соответствующую имитационную систему, решая которую получаем имитационные переменные инерциальной информации, которые сравниваем с найденными ранее соответствующими переменными из преобразований кинематических характеристик объекта. И наконец, используя имитации переменных инерциальной информации, путём решения системы обыкновенных дифференциальных уравнений (11) относительно переменных навигационной информации и сравнения полученных решений с соответствующими переменными, полученными из преобразований кинематических характеристик объекта, делаем вывод о правильности или неправильности алгоритма вычисления переменных навигационной информации. В случае правильности алгоритма на его основе следует разработать программу и инсталлировать эту программу в бортовой компьютер. В противном случае следует осуществить поиск и исправление ошибок.
Особенности и частные случаи
Уравнения (1) для ИД получены при произвольных величинах его параметров и при произвольной его установке на произвольно движущийся в пространстве объект. Если принять величины параметров инерциального датчика не произвольными, а удовлетворяющими некоторым ограничениям, достигаемым специальными конструктивными разработками, а также установить его не произвольным, а частным образом на объект, который совершает не произвольное, а некоторое частное движение, то из уравнений (1) можно «удалить» некоторые слагаемые и иметь не тридцать переменных инерциальной информации, как это имеет место в общем случае, а меньше. В этих частных случаях и построение блока инерциальной информации возможно на меньшем количестве инерциальных датчиков. Другими словами, можно специальными конструктивными разработками, реализованными в соответствии с критериями параметрического синтеза, обнулить коэффициенты при некоторых слагаемых в уравнениях (1) и превратить ИД общего вида в ИД специального вида, например, в датчик угловой скорости, датчик углового ускорения, датчик кажущегося ускорения. Но следует иметь в виду, что указанные конструктивные разработки необходимо реализовывать с точностью, согласованной с требуемой точностью определения функции управления движением объекта. Поэтому возникает альтернатива: точно идентифицировать реальные параметры ИД и пользоваться общими уравнениями (1) для получения в конечном итоге переменных навигационной информации или превратить ИД общего вида в ИД специального вида путём целенаправленных конструктивных разработок с использованием технологии реализации этих разработок необходимой точности. Построение инерциального навигационного комплекса описано в работе [10], а в работах [11, 12] приведены примеры построения конкретных БИНС для этого инерциального навигационного комплекса с использованием рассматриваемого подхода.
Выводы
1. Сформулирован подход построения БИНС, основанный на указанных во введении положениях.
2. Показаны принципиальные возможности выполнения математического описания для составления алгоритма функционирования БИНС и его имитационной модели.
3. Обозначены особенности в построении математических моделей БИНС в соответствии с рассматриваемым подходом и частные случаи.
Заключение
Построенные на основе рассматриваемого подхода БИНС имеют такие основные потенциальные преимущества перед традиционными БИНС, как однотипность инерциальных датчиков, изготавливаемых по единой технологии, наличие у этих датчиков избыточной инерциальной информации, позволяющей повышать надёжность и точность БИНС. Однако необходимо дальнейшее исследование, заключающееся в обоснованном предъявлении требований к точностным характеристикам инерциальных датчиков на основе заданной точности функции управления движением объекта. При получении положительных результатов в решении указанных задач БИНС, построенные на основе рассматриваемого подхода, могут быть применены для автономной навигации высокоскоростных маневренных объектов.