science-review.ru
Для большого числа прикладных задач, сводящихся к задачам на графах, интерес представляет исследование пустых подграфов [1, 2]. Особенно это важно при принятии решений в сложных предметных областях. Поэтому эффективная процедура построения всех нетривиальных пустых подграфов, удовлетворяющих определенным требованиям, представляется актуальной. Исходя из этого, в статье введена система преобразований графов и, в конечном итоге, – предложена процедура построения всех искомых пустых подграфов. Идея процедуры построения пустых подграфов выглядит так. Мы последовательно рассматриваем подграфы исходного графа, увеличивая их сложность и определяя для каждого пустые подграфы с искомыми свойствами. Процедура полна, поэтому по окончании работы выдаются все нетривиальные пустые подграфы.
Будем представлять пустые подграфы исходного графа, используя следующие признаки его узлов: узел входит в пустой подграф, узел не входит в пустой подграф и неизвестно, входит ли узел в пустой подграф. Причина возникновения последнего параметра такова. Решаемая здесь задача состоит в построении пустых подграфов, для которых выполняются определенные ограничения (например, на нижнюю оценку числа узлов). Построение осуществляется, переходя от подграфов меньшей сложности к подграфам с большей сложностью. В этом случае возможна ситуация, когда для некоторых подграфов непонятно, принадлежит ли конкретный узел его пустому подграфу, если факт принадлежности или непринадлежности можно установить лишь в последующем. Именно в этом случае используется термин неопределённость относительно вхождения конкретного узла.
Цель статьи: привести теоретический базис процедуры порождения полной совокупности максимальных пустых подграфов по заданному графу ортогональности.
1. Векторное представление графов. Построение максимальных пустых подграфов осуществляем относительно подграфов исходного графа ортогональности [3]. В частности, пусть G1 есть подграф графа G. Тогда пустой граф G'1⊆G1 называется максимальным в G1, если невозможно расширить множество его узлов за счет узлов только графа G1. Если G'1⊆G1 есть максимальный пустой подграф, то часть узлов G1 принадлежит G'1, а оставшиеся – не принадлежат. Принадлежность узлов подграфа G \ G1 расширению пустого подграфа G'1 характеризуется неопределенностью.
Пусть G'1 есть максимальный пустой подграф графа G1⊆G, N1 – есть множество узлов G'1, N0 – узлы подграфа G1 \ G'1. Обозначим N_ – множество узлов графа G, которые не входят в G1. Очевидно, что каждый узел из N0 смежный хотя бы с одним узлом из N1, и каждый узел из N1 смежный хотя бы с одним узлом из N0.
Пусть G1 и G2 суть подграфы графа G, и G1∪G2 есть их объединение, включающее ребра только этих подграфов. В исходном графе G могут встречаться ребра, инцидентные одновременно узлам G1 и G2, но в объединение G1∪G2 они не включены. Тем самым объединение G1∪G2 не расширяет множества ребер графов G1 и G2.
Пусть G'1⊆G1⊆G и G'2⊆G2⊆ G – максимальные пустые подграфы. Опишем максимальный в G1∪G2 пустой подграф, который есть подграф объединения G'1∪G'2. В него не включены узлы, которые не принадлежит хотя бы одному из подграфов G'1 или G'2. Таким образом, результирующему пустому подграфу принадлежат лишь часть узлов объединения G'1∪G'2, именно те, которые не принадлежат множеству G1\G'1∪G2\G'2. Тем не менее обозначим результирующий граф, полученный из пустых подграфов G'1 и G'2, как описано выше, также G'1∪G'2.
Распространим операцию ∪ на множества пустых подграфов. Пусть G*1 и G*2 суть множества максимальных пустых подграфов. Тогда G*1∪G*2 = {G1∪G2| G1∈G*1, G2∈G*2}.
Введем векторное обозначение подграфов. Пусть в графе G имеются N узлов, которые перенумерованы числами от 1 до N, и подграф G1⊆ G включает пустой подграф G'. Тогда подграф G' определяет вектор νG' = (ν1, ν2, …, νN) длины N, компоненты которого суть <0, 1, _>. Если узлы n1, n2, …, nq принадлежат G', то в векторе nG' на соответствующих местах n1, n2, …, nq стоит 1. Эти компоненты вектора nG' cуть единичные. Если узлы m1, m2, …, ms принадлежат дополнению G1 \ G', то в векторе nG' на соответствующих местах m1, m2, …, ms стоит 0. Эти компоненты вектора nG' суть нулевые. Иным узлам подграфа G \ G1 в векторе nG' соответствуют компоненты «_». Будем называть их не значащими, так как мы не знаем, будут ли входить эти узлы в расширение пустого подграфа G' по мере расширения графа G1.
Элементы базиса <0, 1, _> упорядочены следующим образом 0 < _, 1 < _. Компоненты 0 и 1 называются ортогональными. Это позволяет ввести лексикографический порядок на множестве векторов: векторы n1 и n2 находятся в отношении n1 < n2 тогда и только тогда, когда каждая пара (n',n") соответствующих компонентов векторов соответственно n1 и n2 находятся в отношении n' < n". В этом случае говорим, что вектор n2 поглощает вектор n1.
Введем произведение векторов над базисом <0, 1, _>: произведение ортогональных элементов равно 0, в остальных случаях ν1×ν2 = min(n1,n2). Затем распространим ее на векторы: произведение ν1×ν2 векторов n1 и n2 вычисляется покомпонентным умножением. Теперь распространим операцию×на множества векторов. Если n*1 и n*2 суть два множества векторов, то ν*1×ν*2 = {ν1×ν2| ν1∈ν*1, ν2 ∈ν*2}.
Пример 1. Пусть ν1 = (0, 1, _, 1, _), ν2 = (_, 1, 1, 0, _). Тогда ν1×ν2 = (0, 1, 1, 0, _).
Установим соответствие между операцией объединения пустых подграфов и произведением векторов. Пусть пустые подграфы G'1 и G'2 определяют векторы соответственно ν1 и ν2. Если узел n∈G'1, (компонент νn = 1), а в векторе, определяемом подграфом G'2, компонент νn ≠ 0, то узел n входит в объединение G'1∪G'2. И в векторе, определяемом G'1∪G'2, этому узлу соответствует единичный компонент. Аналогично, если узел n∈G'2 и в векторе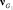 
компонент νn ≠ 0, то узел n входит в объединение G'1∪G'2, и в векторе, определяемом G'1∪G'2, этому узлу соответствует единичный компонент. Если же в векторе, определяемом подграфом G'1 или G'2, узлу n соответствует нулевой компонент, то узел n не входит в объединение G'1∪G'2, и в векторе, определяемом объединением G'1∪G'2, соответствующий компонент нулевой.
Таким образом, узел входит в объединение G'1∪G'2 подграфов, если он входит хотя бы в один подграф, а в другом отсутствует указание, что он в него не входит. Это обозначает, что единичный компонент, определяемый объединением, появляется лишь в случае, когда в одном векторе соответствующий компонент равен 1, а в другом он не нулевой.
Пример 2. Пусть подграф G'1 определяет вектор (1, 1, 0, _), а G'2 – (_, 0, _, 1). Тогда объединение G'1∪G'2 определяет вектор (1, 0, 0, 1).
Пример 3. Пусть полный подграф G с узлами 1, 2, 3, 4 является подграфом в графе с 5 узлами и не известно, какие ребра инцидентны узлу 5. Пустые подграфы подграфа G, определяют векторы: (1, 0, 0, 0, _), (0, 1, 0, 0, _), (0, 0, 1, 0, _), (0, 0, 0, 1, _). Здесь пятый компонент есть _, так как не известно отношение инцидентности узла 5. К этим векторам следует добавить вектор (0, 0, 0, 0, _), исходя из того, что узлы 1, 2, 3, 4 могут не входить в пустой подграф, когда в него входит узел 5. Учитывая наличие последнего вектора, можно ввести обобщение: теперь векторы образуют множество (_, 0, 0, 0, _), (0, _, 0, 0, _), (0, 0, _, 0, _), (0, 0, 0, _, _).
Пример 4. Пусть G есть веник с вершиной 1 и висячими узлами 2, 3, 4, имеется еще узел 5, для которого не известно отношение инцидентности. В этом случае пустые подграфы определяют векторы (1, 0, 0, 0, _), (0, _, _, _, _). Во втором векторе первые три не значащих компонента обозначают, что вхождение узлов 2, 3, 4 в пустой подграф определяется не известным отношением инцидентности узла 5.
Пример 5. Пусть два подграфа определяют векторы (0, _, _, 0) и (_, 0, _, _). Это значит, что в первый подграф не входят узлы 1 и 4, а во второй – узел 2. Про остальные узлы расширений этих подграфов ничего сказать нельзя. Тогда (0, _, _, 0)×(_, 0, _, _) = = (0, 0, _, 0). То есть в объединение соответствующих пустых графов не входят узлы 1, 2, 4. Про узел 3 ничего сказать нельзя.
Докажем теорему.
Теорема 1. Пусть подграфы G1, G2, …, Gq графа G, покрывают все его ребра. Каждый из них определяет множество максимальных пустых подграфов, соответственно G*1, G*2, …, G*q. Тогда G*1∪G*2∪ …∪G*q представляет собой множество пустых графов, которое включает все максимальные пустые подграфы графа G.
Доказательство проведем от противного. Допустим, имеется пустой подграф G', не принадлежащий объединению G*1∪G*2∪ …∪G*q и имеющий непустые вершинные пересечения G'1, G'2, …, G'm, соответственно с графами Gi1, Gi2, …, Gim совокупности G1, G2, …, Gq. Не уменьшая общности, можно считать, что G'1, G'2, …, G'm суть максимальные пустые подграфы соответственно в Gi1, Gi2, …, Gim. Но тогда G' = G'1∪G'2∪… ∪G'm принадлежит объединению G*1∪G*2∪ …∪G*q. Противоречие. Теорема доказана.
Таким образом, любая полная совокупность подграфов, покрывающая все ребра исходного графа, позволяет получить совокупность всех максимальных пустых подграфов. И для построения совокупности максимальных пустых графов, удовлетворяющих определенным условиям, необходимо выбирать наиболее рациональное покрытие графа подграфами G1, G2, …, Gq.
2. Вывод на графах. Используя операцию×на множестве векторов, определим понятие вывода, основываясь на бинарном правиле вывода: ν1×ν2⇒ν. Всякий вывод вектора ν из множества посылок {ν1, ν2, …, νq} можно представлять в виде однокорневого, растущего вверх бинарного дерева T, корню которого приписан вектор n. В T выше располагаются посылки, ниже заключения соответствующих правил, и листьям приписаны посылки {ν1, ν2, …, νq}.
Введем определение. Пусть ν есть вектор, определяемый некоторым подграфом. Результат ν* замены в нем всех единичных компонентов на несущественные компоненты назовем обобщением вектора ν. Очевидно отношение ν < ν*.
Следующий шаг состоит в том, что по выводу T вектора n строится, так называемое обобщенное дерево T* вектора n*, получающееся из T заменой всех векторов на их обобщения.
Справедливо утверждение.
Теорема 2. Обобщенное дерево T* является выводом вектора ν* из посылок, полученных обобщением всех посылок вывода T.
Доказательство. Рассмотрим правило вывода ν1×ν2⇒ν. Пусть ν*1 и ν*2 есть обобщения этих векторов. Покажем, что обобщение ν* вектора ν получается в результате применения правила ν*1×ν*2⇒ν*. Рассмотрим покомпонентные преобразования векторов, которые могут изменяться в результате применения операции ×. Операции, не содержащие 1, не меняются. Произведения 0×1 и 1×0 заменяются соответственно на 0×_ = 0 и _×0 = 0. Во всех случаях результат равен 0. Операция 1×1 заменяется на _×_, т.е. результатом является обобщение. Операции 1×_ = 1 и _×1 = 1 заменяются на _×_, что также является их обобщением. Таким образом, каждое правило вывода ν1×ν2⇒ν из T, превращается в правило вывода ν*1×ν*2⇒ν*. И, следовательно, вывод T превращается в вывод T* обобщения заключительного вектора вывода T. Теорема доказана.
3. Построение максимальных пустых подграфов. Введем такое определение. Два вектора n1 и n2 0-эквивалентны (обозначается n1 = 0n2), если совпадают их 0-компоненты.
Справедливы следующие утверждения:
Теорема 3. Пусть T есть вывод вектора n, и T* – обобщенный вывод вектора n*, полученный из T. Тогда выполняются отношения: n < n*и n = 0n*.
Теорема 4. Пусть имеется совокупность {n1, n2, …, nn} векторов таких, что их обобщения совпадают и равны n*. Тогда они принадлежат одному классу эквивалентности =0. Справедливо и обратное: если {n1, n2, …, nn} есть множество попарно =0–эквивалентных векторов, то их обобщения совпадают.
Переход к обобщающему вектору позволяет получить более экономные выводы. Справедливо утверждение 1.
Теорема 5. Пусть T* есть обобщенный вывод вектора n*, и n1 – его посылка. Тогда замена посылки n1 на вектор n2, такой что n1<n2 приводит к обобщённому выводу T1* вектора n1* такого, что выполняются отношения: n*<n1* и n* =0 n1*.
Таким образом, если в выводе вектора n* любой его вектор n и предшествующий ему вывод заменить на вывод поглощающего его вектора n', то заключением вывода будет вектор n'*, поглощающий первоначальный n*.
Пример 6. Рассмотрим граф K3, узлы которого перенумерованы 1, 2, 3. Ребро (1, 2) определяет следующие пустые графы: (0, 1, _), (1, 0, _), (0, 0, _); ребро (2, 3) – пустые графы: (_, 0, 1), (_, 1, 0), (0, 0, 0); ребро 1,3 – пустые графы: (0, _, 1), (1, _, 0), (0, _, 0). Если перейти к обобщающим векторам и отбросить поглощаемые, то получим векторы: {(0, _, _), (_, 0, _)}, {(_, 0, _), (_, _, 0),}, {(0, _, _), (_, _, 0)}. В результате из этого множества векторов выводятся следующие векторы: (_, 0, 0), (0, _, 0), (0, 0, _). Выводится еще вектор (0, 0, 0), но он поглощается каждым из первых трех.
Пример 7. Полный двудольный граф (1; 3) определяет в точности два попарно несравнимых вектора (_, 0, 0, 0) и (0, _, _. _).
Введем такие определения.
Пусть все пустые подграфы граф G определяют совокупность V попарно не сравнимых обобщенных векторов. Тогда V называется базисом графа G. Пусть G1, G2, …, Gm совокупность подграфов графа G и V1, V2, …, Vm суть базисы этих подграфов. Тогда максимальная совокупность всех обобщенных попарно не сравнимых векторов в множестве V1×V2×… ×Vm называется базисом совокупности G1, G2, …, Gm . Если G1, G2, …, Gm покрывает все ребра графа G, то он называется базисом графа G.
Пример 8. Для полного двудольного графа (n; m), базис состоит из двух векторов: в первом вначале расположены m нулевых компонентов, за которыми следуют n компонентов _, у второго наоборот – вначале m компонентов _, а затем n нулевых.
Справедлива теорема.
Теорема 6. Базис графа не зависит от выбора подграфов, покрывающих все его ребра.
Это утверждение представляет собой основу процедуры построения совокупности всех максимальных пустых подграфов по заданному графу, что имеет существенное значение при решении различных задач [4, 5]. Вкратце процедура получения пустых подграфов выглядит так. Пусть по заданному графу необходимо построить все его пустые подграфы, удовлетворяющие определенному условию. Таким условием может быть, например, нижняя граница числа узлов каждого пустого подграфа.
1. На вход поступает матрица смежности графа ортогональности. Каждая ее строка определяет веник, которому сопоставляется пара обобщенных векторов, описывающих его пустые подграфы.
2. В цикле, до получения неподвижной точки, строим попарные произведение этих векторов, попутно выбрасывая поглощаемые столбцы. При этом используется стратегия, минимизирующая число промежуточных подграфов, делая перебор управляемым содержательными особенностями предметной области.
3. На каждом шаге построения проверяются заданные условия, которым должны удовлетворять искомые пустые подграфы. Тем самым, поиск ведется только среди подграфов, которые удовлетворяют заданным условиям.
Заключение
Приведено теоретическое обоснование процедуры построения базиса графа, определяемого максимальными пустыми подграфами. Процедура реализована на языке C++ и работает на персональных компьютерах при решении практически значимых задач. Она использует различные стратегии поиска, что позволяет снизить перебор до приемлемого.