science-review.ru
Защищенность информации в современном цифровом мире целиком и полностью основывается на устойчивости современных криптосистем к различным информационным атакам. В то же время, учитывая стремительный рост в исследовании области квантовой криптографии, можно предположить, что появление квантовых компьютеров станет угрозой для современных криптосистем, защищенность которых зависит от сложности некоторых вычислительных задач, таких как факторизация больших простых чисел, дискретное логарифмирование, задачи на решетках и других.
Учитывая вышесказанное, поиск более защищенных постквантовых криптографических систем является актуальным, так как повысит устойчивость информационных систем к атакам с использованием квантовых компьютеров.
Данная работа посвящена анализу современных постквантовых алгоритмов, а также содержит выводы по перспективе их использования для конструирования криптосистем эпохи квантовых компьютеров и возможные варианты модификации данных алгоритмов для повышения криптостойкости или скорости выполнения. Далее в статье будут рассмотрены современные постквантовые криптографические системы, такие как криптосистема Мак-Элиса, криптосистема Ниддерайтера, криптосистемы с использованием квантового хэширования, криптосистемы на основе задач на решетках, криптосистемы с обучением на ошибках.
Криптосистема Мак-Элиса
McEliece – криптосистема с открытыми ключами, основанная на основе теории алгебраического кодирования и разработанная в 1978 г. Робертом Мак-Элисом. Это была первая схема, использующая рандомизацию в процессе шифрования. В целом работу данной криптосистемы можно разбить на три основных алгоритма:
- алгоритм случайной генерации ключа, дающий на выходе открытый и закрытый ключи;
- алгоритм случайного шифрования, дающий на выходе шифротекст;
- детерминированный алгоритм расшифровывания, дающий на выходе исходный открытый текст.
Рассмотрим каждый из алгоритмов более подробно. Алгоритм генерации ключей выполняется в несколько этапов:
- выбирается линейный (n, k)-код С, который исправляет t ошибок. Далее для этого кода генерируется оптимальная порождающая матрица G [1, с. 128];
- для более сложного восстановления исходного кода, на шифрующей стороне генерируется случайная невырожденная k×k матрица S;
- здесь же генерируется случайная n×n матрица перестановки P;
- происходит вычисление публичной порождающей матрицы Gpub:
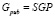(1.1)
- в виде открытого ключа представляется пара (Gpub, t), а в качестве закрытого – набор (S, G, P);
Блок-схему вышеописанного алгоритма можно увидеть на рис. 1.
Проанализируем более подробно каждый шаг алгоритма. На первом шаге необходимо сгенерировать так называемую оптимальную порождающую матрицу G. Оптимальной назовём матрицу, порождающую код С, который будет иметь максимальную корректирующую способность, то есть максимально возможное количество ошибок канала связи, которые код в состояннии исправить при декодировании [1, с. 128].
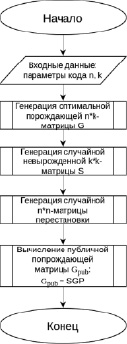
Рис. 1. Блок-схема алгоритма генерации ключей криптосистемы Мак-Элиса
Одним из возможных способов решения поставленной задачи является полный перебор всех возможных добавочных матриц вида Pk*(n-k). Для двоичного (n,k)-кода общее число таких матриц составляет 2(k*(n-k)), а сложность алгоритма приближается к экспоненциальной O(2n) [1, с. 129]. Данный метод является очень требовательным как к вычислительным, так и к временным ресурсам, с увеличением параметров кода будет существенно увеличиваться вычислительная сложность [1, с. 129].
О некоторых альтернативных способах поиска оптимальной порождающей матрицы можно узнать в следующих работах [1, 2].
Алгоритмы генерации матрицы S и матрицы перестановки P не требовательны к вычислительным ресурсам даже при существенном увеличении параметров кода.
Последний этап алгоритма с вычислением публичной порождающей матрицы Gpub представляет больший интерес с точки зрения анализа вычислительной сложности. Сложность вычисления произведения матриц по определению составляет O(n3) [3, с. 266], однако существуют более эффективные алгоритмы, которые применяются для перемножения больших матриц, такие как алгоритм Штрассена, алгоритм Пана, алгоритм Бини, алгоритм Копперсмита – Винограда и другие [3, с. 279].
Важно отметить, что в рамках данной работы все операции выполняются в GF(q) (поле Галуа).
Для выполнения алгоритма шифрования необходимо следовать следующей последовательности шагов:
- все сообщения m превращается в последовательность символов в поле GF(q) длины k;
- происходит генерация случайного вектора ошибки z, то есть вектора длины n и весом Хэмминга t;
- происходит вычисление шифротекста по формуле и дальнейшая его передача адресату:
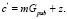(1.2)
Блок-схема алгоритма шифрования представлена на рис. 2.
И наконец, алгоритм расшифровывания включает в себя следующие этапы:
- вычисление обратной матрицы P-1;
- происходит первый этап декодирования, вычисляется кодовый вектор по формуле
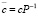(1.3)
- используется известный для рассматриваемого кода алгоритм декодирования, с целью получения 
из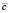 
;
- вычисляется исходное сообщение по следующей формуле
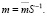(1.4)
Блок-схема алгоритма расшифровывания представлена на рис. 3.
С точки зрения анализа алгоритмов интерес представляет только операция поиска обратной матрицы, которая может потребовать чуть больше вычислительных ресурсов с увеличением длины кода. Сложность алгоритма поиска обратной матрицы по определению оценивается как O(n6) [4, c. 407]. Общая сложность будет выражаться некоторой степенной функцией, которая будет зависеть от выбора алгоритмов генерации оптимальной порождающей матрицы, матричного умножения и поиска обратной матрицы.
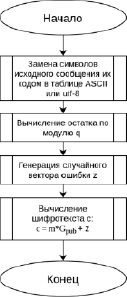
Рис. 2. Блок-схема алгоритма шифрования сообщения криптосистемы Мак-Элиса
После выполнения алгоритма расшифровывания работа криптосистемы Мак-Элиса завершается. Всё множество дешифрованных слов складывается в единый текст, который в точности совпадает с исходным.
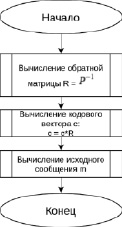
Рис. 3. Блок-схема алгоритма расшифрования сообщения криптосистемы Мак-Элиса
Алгоритм не получил широкого признания, но в то же время является кандидатом для постквантовой криптографии, так как устойчив к атаке при помощи алгоритма Шора. Алгоритм основан на сложности декодирования полных линейных кодов (общая задача декодирования является NP-сложной) и использует двоичные коды Гоппа, которые легко декодируются благодаря алгоритму Петерсона [5, c. 150]. Открытый ключ получается при помощи маскировки выбранного кода как полного линейного.
Существует несколько вариантов криптосистемы, использующих различные типы кодов. Большинство из них оказываются менее защищенными. Отдельного рассмотрения заслуживает вопрос выбора параметров криптосистемы.
До сих пор криптосистема Мак-Элиса с кодами Гоппы не поддается криптоанализу [6, c. 191]. Наиболее известные атаки используют алгоритм декодирования множества данныx. В других работах показано, что для квантовых вычислений размер ключа должен быть увеличен на четыре порядка из-за усовершенствования декодирования.
Криптосистема имеет несколько преимуществ, например над RSA. Шифрование и дешифрование проходит быстрее и с ростом длины ключа степень защиты данных возрастает. Долгое время считалось, что криптосистема Мак-Элиса не используется для ЭЦП должным образом. Однако оказалось возможным построить схему для ЭЦП на основе криптосистемы Нидеррайтера (модификация криптосистемы Мак-Элиса).
Прежде всего, рассмотрим криптостойкость рассматриваемой криптосистемы. В различной литературе можно найти множество всех возможных атак.
Большинство атак основаны на попытке построить декодер кода, генерируемого публичной матрицей Gpub. Такие атаки называют структурными. Если у кого-либо получится узнать Gpub, то закрытый ключ G будет довольно быстро раскрыт, что приведет к полному взлому криптосистемы. Злоумышленник в таком случае должен будет сравнить огромное множество эквивалентных кодов. При описании системы было предложено использовать в качестве достаточно криптостойкого (1024,524,50) – код. Таким образом, потребуется перебор более чем 2466 различных кодов.
Также имеют место атаки, анализирующие зашифрованный текст. На деле они оказались менее сложными по сравнению со структурными. Многие из них основаны на декодировании множества данных, что также называют парадоксом дней рождения.
Основные недостатки криптосистемы Мак-Элиса:
- размер открытого ключа слишком большой. При использовании кодов Гоппы с параметрами, предложенными Мак-Элисом, открытый ключ составляет 219 бит, что вызывает сложности в реализации;
- зашифрованное сообщение гораздо длиннее исходного;
- криптосистема не может быть использована для аутентификации, потому что схема шифрования не является взаимно-однозначной, а сам алгоритм является асимметричным.
Криптосистема Нидеррайтера
Криптосистема Нидеррайтера – криптосистема с открытыми ключами, основанная на теории алгебраического кодирования, разработанная в 1986 г. Харальдом Нидеррайтером [5, с. 432].
В отличие от криптосистемы Мак-Элиса криптосистема Нидеррайтера включает в себя следующее:
– использование проверочной матрицы кода;
– создание цифровой подписи;
– устойчивость к атакам с использованием алгоритма Шора;
Используемый в криптосистеме Нидеррайтера алгоритм основан на сложности декодирования полных линейных кодов, а также содержит следующее:
– генерацию ключей;
– шифрование исходного сообщения;
– расшифрование зашифрованного сообщения.
Рассмотрим каждый этап алгоритма по отдельности.
Генерация ключей происходит поэтапно:
- выбирается (n, k) – код C над полем Галуа GF(q), который способен исправить t ошибок. Выбранный код, конечно же, должен обладать эффективным алгоритмом декодирования;
- генерируется проверочная матрица H кода C, которая должна иметь размер (n – k)×n;
- случайным образом генерируется невырожденная (n – k)×(n – k) матрица S над полем GF(q) и матрица перестановки P размера n×n;
- вычисляется публичная проверочная матрица по формуле
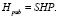(1.5)
Размерность представленной матрицы составляет (n – k)×n;
- в виде открытого ключа представляется пара (Hpub, t), а в качестве закрытого набор (S-1, H, P-1).
Блок-схема генерации ключей в криптосистеме Нидеррайтера представлена на рис. 4.
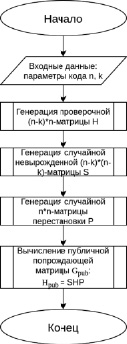
Рис. 4. Блок-схема алгоритма генерации ключей криптосистемы Нидеррайтера
Рассмотрим подробнее алгоритмы декодирования, которые можно применить на первом этапе.
Один из таких алгоритмов состоит в табулировании заранее вычисленных синдромов ошибок. Простейшим декодером такого типа является декодер Меггита, который проверяет синдромы только для тех конфигураций ошибок, которые расположены в старших позициях [7, с. 266]. Если вычисленный синдром находится в ранее сформированной таблице, то зашумлённый вектор исправляется в соответствии с подходящим вектором ошибок [7, с. 344]. Зачастую для реализации первого шага вышеописанного алгоритма применяются циклические коды, поэтому алгоритм декодирования будет реализован через полиномы.
Декодирование на основе решения алгебраических уравнений заключается в той простой идее, что каждой позиции кодового слова ставится в соответствие локатор ошибка. Декодирование состоит в отыскании локаторов, а в случае недвоичных кодов и значений ошибок – в символах, отмеченных локаторами [7, с. 397].
Мажоритарный алгоритм декодирования базируется на системе проверочных равенств. Система последовательно может быть разрешена относительно каждой из независимых переменных, причем в всилу избыточности это можно сделать не единственным способом [7, с. 401].
Алгоритм шифрования сообщения включает в себя выполнение следующих шагов:
- сообщение представляется в виде q-ичной подпоследовательности m длины n и имеющей вес t;
- вычисляется шифротекст по следующей формуле
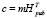. (1.6)
Таким образом, шифротекст в криптосистеме Нидеррайтера представляет собой синдром шифруемого вектора ошибки.
Блок-схема алгоритма шифрования в криптосистеме Нидеррайтера представлена на рис. 5.
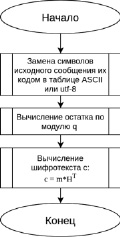
Рис. 5. Блок-схема алгоритма шифрования в криптосистеме Нидеррайтера
Алгоритм расшифровывания сообщения может быть описан следующим образом:
- нахождение синдрома s по следующей формуле:
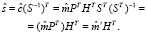(1.7)
Здесь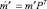 
, при этом вес 
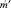не превосходит вес 
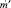, это означает, что, используя алгоритм декодирования, можно найти соответствующий текущему синдрому вектор ошибок;
- на этом шаге необходимо по синдрому найти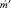 
и декодировать сообщение по следующей формуле:
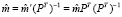. (1.8)
Блок-схема алгоритма шифрования в криптосистеме Нидеррайтера представлена на рис. 6.
Несмотря на то, что данная криптосистема была взломана, некоторые её модификации остаются криптостойкими [5, с. 501].
Преимущества криптосистемы Нидеррайтера:
- в отличие от криптосистемы Мак-Элиса, в криптосистеме Нидеррайтера не используются случайные параметры. Таким образом, результат шифрования одного и того же текста будет одинаковым. Этот факт позволяет использовать именно систему Нидеррайтера, а не Мак-Элиса, для создания электронно-цифровой подписи;
- размер открытого ключа в криптосистеме Нидеррайтера в порядки раз меньше, чем в криптосистеме Мак-Элиса [5, с. 530];
- по сравнению с RSA, скорость шифрования выше приблизительно в 50 раз, а дешифрования – в 100 раз [5, с. 534].
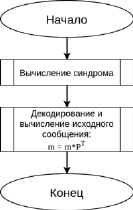
Рис. 6. Блок-схема алгоритма расшифровывания криптосистемы Нидеррайтера
Недостатки криптосистемы Нидеррайтера:
- размер ключей больше, чем в классических криптосистемах с открытым ключом, таких как RSA, Эль-Гамаль и других.
Квантовое хэширование
В отличие от алгоритмов классического хэширования, условно разработанных на однонаправленных функциях, квантовая криптография при построении хэш-функций основывается на принципах квантовой механики и квантовой теории информации, гарантирующих физическую однонаправленность квантовых хэш-функций. Эта особенность является одним из центральных потенциальных преимуществ перед классическими хэш-конструкциями. Для создания квантовых хэш-функций необходимо рассматривать универсальные хэш-семейства, которые являются основой цифровой подписи. Идея универсальных хэш-семейств заключается в обобщении понятия хэширования и хэш-семейств функций на квантовый случай, что означает отображение слов исходного сообщения в квантовые состояния, кубиты.
Кубит – единичный вектор в двумерном гильбертовом комплексном пространстве с таким свойством, что координаты вектора – комплексные числа, а сумма квадратов их амплитуд равняется единице. При таком определении кубит можно представить как вектор в трехмерном пространстве. Это означает, что кодирование сообщений можно проводить с помощью кубитов, для этого в теории квантовой информатики существует понятие квантового хэш-генератора – семейство функций, для каждой из которых можно построить отображения битов исходного сообщения в ансамбль из конкретного числа кубит, а также, скомбинировав их, получить квантовую хэш-функцию.
Сейчас можно говорить о том, что на создание действительно производительного квантового компьютера, который будет превосходить по вычислительной мощности все существующие классические машины, уйдет много времени. На данный момент остро стоит вопрос построения квантовой памяти, а именно, квантовых репитеров или увеличителей сигнала.
Обучение с ошибками
Обучение с ошибками – концепция машинного обучения, суть которой заключается в том, что в простые вычислительные задачи намеренно вносится ошибка, что превращает их решение известными методами в неосуществимую задачу за приемлемое время. Возникновение вышеописанной концепции отслеживается в работах Миклоша Айтаи и Синтии Дворк, которые первыми привели криптосистему на открытых ключах с использованием криптографии на решётках с последующими улучшениями и модификациями.
Диапазон криптографических приложений данной концепции достаточно широк. В качестве примера криптосистемы с использованием обучения с ошибками приведём криптосистему на открытых ключах. Система описывается следующими числами: n – секретный параметр, m – размерность, q – модуль и распределение вероятности случайной величины ε из поля Zn. Для гарантии безопасности и корректности системы следует выбрать следующие параметры для произвольной константы ε: q ≥ 2
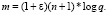(1.9)
Работа вышеописанной криптосистемы будет состоять из следующих алгоритмов:
- генерация ключей;
- шифрование сообщения;
- расшифровывание сообщения.
Данные алгоритмы удовлетворяют следующей последовательности шагов:
- секретный ключ описывается следующей формулой:
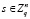(1.10)
- открытый ключ состоит из
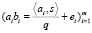(1.11)
- шифрование бита производится посредством выбора случайного подмножества S из [m] и определением шифра Enc(x) как
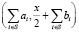(1.12)
- рисшифровывание происходит декодированием пары (a, b) в 0, если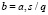 
ближе к 0, чем к 
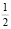, и 1 в противном случае.
Криптография на решётках
Решёткой называется множество
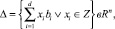(1.13)
где bi, i: = 1,…, d, линейно независимы над R.
Постквантовая криптография на решётках основана на неосуществимых как для квантовых, так и для классических компьютеров задачах на решётках, таких как:
- нахождение кратчайшего вектора;
- нахождение идеального кратчайшего вектора;
- нахождение кратчайшего независимого вектора;
- поиск короткого целого решения.
Данные задачи легли в основу некоторых криптографических конструкций, активно используемых на данный момент. К ним относят:
- GGH;
- NTRUSign.
Дадим подробное описание каждому из приведенных выше криптографических конструкций.
GGH – первая подпись, основанная на решетках, которая была представлена на CRYPTO в 1997 г. Голдрихтом и соавторами. Их идея заключалась в использовании решеток, для которых «плохой» базис, чьи вектора длинные и почти параллельные, является открытым, и «хороший» базис, с короткими и почти ортогональными векторами, является закрытым.
По их методу, сообщение необходимо хэшировать в пространство, натянутое на решетку, а подпись для данного хэша в этом пространстве является ближайшим узлом решетки. Схема не появилась с формальным доказательством безопасности, и ее базовый вариант был взломан в 1999 г. Nguyen. В 2006 г. модифицированная версия была снова сломана Nguyen и Regev [8, с. 157].
Опишем пошагово работу рассматриваемой криптографической конструкции:
- генерация ключей, которая состоит из открытого и закрытого ключей. В качестве открытого ключа выступает некоторый базис из решетки L вида
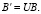(1.14)
Для некоторого М, пространство состоит из вектора (φ1,..., φn), где –М < φi < M. Закрытый ключ представляет собой базис B решетки L и унимодулярную матрицу U;
- алгоритм шифрования. Задается сообщение m = (φ1,..., φn), искажение е, открытый ключ 
. Процесс шифрования в векторной форме имеет следующий вид:
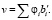(1.15)
Соответственно, в матричной форме имеет вид
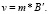(1.16)
Исходя из представленных выше формул, шифротекст имеет следующую структуру:
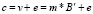(1.17)
- алгоритм расшифровки. Чтобы получить исходное сообщение, пользователю необходимо по формуле, представленной ниже, вычислить значение
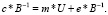(1.18)
Следовательно, исходя из соображений, часть e*B-1 убирается, тем самым формула (1.18) имеет следующую структуру:
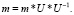(1.19)
NTRUSign – специальная версия GGH, отличающейся меньшим ключом и размером подписи и являющейся более эффективной. С другой стороны, она использует только решетки подмножества множества всех решеток, связанных с некоторыми полиномиальными кольцами. NTRUSign была выдвинута на рассмотрение IEEE-standard P1363.1 [8, с. 249]. Стойкость алгоритма обеспечивается трудностью поиска кратчайшего вектора решётки, которая более стойкая к атакам, реализуемым с помощью квантового компьютера.
Работа криптосистемы включает в себя следующие алгоритмы:
- генерация ключей;
- шифрование сообщения;
- расшифровывание сообщения.
Опишем генерацию ключей.
Для передачи сообщения от Алисы к Бобу необходимы открытый и закрытый ключи. Открытый знают как Боб, так и Алиса, закрытый ключ знает только Боб, который он использует для генерации открытого ключа. Для этого Боб выбирает два «маленьких» полинома f, g из R. «Малость» полиномов подразумевается в том смысле, что он маленький относительно произвольного полинома по модулю q. В произвольном полиноме коэффициенты должны быть примерно равномерно распределены по модулю q, а в малом – они много меньше q. Малость полиномов определяется с помощью чисел df и dg:
- полином f имеет df коэффициентов равных «1» и df-1 коэффициентов равных «–1», а остальные – «0»;
- полином g имеет dg коэффициентов равных «1» и столько же равных «-1», остальные – 0.
Причина, по которой полиномы выбираются именно таким образом, заключается в том, что f, возможно, является обратным, а g – нет (g (1) = 0, а нулевой элемент не имеет обратного).
Следующим шагом станет вычисление Бобом обратных полиномов fp и fq. Это можно пронаблюдать из представленных ниже формул:
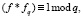(1.20)
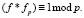(1.21)
Секретный ключ представляет собой пару (f, fp), а открытый h имеет следующий вид:
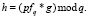(1.22)
Опишем процесс шифрования сообщения.
Сообщение представляется в виде полинома m с коэффициентами по модулю p. Далее выбирается полином r, определяемый с помощью числа dr следующим образом: количество коэффициентов равных «1» совпадает с теми, которые имеют значение «–1», оставшиеся – 0.
Используя эти полиномы, можно получить зашифрованное сообщение по формуле
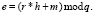(1.23)
Рассмотрим процесс расшифровывания поэтапно.
На первом шаге необходимо определить промежуточный полином вида:
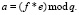(1.24)
Вторым шагом нужно расписать шифротекст, который со всеми возможными и необходимыми преобразованиями имеет вид
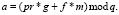(1.25)
На третьем шаге вычисляется значение полинома b, исходя из выбранных значений коэффициентов в диапазоне. Расчет производится по следующей формуле:
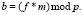(1.26)
На заключительном этапе, имея вторую половину секретного ключа и посчитанный полином b, Боб может расшифровать сообщение следующим образом:
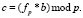(1.27)
На данный момент известны следующие атаки на вышеописанную криптосистему:
- полный перебор;
- встреча посередине;
- атака на основе множественной передачи сообщения;
- атака на основе решётки;
- атака на основе подобранного шифротекста.
Опишем параметры криптостойкости рассматриваемой криптосистемы.
Так как на сегодняшний день существуют быстрые алгоритмы поиска обратного полинома, в качестве секретного ключа стоит выбирать следующее значение:
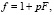(1.28)
где F – малый полином. В таком случае, выбранный ключ включает в себя следующее:
- f всегда имеет обратный элемент по модулю р;
- при расшифровке сообщения не нужно умножать на обратный полином fp.
Заключение
В качестве итога можно сказать, что на данный момент кандидатов-криптосистем для постквантовой криптографии предостаточно. Среди них криптосистемы, основанные на вычислительной сложности, которая будет предположительно достаточно высока и для производительности квантовых компьютеров, и криптосистемы, основанные на неосуществимости решения некоторых математических задач. Также стоит сказать и о том, что в области разработки постквантовых алгоритмов шифрования ведутся активные исследовательские работы, которые уже дают шокирующие результаты в плане повышения сложности криптосистем, к примеру, появление целой теории квантового хэширования. Все это даёт надежду на то, что область информационной безопасности окажется полностью подготовленной к появлению квантовых компьютеров и предоставит возможность обезопасить данные пользователей по всему миру.