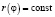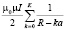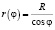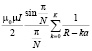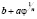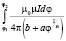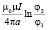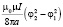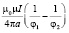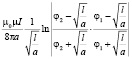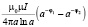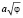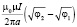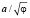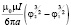science-review.ru
Уменьшение геометрических размеров элементов интегральных микросхем породило фундаментальную проблему создания планарных элементов, которые бы в малых размерах имела приемлемые значения электромагнитных параметров для построения сложных функциональных блоков, работающих в микро- и наноустройствах различных частотных диапазонов [1; 2].
Расчет элементов на базе уравнений электро- и магнитостатики часто приводит к неустранимым особенностям [3]. Этот недостаток теории потребовал создания новых физико-математических моделей [3; 4], которые были бы ориентированы на потребности планарной технологии.
Цель исследования: вывод аналитических соотношений для расчета магнитной индукции в центре наиболее распространенных планарных спиралей различной конфигурации используемых в микро- и наноэлектронике (рис. 1).
Материалы и методы исследования
Точный аналитический расчет магнитной индукции в планарных спиральных структурах высокой симметрии. Значение индукции магнитного поля В, которое создаётся ограниченными планарными спиралями в центре кольца, рассчитывается на основе закона Био-Савара-Лапласа [5] (рис. 2), где dB – элементарная магнитная индукция поля, создаваемая элементом тока Idl, μ0 = 4π?10-7 Гн/м – магнитная постоянная; dl – элементарный вектор длины, совпадающий по направлению с током (элемент проводника); I – сила тока; r – радиус-вектор, проведенный от элемента проводника к точке наблюдения, в которой определяется магнитная индукция (рис. 2).
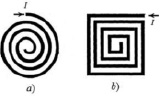
Рис. 1. Спиральные планарные структуры с плавным изменением радиуса витков
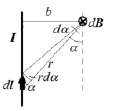
Рис. 2. Индукция магнитного поля dB, создаваемого элементом тока Idl
Результаты исследования и их обсуждение
Рассмотрим структуры двух типов.
1. Спирали из концентрических окружностей и многоугольников (рис. 3).
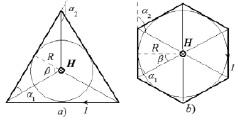
Рис. 3. Структура многоугольника с током (a – треугольник, b – шестиугольник)
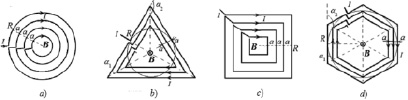
Рис. 4. Планарные спирали, сформированные круговыми витками (a) и многоугольниками (b, c, d)
Многие используемые на практике (рис. 1) конфигурации могут быть представлены как совокупность N кольцевых витков с током (рис. 4). Для расчета магнитной индукции в центре многоугольной структуры для одного витка с током, представленной на рис. 3, закон Био-Савара-Лапласа можно записать в скалярном виде [4; 5]:
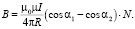(2)
Здесь R – радиус вписанной в многоугольник окружности, N – число сторон многоугольника, углы
, 
.
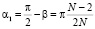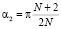Подстановка в (2) дает аналитическое соотношение:
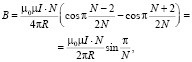
которое удобно представить в виде:
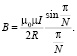(3)
Здесь первый сомножитель – это поле, создаваемое в центре кругового тока, а второй показывает разницу полей, создаваемых круговым током и многоугольником с числом сторон N. В случае прямоугольника со сторонами b, d (b ≠ d) магнитная индукция в центре определяется соотношением:
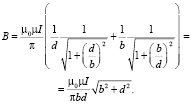
На рис. 4 (b, c, d) показаны планарные многовитковые структуры (с N = 3, 4, 6), сформированные подобными многоугольниками с меняющимися размерами сторон. В этом случае магнитная индукция для частного случая трехвитковой структуры (рис. 4, b) с числом витков k = 3 определяется соотношением:
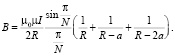
Для структуры из K – виткового многоугольника с числом сторон N (рис. 4, b, c, d)
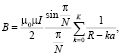
где a – расстояние между витками, причем (Ka < R).
Для K – виткового прямоугольника с внешними сторонами b, d и расстоянием между витками a
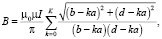
(Ka < b, d).
Для системы K – колец (рис. 4, а) магнитная индукция может быть рассчитана по формуле:
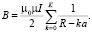
2. Расчёт магнитного поля в центре спирали с плавно меняющимся радиусом (рис. 1) будем проводить, используя закон Био-Савара-Лапласа в полярной системе координат:
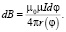
Общая формула для расчёта индукции в начале координат для любых спиралей [6; 7], описываемых функцией r(φ), представленной в полярных координатах, имеет вид:
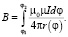
Для обобщённых спиралей вида [6; 7], описываемых функцией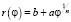 
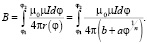
В частности, для одной из наиболее часто встречающихся спиралей – спирали Архимеда (n = 1, r(φ) = aφ) имеем:
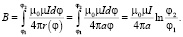
Предположим, что начальное положение спирали Архимеда находится в точке r = r1 и имеет угол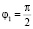 
, a ≠ 0. Это позволяет устранить особенность, возникающую в начале координат. Для гиперболической спирали (r(φ) = aφ) имеем:
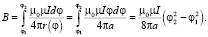
Для логарифмической спирали, описываемой функцией r = aφ, a > 0.
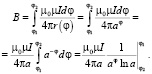
Для спирали Ферма,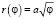 
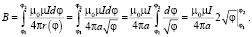
Спираль Литуус описывается функцией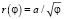 
, тогда
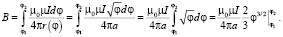
Спираль Галилея описывается функцией r = aφ2 – l, l > 0, тогда
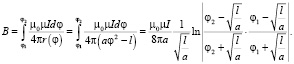
Если в спирали Галилея параметр l = 0, то мы имеем квадратичную спираль. Магнитная индукция в центре такой спирали описывается функцией:
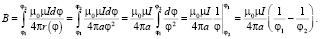
В таблице сведены формулы для расчета магнитной индукции в центре наиболее распространенных типов спиралей.
Магнитная индукция в центре различных спиралей
|
Вид спирали |
Уравнение спирали r(φ) |
Магнитная индукция B в центре спирали |
|
Система K – концентрических колец, радиусами R, R-a, …, R-ka |
|
|
|
Система K – концентрических правильных многоугольников |
|
|
|
Обобщённая спираль |
|
|
|
Спираль Архимеда |
aφ |
|
|
Гиперболическая спираль |
a/φ |
|
|
Квадратичная спираль |
a/φ2 |
|
|
Окончание таблицы |
||
|
Вид спирали |
Уравнение спирали r(φ) |
Магнитная индукция B в центре спирали |
|
Спираль Галилея |
aφ2 – l, l > 0 |
|
|
Логарифмическая спираль |
aφ, a > 0 |
|
|
Спираль Ферма |
|
|
|
Спираль Литуус |
|
|
Отметим, что используемым методом аналогичные соотношения могут быть получены для других типов плоских и объемных многовитковых спиралей на поверхности магнитодиэлектриков, в том числе с ферромагнитными или ферритовыми пленками с высокой магнитной проницаемостью μ >> 1 [8; 9].
Заключение
Получены аналитические решения задачи расчета индукции магнитного поля в центре спиралей наиболее распространенных конфигураций, на основе которых возможно создание планарных элементов микро- и наноустройств. Увеличение числа витков в спирали по сравнению с одиночным витком тока позволяет увеличить индукцию магнитного поля в центре спиралей, что позволяет создать на их основе индуктивности микро- и нанотехники. Дополнительное нанесение токопроводящих спиралей на поверхности магнитодиэлектриков с ферромагнитными или ферритовыми пленками с высокой магнитной проницаемостью позволяет существенно увеличить магнитную индукцию в центре спиралей и создавать на их основе плоские элементы с высокой индуктивностью.