Антропогенная деятельность – мощный фактор, влияющий на экологическое состояние агроландшафтов. Любая сельскохозяйственная деятельность заключается в получении гарантированно высоких урожаев сельскохозяйственных культур. Для получения таких результатов необходимо использовать все имеющиеся материально-технические, энергетические, трудовые, почвенные и природные ресурсы с наибольшей эффективностью. В Краснодарском крае из-за интенсификации производства земли сельскохозяйственного назначения постоянно нуждаются в восстановлении и сохранении плодородия. Усиление процессов деградации почв представляет реальную угрозу продовольственной, а значит и национальной безопасности страны [1; 2]. Деградация почв является прямым результатом деструктивной трансформации ландшафта, изменения направленности и интенсивности потоков веществ и энергии в процессе замещения природных фитоценозов агроценозами.
Цель исследования – разработка модели управления мелиоративными мероприятиями, не допускающими развития деградации почв. Внедрение высокоэффективных информационных технологий управления – одно из основных направлений развития наукоемких производств.
К ведущим показателям гидрогеологического мелиоративного состояния земель относится глубина грунтовых вод и их минерализация. Грунтовые воды являются чувствительными индикаторами на все антропогенные воздействия, осуществляемые на мелиорируемых территориях. Накопление солей в зоне аэрации можно регулировать величиной водоподачи и интенсивностью дренажного стока. Следовательно, уровень грунтовых вод можно рассматривать как функцию этих двух факторов, которые, в свою очередь, определяются затратами на строительство и эксплуатацию оросительной и коллекторно-дренажной сетей, наличием водных ресурсов [3].
Оценка оптимальности уровня грунтовых вод и управление им в пределах каждой системы на мелиорированных землях – одна из основных задач гидрогеолого-мелиоративной службы и эксплуатации, решение которой требует всесторонней информации о состоянии объекта.
Причина снижения почвенного плодородия, проявления деградационных явлений объясняется перегрузкой дренажно-сбросной сети, ухудшением окислительного режима почвы, вымыванием гумуса и питательных веществ из корнеобитаемого слоя почвы, подтоплением прилегающих площадей как занятых рисом, так и с суходольными культурами рисового севооборота [3].
Оценка оптимальности уровня грунтовых вод и управление им в пределах каждой системы на мелиорированных землях – одна из основных задач гидрогеолого-мелиоративной службы и эксплуатации, решение которой требует всесторонней информации о состоянии объекта. Рассмотрим один из наиболее распространенных критериев на региональном уровне – минимум суммарных приведенных затрат на сельскохозяйственное производство.
Найти min [CQQ + CxX + CyY], (1)
где X – площадь возделываемых культур (га), Y – площадь реконструкции (га),
Q – объем используемых водных ресурсов, тыс. м3,
CQ – удельные приведенные затраты на подачу воды, регулирование стока, руб./м3,
Cx – сельскохозяйственные издержки, руб./га,
Cy – удельные приведенные затраты на реконструкцию, руб./га.
Минимум суммарных потерь ищется при условиях:
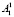 X +
X + 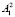 Y ≥ В1, (2)
Y ≥ В1, (2)
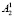 X +
X + 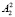 Y ≤ В2, (3)
Y ≤ В2, (3)
X, Y, Q ≥ 0. (4)
В неравенства (2), (3) матрицы 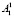 ,
, 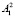 ,
, 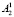 ,
, 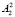 включают технико-экономические нормативы: агротехнологические коэффициенты, оросительные нормы, трудовые затраты.
включают технико-экономические нормативы: агротехнологические коэффициенты, оросительные нормы, трудовые затраты.
Наилучший вариант мелиоративного режима включает не только объем и качество урожая, но и затраты на стоимость ресурсов и ликвидацию отрицательных воздействий на окружающую среду.
1. Затраты на улучшение солевого режима (гипсование, промывки и т.п.), на поддержание определенного количества питательных веществ и гумуса.
2. Затраты на дренаж, на очистку дренажных вод, на защиту от подтопления соседних земель, штрафы за загрязнения вод (поверхностных и подземных).
3. Объем используемых ресурсов (сырьевых, энергетических).
4. Затраты на строительство и эксплуатацию мелиоративной системы с учетом конкретных (оптимальных) показателей мелиоративного режима.
Свойства почвы определяются набором показателей – физические, гидрохимические и другие характеристики. Оценки качества почв основываются на различных методах осреднения. Они полезны для сравнительной характеристики состояния почв, но по ряду критериев они неинформативны [4; 5]. Они не учитывают того, что на разных территориях и в различные периоды времени в системе контроля могут применяться неодинаковые перечни измеряемых приоритетных показателей свойств почв, а также различные методики измерений. Отсюда следует несопоставимость результатов осреднённых оценок. Кроме того, такие оценки не показывают, какая относительная часть территории должна рассматриваться как загрязнённая.
В развитии теории алгоритмов в области вычислительной техники предпочтительно использование векторного представления пространственных данных [6; 7]. Перечень параметров состояний и факторов, определяющих различие в проявлении экологических функций почв, должен совершенствоваться, а экологическое нормирование должно обеспечивать не только контроль состояния, но и предупреждения о наступлении самых первых признаков существенных изменений в почвах, ведущих к ее деградации. В расчетах необходимо учитывать затраты на компенсацию негативных воздействий на окружающую среду, а также стоимость ресурсов.
Основные принципы управления в мелиорации – системный подход; учет неопределенности целого ряда воздействующих факторов; бассейновый подход и опора на серьезные научные исследования и надежные данные; анализ современных водоресурсных систем [8]. Другой немаловажной предпосылкой применения системного подхода и математического моделирования служит резкое возрастание числа эколого-экономических параметров, которые необходимо учитывать при анализе и принятии решений по управлению.
Рассмотрим один из возможных вариантов процесса снижения цены намечаемого мероприятия [9–11].
Будем предполагать, что цена затрачиваемых мероприятий S(t) изменяется непрерывно со временем t, S(t) – монотонно убывающая функция с начальным значением 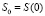 . Уравнение S(t) = S можно однозначно разрешить относительно аргумента t и получить соотношение t = t(S).
. Уравнение S(t) = S можно однозначно разрешить относительно аргумента t и получить соотношение t = t(S).
Считаем, что затрачиваемые мероприятия образуют пуассоновский поток постоянной интенсивности l. Выполненное мероприятие доводит систему до определенного состояния с вероятностью R(S), зависящей от цены S(t). Можно отметить, что R(S) – монотонно убывающая функция, так что с уменьшением цены мероприятий вероятность достижения ущерба возрастает. Существует некоторая минимальная цена Sm, так что R(Sm) = 1, то есть по этой цене отмечается наступление ущерба окружающей среде всегда. Рассмотрим вероятностные характеристики цены.
Цена Se, по которой состояние будет достигнуто, является случайной величиной.
За интервал времени 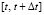 могут произойти следующие события:
могут произойти следующие события:
1) допустимое экологическое состояние системы не достигнуто. Вероятность этого события будет равна 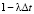 ;
;
2) допустимое экологическое состояние не достигнуто при проведенном мероприятии. Вероятность этого события равна 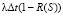 ;
;
3) мероприятие проведено, и допустимое экологическое состояние достигнуто. Вероятность этого события равна 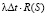 .
.
Подготовим выражение для математического ожидания цены состояния объекта:
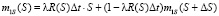 . (5)
. (5)
Разложим 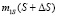 в ряд Тейлора:
в ряд Тейлора:
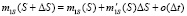 .
.
Подставив это разложение в (5), получим
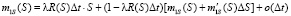 . (6)
. (6)
Выполнив преобразования, запишем:
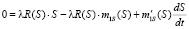 . (7)
. (7)
И введем функцию
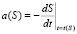 . (8)
. (8)
a(S) > 0, так как S(t) – убывающая функция. Запишем уравнение (8) в виде
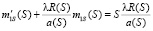 . (9)
. (9)
Выражение 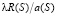 обозначим как g(S), то есть
обозначим как g(S), то есть 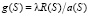 . Уравнение для
. Уравнение для 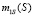 принимает вид
принимает вид
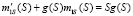 . (10)
. (10)
Запишем общее решение уравнения (10):
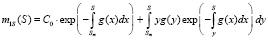 . (11)
. (11)
Константу С0 будем находить из условия: при минимальной цене Sm экологическое состояние объекта, удовлетворяющее требованиям, регистрируется с вероятностью 1, и поэтому должно быть 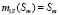 . Теперь получаем окончательный вид для математического ожидания цены состояния объекта [12]:
. Теперь получаем окончательный вид для математического ожидания цены состояния объекта [12]:
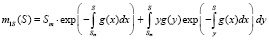 . (12)
. (12)
Подготовим выражение для дисперсии цены состояния объекта, то есть подготовим второй начальный момент рассматриваемой случайной величины 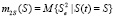 .
.
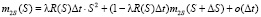 . (13)
. (13)
После преобразований, аналогичных используемым при выводе выражения математического ожидания, приходим к уравнению
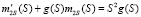 . (14)
. (14)
Решение уравнения (14) записываем в виде
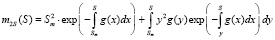 (15)
(15)
или
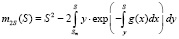 . (16)
. (16)
Знание 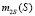 позволяет найти дисперсию цены состояния объекта
позволяет найти дисперсию цены состояния объекта 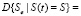
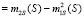 [13; 14].
[13; 14].
Рассмотрим распределение вероятностей цены состояния объекта. Найти плотность вероятностей цены можно, используя метод преобразования Лапласа. Найдем поэтому сначала преобразование Лапласа от плотности вероятностей цены, то есть функцию
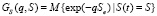 . (17)
. (17)
Рассуждения, аналогичные тем, которые производились при выводе уравнения для 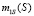 , приводят к соотношению
, приводят к соотношению
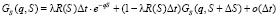 .
.
Разлагая 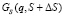 в ряд Тейлора, получим
в ряд Тейлора, получим
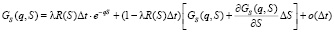 .
.
Раскрывая скобки, сокращая GS(q, S), деля на Δt и переходя к пределу Δt → 0, получим уравнение для GS(q, S):
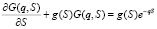 . (18)
. (18)
Решение этого уравнения имеет вид
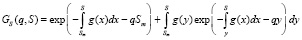 . (19)
. (19)
Обратное преобразование Лапласа от функции 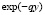 есть
есть 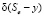 . Поэтому плотность вероятностей
. Поэтому плотность вероятностей 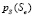 , являющаяся обратным преобразованием Лапласа от выражения (19), имеет вид
, являющаяся обратным преобразованием Лапласа от выражения (19), имеет вид
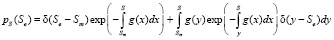 .
.
Используя свойства d-функции, получаем
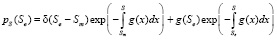 , (20)
, (20)
что и дает явный вид плотности вероятностей цены состояния объекта. При этом надо иметь в виду, что Se изменяется в пределах 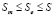 .
.
В дальнейшем намечаем рассмотреть ступенчатое изменение цены мероприятий, длительность времени наступления удовлетворительного мелиоративного состояния и оптимизационную задачу.
Заключение
Управление технологическим процессом сельскохозяйственного производства необходимо строить на принципах адаптивно-ландшафтного земледелия с учетом складывающейся экологической ситуации, не допуская возникновения необратимых негативных процессов. Исследования должны быть ориентированы не только на получение заданных объемов продукции, но и на сохранение и повышение плодородия почв, поддержание благоприятного состояние агроландшафта.
Эффективное управление оросительной системой невозможно без привлечения математического моделирования функционирования водохозяйственного комплекса. В статье предлагается математическая модель количественной оценки мелиоративных мероприятий с учетом неопределенностей оцениваемых параметров (систем, функционирующих в условиях неопределенности) и с учетом стохастического характера воздействия природно-климатических факторов. Использование разработанной вероятностной модели процесса управления намечаемыми мероприятиями позволит работникам агропромышленного комплекса снизить риски неопределенностей при принятии управленческих решений, учесть стохастический характер воздействия природно-климатических факторов.
Учет многофакторности природно-климатических, почвенных, водных показателей и критериев края является необходимой базой для разработки единой методологии по совершенствованию методов принятия решений с помощью математического аппарата, реализованного в математической модели и апробации результатов выполняемых исследований.
В рамках предложенной математической модели вычислены основные характеристики цены состояния объекта: ее математическое ожидание, дисперсия и плотность распределения вероятностей. Вероятностные модели процессов управления намечаемыми мероприятиями позволяют решить поставленные задачи и снизить риски неопределенностей при принятии управленческих решений.


 science-review.ru
science-review.ru