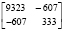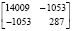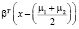Scientific journal

Scientific Review. Technical science

ISSN 2500-0799

ПИ №ФС77-57440

Методы уменьшения размерности важны во многих приложениях, связанных с машинным обучением, распознаванием образов [1], интеллектуальным анализом данных, биоинформатикой, биометрией и поиском информации. Основная цель методов уменьшения размерности состоит в уменьшении размеров путем удаления избыточных и зависимых объектов посредством преобразования объектов из пространства с более высокой размерностью в пространство с меньшими размерами. Существует два основных подхода по уменьшению размерности: неконтролируемый и контролируемый. При неконтролируемом подходе нет необходимости в маркировке классов данных, в то время как в контролируемом подходе методы уменьшения размерности учитывают метки классов. Существует множество методов сокращения неконтролируемой размерности, например независимый компонентный анализ (ICA) и неотрицательная матричная факторизация (NMF), но наиболее известным методом бесконтрольного подхода является анализ главных компонент (PCA) [2]. Этот тип уменьшения данных подходит для многих приложений, таких как визуализация и удаление шума [3]. Контролируемый подход также имеет много методов, таких как смешанный дискриминантный анализ (MDA) и нейронные сети (NN), но наиболее известным методом этого подхода является линейный дискриминантный анализ (LDA). Эта категория методов уменьшения размерности используется в биометрии, биоинформатике и химии. Метод LDA разработан для преобразования объектов в пространство более низкой размерности, которое максимизирует отношение дисперсии между классами к дисперсии внутри классов, тем самым гарантируя максимальную отделимость классов. Существует два типа метода LDA для работы с классами: зависящий от класса и независимый от класса. В классозависимом LDA для каждого класса вычисляется одно отдельное пространство нижних измерений для проецирования на него своих данных, тогда как в классонезависимом LDA каждый класс будет рассматриваться как отдельный класс по отношению к другим классам. В этом типе существует только одно пространство нижнего измерения для всех классов, чтобы проецировать на него свои данные. Хотя метод LDA считается наиболее широко используемым методом сокращения данных, он страдает от ряда проблем. Первой проблемой является то, что LDA не может найти пространство с меньшей размерностью, если размеры намного превышают число выборок в матрице данных. Таким образом, матрица внутри класса становится сингулярной, что известно как проблема малой выборки (SSS). Существуют различные подходы, которые предлагаются для решения этой задачи. Первый подход заключается в удалении нулевого пространства матрицы внутри класса, второй подход использует промежуточное подпространство (например, PCA) для преобразования матрицы внутри класса в матрицу полного ранга; таким образом, она может быть инвертирована. Третий подход, хорошо известное решение, заключается в использовании метода регуляризации для решения сингулярных линейных систем. Во второй задаче – задаче линейности, если различные классы нелинейно разделимы, LDA не может различать эти классы. Одним из решений этой проблемы является использование функций ядра [4].

Цель исследования: рассмотреть, что представляет собой LDA и как он работает, изучить алгоритм и методы вычисления пространства LDA, сравнить LDA с PCA.

Линейный дискриминантный анализ (LDA) – обобщение линейного дискриминанта Фишера – метода, используемого в статистике, распознавании образов и машинном обучении для поиска линейной комбинации признаков, которая характеризует или разделяет два или более классов объектов или событий. Этот метод проецирует набор данных на пространство с более низкой размерностью с хорошей разделимостью классов, чтобы избежать перенапряжения («проклятие размерности») и снизить вычислительные затраты. Полученная комбинация может быть использована в качестве линейного классификатора или чаще – для уменьшения размерности перед последующей классификацией [5].

Линейный дискриминантный анализ – контролируемый алгоритм, который учитывает меченые данные при использовании метода уменьшения размерности. Этот метод применяется для поиска нового пространства признаков, которое максимизирует разделимость классов путем использования подхода, очень похожего на тот, который применяется в анализе главных компонентов (PCA).

PCA – статистическая процедура, которая преобразует набор возможных коррелированных переменных в набор линейно некоррелированных признаков, называемых главными компонентами. Он существенно отбрасывает наименее важные переменные, сохраняя при этом ценные, находя главные компонентные оси, вдоль которых дисперсия данных высока [2].

В LDA мы намерены максимизировать разделение между классами путем максимизации расстояния между центроидами классов и в то же время минимизировать дисперсию внутри класса, чтобы образовались хорошо разделенные неперекрывающиеся кластеры. Минимизация внутриклассовой дисперсии приводит к созданию компактных, менее распространенных классов. Эти функции называются дискриминантными функциями.

Различные подходы к LDA

Наборы данных могут быть преобразованы, и тестовые векторы могут быть классифицированы в преобразованном пространстве двумя различными подходами [6].

Преобразование, зависящее от класса: этот тип подхода предполагает максимизацию отношения дисперсии между классами к дисперсии внутри классов. Основная цель состоит в том, чтобы максимизировать это соотношение так, чтобы была получена адекватная сепарабельность классов. Подход к классовому типу предполагает использование двух критериев оптимизации для независимого преобразования наборов данных.

Преобразование, не зависящее от класса: этот подход предполагает максимизацию отношения общей дисперсии к дисперсии внутри класса. Он использует только один критерий оптимизации для преобразования наборов данных, поэтому все точки данных независимо от их классовой принадлежности преобразуются с помощью этого преобразования. В этом типе LDA каждый класс рассматривается как отдельный класс по сравнению со всеми другими классами.

Алгоритм LDA

LDA основан на концепции поиска линейной комбинации переменных (предикторов), которая наилучшим образом разделяет два класса (цели). Чтобы захватить понятие отделимости, Фишер определил следующую функцию оценки [4].

,

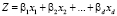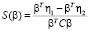– функция оценки,

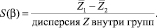
С учетом функции оценки задача состоит в том, чтобы определить линейные коэффициенты, максимизирующие оценку. Эта задача может быть решена с помощью следующих уравнений.

– коэффициенты модели;

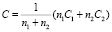– объединенная ковариационная матрица,

где β – коэффициент линейной модели;

C1, C2 – ковариационные матрицы;

μ1, μ 2 – средние векторы.

Одним из способов оценки эффективности дискриминации является расчет расстояния Махаланобиса между двумя группами [7]. Расстояние больше 3 свидетельствует, что в двух средних различаются более чем на 3 стандартных отклонения. Это означает, что перекрытие (вероятность неправильной классификации) довольно мало.

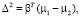
Δ – расстояние Махаланобиса между двумя группами.

Наконец, новая точка классифицируется с проецированием ее на максимально разделяющее направление и классификацией ее как C1, если:

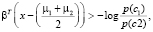
где βT – вектор коэффициентов;

х – векторные данные;

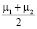– средний вектор;

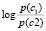– вероятность класса.

Пример:

Предположим, что мы получили набор данных от банка относительно его клиентов малого бизнеса, которые не выполнили свои обязательства (красный квадрат), и тех, кто не выполнил (синий круг), разделенных просроченными днями (DAYSDELQ) и количеством месяцев в бизнесе (BUSAGE). Мы используем LDA для поиска оптимальной линейной модели, которая наилучшим образом разделяет два класса (default и non-default) (рис. 1).

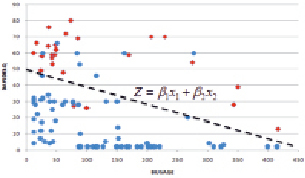
Рис. 1. График зависимости

Первым шагом является вычисление средних векторов, ковариационных матриц и вероятностей классов (табл. 1).

Затем мы вычисляем объединенную ковариационную матрицу и, наконец, коэффициенты линейной модели.

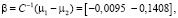
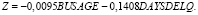
Расстояние Махаланобиса 2,32 показывает небольшое перекрытие между двумя группами, что означает хорошее разделение между классами по линейной модели.

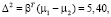
Δ = 2,32.

В следующей таблице мы рассчитываем Z-балл, используя приведенное выше уравнение Z. Однако оценка сама по себе не может быть применена для прогнозирования результата. Нам также нужно уравнение в столбце 5, чтобы выбрать класс N или Y. Мы прогнозируем класс N, если вычисленное значение больше –1,1, в противном случае класс Y. Как показано ниже, модель LDA сделала две ошибки (табл. 2).

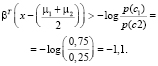
Сравнение LDA с PCA

Как линейный дискриминантный анализ (LDA), так и анализ главных компонент (PCA) являются методами линейного преобразования, которые обычно используются для уменьшения размерности (оба метода служат методами факторизации матрицы данных). Наиболее важным отличием между обоими методами является то, что PCA может быть описан как «неконтролируемый» алгоритм, поскольку он «игнорирует» метки классов и его цель – найти направления (так называемые главные компоненты), которые максимизируют дисперсию в наборе данных, в то время как LDA является «контролируемым» алгоритмом, который вычисляет направления («линейные дискриминанты»), представляющие оси, которые максимизируют разделение между несколькими классами [8].

Таблица 1

Средние векторы, ковариационные матрицы и вероятности классов

Таблица 2

Вычисление Z-оценки и прогнозирование

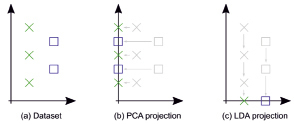
Рис. 2. Пример различного поведения подходов LDA и PCA для одного и того же набора данных. Набор данных представлен в (a). В (b) показан набор данных, спроецированный на основе того, что выбрал бы PCA, поскольку это максимизирует дисперсию независимо от меток классов (синие и зеленые цвета в этом случае). В (c) показан набор данных, спроецированный на основе того, что выбрал бы LDA, поскольку это максимизирует разделение классов, в данном случае зеленые и синие записи [9]

Они преследуют две совершенно разные цели (рис. 2):

– PCA ищет направления (компоненты), которые максимизируют дисперсию в наборе данных, поэтому ему не нужно рассматривать метки классов;

– LDA ищет направления (компоненты), которые максимизируют разделение классов, и для этого ему нужны метки классов.

Заключение

В статье были представлены и объяснены основные сведения о LDA. Авторы работы стремились дать общие сведения о том, что такое LDA, описать подходы к LDA, основной алгоритм LDA, а также было представлено небольшое сравнение алгоритмов LDA и PCA.