Подшипники скольжения нашли широкое применение в роторных машинах: в насосах, компрессорах, турбинах и многих других – благодаря своим уникальным достоинствам: возможности нести очень большие нагрузки, простоте конструкции, небольшим габаритам, долговечности (практически не зависящей от скорости вращения вала), способности гасить вибрации и некоторое время работать при перегрузках. Подшипники обеспечивают важнейшую для роторных машин задачу – фиксацию ротора в определённом положении, тем самым предотвращая задевание деталей ротора и статора; в частности, упорные подшипники фиксируют ротор в осевом направлении [1].
При высоких нагрузках и скоростях в современных роторных машинах практически безальтернативным вариантом является применение подшипников скольжения, работающих на режимах жидкостного трения, обеспечиваемого жидкими смазочными материалами [2]. В таких подшипниках должен обеспечиваться гидродинамический режим смазки, при котором на рабочих режимах между несущими поверхностями подшипника и вала образуется масляный слой с толщиной, достаточной для предотвращения перетечек масла через микронеровности поверхностей (для современных подшипников скольжения рекомендуется толщина слоя смазки больше 15 мкм). Ни в коем случае не допускается сильная вибрация подшипника, приводящая к его перегреву, снижению вязкости масла и к разрушению масляной плёнки [3].
Практика показала, что большинство аварийных остановок оборудования и его роторных агрегатов связано с выходом из строя именно подшипников скольжения. Причиной этого в большинстве случаев является неправильное проектирование подшипников, в связи с чем возникает перегрузка и перегрев, а как следствие – поломка узлов трения.
Таким образом, для обеспечения высокой надежности работы дорогого оборудования с подшипниками скольжения на всех режимах работы (пуск, рабочий режим, остановка), при их проектировании необходимо правильно учесть все действующие факторы. Эта задача является непростой, так как при работе подшипника протекает одновременно множество разнообразных физических процессов и явлений: трение, нестационарный перенос тепла маслом, теплообмен между маслом и колодками, изменение вязкости масла при изменении его температуры, фреттинг-износ [4] и др.
При исследовании и проектировании современных подшипников скольжения применяется гидродинамическая теория смазки, учитывающая вышеизложенные процессы [5].
На основе гидродинамической теории смазки, а также по результатам экспериментальных исследований и опыта эксплуатации были разработаны различные методики расчёта подшипников скольжения. В частности, для упорных подшипников скольжения, рассматриваемых в данной работе, широко применяется методика, изложенная, например, в [6].
Методика, предложенная в работе [6], основана на совместном использовании как точных формул (полученных из теории теплообмена, гидравлики и др.), так и эмпирических графиков и таблиц. В представленном виде расчёты по методике являются очень трудоёмкими и её невозможно использовать для вариантных расчётов подшипника при изменении режимов его работы (например, при изменении нагрузки или температуры масла на входе). Такой расчёт необходим не только для проверки режимов работы при эксплуатации существующих подшипников, но и для оптимизации конструкции и параметров при проектировании создаваемых роторных машин.
В представляемой работе поставлена цель создания удобной компьютерной программы, позволяющей производить автоматизированный расчёт основных конструктивных и режимных параметров упорных подшипников и выводить результаты в виде графиков.
Материалы и методы исследования
Конструкция гидродинамического упорного подшипника, рассматриваемого в данной работе, называемая «упорной пятой», описана, например, в работе [7] и изображена на рис. 1.
При вращении ротора 1 между плоской поверхностью упорного диска 2 и рабочими поверхностями колодок 5, разделённых межколодочными зазорами 4, образуется несущий слой смазочного материала вследствие того, что вращающийся диск увлекает масло в суживающийся зазор. Колодки закрепляются на упорной пяте 3 таким образом, чтобы при работе они могли поворачиваться и устанавливаться под углом по отношению к поверхности диска. Вытеканию масла из зазора препятствуют силы вязкости, которые преодолеваются возникающим давлением в клиновидном зазоре.
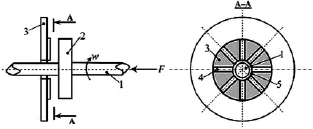
Рис. 1. Схема гидродинамического упорного подшипника: 1 – ротор; 2 – упорный диск; 3 – упорная пята; 4 – межколодочный зазор; 5 – упорная колодка
При расчёте представленной конструкции в качестве исходных данных используются: число оборотов ротора, осевое усилие, температура и давление масла на входе, диаметр шейки вала, наружный диаметр колодок, число колодок, коэффициент теплопроводности материала колодок.
Физические свойства масла (коэффициент теплоёмкости, удельный вес, коэффициент динамической вязкости) в методике определяются по таблицам после расчёта средней температуры масла в подшипнике.
Наиболее значимыми результатами расчёта упорного подшипника являются: оптимальные размеры колодок, средняя температура масла в подшипнике (на самых тяжёлых режимах работы не должна превышать 70 °С), минимальная толщина несущего слоя смазки (должна быть более 15 мкм), толщина упорного диска (исходя из максимально допускаемого его прогиба 1 мкм). Также вычисляются потери мощности на трение, необходимый расход масла через подшипник, площади входного и сливного дросселей.
Наиболее трудоёмким этапом перевода рассматриваемой методики в программный код являлась аппроксимация («оцифровка») представленных в методике графиков. Сложность заключалась в том, что в данном случае необходимо построение регрессионных функций двух переменным, так как коэффициенты k1-k6 зависят от двух параметров: отношения высоты колодки к её внутреннему радиусу b/r и центрального угла колодки θ.
Аппроксимация данных функций, а также физических свойств масел (вязкость, удельный вес и теплоёмкость в зависимости от средней температуры смазки в подшипнике) произведена в программе Approx – Simple Formula, основанной на применении метода наименьших квадратов [8] и подбирающей по введённым в неё точкам наилучшие регрессионные зависимости. Далее необходимо из предложенных зависимостей выбрать функцию с наименьшим среднеквадратичным отклонением точек от неё.
В качестве примера номограммы функции, для которой необходимо было найти аппроксимационную зависимость, на рис. 2 приведена функция k4.
Вначале выводятся функции одной переменной (полиномы) для каждого фиксированного значения второй переменной, имеющие одинаковый вид и отличающиеся только постоянными коэффициентами при слагаемых полинома. Затем каждый коэффициент полученных полиномов аппроксимируется по второй переменной и вместо постоянной становится функцией.
В результате аппроксимации рис. 2 выбрана следующая функция двух переменных – b/r и θ, дающая хорошее приближение к «оцифровываемой» функции k4:

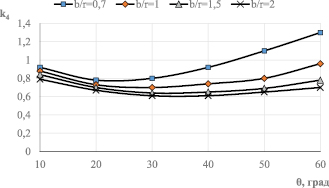
Рис. 2. Номограмма для определения коэффициента k4
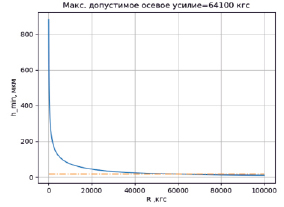
Рис. 3. Зависимость минимальной толщины несущего слоя смазки от осевого усилия
Далее в программе Microsoft Excel была произведена проверка качества аппроксимации – сравнивались графики функций k1-k6 из используемой методики расчёта подшипника с графиками, построенными по полученным регрессионным зависимостям. Сравнение подтвердило правильность «оцифрованных» функций.
Следующим этапом работы являлся пошаговый перевод методики [6] в программный код.
Для реализации возможности многовариантного расчёта подшипника был выбран высокоуровневый язык Python, который является, пожалуй, самым быстроразвивающимся средством разработки программ благодаря своей универсальности и практически безграничным возможностям. Он позволяет решать очень широкий круг задач – от математических и проектировочных расчётов до создания сайтов с удобным и современным интерфейсом. Его преимуществами перед другими языками являются удобочитаемость и высокая скорость разработки кода, лёгкость в обслуживании, повторном использовании и модификации программ [9]. Это возможно благодаря использованию специальных подключаемых библиотек, способных реализовывать различные функции. Например, для решения математических задач создана использованная в данной работе библиотека numpy.
Полученные вышеописанным способом регрессионные зависимости для коэффициентов k1-k6, а также для физических свойств масла (коэффициента теплоёмкости, удельного веса, коэффициента динамической вязкости), зависящих от средней температуры смазки, были использованы при разработке программного кода.
Результаты исследования и их обсуждение
С помощью созданной программы можно производить как поверочный расчёт уже применяемой конструкции упорного подшипника, так и проектировочный расчёт вновь создаваемой конструкции.
Результаты расчёта могут быть представлены как в числовом варианте, так и в виде графиков, иллюстрирующих зависимость параметров подшипника от исходных данных.
Для испытания программы осуществлён расчёт нескольких вариантов подшипников и произведено сравнение данных, полученных вручную и с помощью программы. Проверка подтвердила идентичность полученных результатов.
Далее был произведён проектировочный расчёт подшипника паровой турбины, прототипом которой является турбина Т-48/62-7,4/0,12 производства ОАО «Калужский турбинный завод». Исходные данные для расчёта упорного подшипника взяты по результатам теплового расчёта турбины. Максимальное осевое усилие на роторе 13025 кгс возникает в ней при работе на конденсационном режиме, с закрытыми отборами пара.
В качестве примера с использованием массивов модуля numpy [10] произведён расчёт зависимости устанавливающейся минимальной толщины несущего слоя смазки от прикладываемой к подшипнику нагрузки (осевого усилия). На рис. 3 приведён график данной зависимости, построенный с помощью модуля mathplotlib.pyplot для Python, основанного на модуле numpy [11].
По графику можно сделать вывод, что с увеличением осевой нагрузки минимальная толщина слоя смазки уменьшается. При максимальной проектной нагрузке 13025 кгс минимальная толщина несущего слоя смазки, равная 47 мкм, намного больше рекомендуемой, равной 15 мкм, следовательно, при данном режиме работы соприкосновения поверхностей сегментов и упорного диска не происходит.
Также запрограммировано выведение над графиком значения максимально допускаемого для подшипника осевого усилия, которое может возникнуть при эксплуатации турбины, например, в результате повреждения уплотнений. При превышении данного усилия гидродинамический режим смазки подшипника нарушается и, как правило, возникает авария. В приведённом примере при минимально допускаемом зазоре в подшипнике 15 мкм (на рис. 3 показан горизонтальной штрих-пунктирной линией) осевое усилие не должно превышать 64100 кгс.
Заключение
Таким образом, в рамках описанной работы по существующей методике расчёта упорных подшипников гидродинамической смазки разработана программа на языке Python, позволяющая решить следующие задачи:
- подбор оптимальных размеров упорных колодок и толщины упорного диска;
- расчёт средней температуры масла в подшипнике, которая не должна превышать допускаемую;
- расчёт минимальной толщины несущего слоя смазки, которая должна превышать 15 мкм;
- расчёт коэффициента трения и потери мощности на трение;
- расчёт необходимого расхода масла через подшипник и площадей входного и сливного дросселя;
- расчёт массивов требуемых исследователю результатов в заданном диапазоне изменения исходных данных и вывод всех необходимых зависимостей в числовом и наглядном графическом виде.
Разработанная программа может помочь проектировщику быстро осуществить разработку как новой оптимальной конструкции упорного подшипника, так и проверку режимов работы существующей конструкции при разных условиях эксплуатации. В конечном счёте автоматизация процесса проектирования приведёт к повышению надёжности подшипниковых узлов роторных машин. Примером проблемы, при решении которой может помочь данная программа, может являться уменьшение потерь мощности на трение при варьировании геометрических параметров подшипника, материала колодок и сорта масла [12] с обеспечением необходимой несущей способности.


 science-review.ru
science-review.ru