Отслеживание взгляда стало важной областью исследований с широким набором практических применений, включая взаимодействие человека с компьютером, медицинские исследования, вспомогательные системы для водителей и людей с ограниченными возможностями, маркетинговые исследования и биометрию [1]. Обнаружение границы и центра зрачка и вычисление положения его центра являются важными шагами во всех системах слежения за глазами и должны выполняться с высокой точностью.
Цель исследования: предложить эффективный и точный алгоритм поиска границ зрачка на изображении глаза, основанный на существующих методах компьютерного зрения.
Материалы и методы исследования
В большинстве исследований обнаружение зрачка осуществляется с помощью простых методов, которые недостаточно точны и дают сбой в случаях наличия искажений и помех на изображении. В этом исследовании мы сосредоточились на разработке эффективного алгоритма на основе признаков для обнаружения границ зрачка с использованием энтропии краевых сегментов.
Алгоритм представляет собой простой рабочий процесс и состоит из этапов, показанных на рис. 1. Обработка начинается с обнаружения области интереса (ROI) путем свертывания изображения глаза с помощью функции Хаара. Затем извлекаются краевые сегменты, каждый из которых представляет собой непрерывный массив пикселей. Следующим шагом является определение того, имеется ли почти круговой сегмент, который охватывает всю границу зрачка. Такой краевой сегмент будет существовать, только если зрачок хорошо виден без окклюзии или очень мал. Чтобы определить, имеет ли краевой сегмент круговую геометрию, используется быстрый эвристический метод, основанный на градиентном распределении краевого сегмента. При условии обнаружения почти круглого сегмента мы извлекаем эллиптические дуги только из этого сегмента. Если почти круговой сегмент не найден, что было бы в случае, если зрачок сильно закрыт веками или ресницами, то извлекаются дуги из всех краевых сегментов в области интереса.
После извлечения эллиптических дуг мы объединяем их в каждой возможной комбинации, чтобы сгенерировать набор кандидатов на эллипс, по крайней мере один из которых аппроксимирует границу зрачка. Наконец, кандидаты оцениваются на предмет их соответствия фактическому контуру зрачка, и наилучший, если он существует, выбирается среди эллипсов-кандидатов.
Результаты исследования и их обсуждение
На первом этапе алгоритма приблизительно оценивается площадь зрачка на всем изображении глаза. Зрачок можно описать как темный и компактный шарик, поскольку он состоит из более темных уровней интенсивности, чем окружающая его радужная оболочка, и обычно имеет эллиптическую форму с низким эксцентриситетом. Чтобы определить местонахождение области зрачка, используется квадратный Haar-подобный признак [2, 3], имеющий соотношение 3/5 между внутренней и внешней областями (рис. 2).
У человеческого глаза есть несколько физиологических свойств, которые различаются у индивидов: радиус глазного яблока, кривизна роговицы, расстояние между центром зрачка и центром роговицы и т.д. [4]. Размер зрачка также непостоянен как из-за физиологических различий между людьми, так и из-за расширения зрачка, которое происходит при изменениях освещенности. Поэтому применяется ядро Haar-подобного признака в нескольких масштабах и выбирается область, где дается максимальный отклик на единицу.
Для обнаружения всех краевых сегментов в области интереса используется детектор краевых сегментов Edge Drawing (ED) [5, 6]. Алгоритм ED работает, сначала идентифицируя набор точек на изображении, называемых якорями, а затем соединяя эти якоря таким образом, чтобы максимизировать градиентный отклик контуров пути, следовательно, обеспечивает хорошую локализацию края. ED выводит не только двоичную карту краев, аналогичную тем, которые выводятся обычными детекторами краев, но также показывает результат в виде набора краевых сегментов, каждый из которых представляет собой непрерывную и соединенную цепочку пикселей [7].
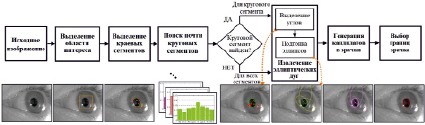
Рис. 1. Конвейер обработки предлагаемого алгоритма
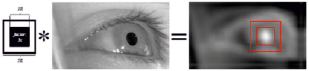
Рис. 2. Обнаружение области интереса с помощью операции свертки с квадратной функцией Хаара (слева) и результатом свертки (справа)
Как только краевые сегменты обнаружены, нужно найти тот, который представляет границу зрачка. Наиболее интуитивное решение состоит в том, чтобы подогнать эллипс к каждому краевому сегменту, вычислить ошибку подгонки и выбрать сегмент, имеющий наименьшую ошибку подгонки. Однако для подбора эллипса и вычисления ошибки подгонки для каждого сегмента требуется слишком много вычислений.
Чтобы уменьшить эту вычислительную нагрузку, используется более быстрый метод, основанный на анализе направлений градиента. Градиенты сегментов содержат существенную информацию о геометрической структуре и используются в задачах сопоставления, поиска и распознавания формы [8, 9]. Поскольку вертикальные и горизонтальные производные изображения глаза уже вычислены на этапе обнаружения краев, можно найти направления градиента с помощью значительно меньшего количества вычислений:
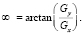
Функция arctan приводит значения углов в интервале [-90 °, 90 °], но, прежде чем исследовать распределение градиентов, следует произвести квантование углов с шагом 22,5 °, чтобы получить дискретные значения в восьми разных направлениях.
Получив квантованные направления градиента для всех пикселей в сегменте, можно определить характеристики формы этого сегмента. Нетрудно заметить, что круглые краевые сегменты будут иметь относительно равномерное распределение градиента, тогда как прямые сегменты имеют несбалансированное распределение, в котором доминируют несколько значений. Таким образом, можно выделить круглые краевые сегменты, используя функцию энтропии на квантованных градиентных распределениях сегментов:
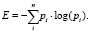
Поскольку функция энтропии максимизируется для плоских распределений, где частота каждого символа равна, энтропия распределения градиента для каждого отдельного краевого сегмента вычисляется следующим образом:
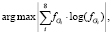
где fGi – частота i-го направления градиента. Значения энтропии градиентов краевых сегментов максимизируются для идеального круга и принимают нулевое значение для прямых линий, поскольку направление градиента вдоль прямой не меняется. Поскольку единичный круг квантуется в восьми направлениях, количество различных символов равно восьми, а максимальное значение энтропии равно log2 8 = 3. С помощью этой эвристики можно отказаться от порогового значения.
После вычисления градиентной энтропии краевых сегментов один сегмент выбирается в качестве сегмента, близкого к круглому, и из него извлекаются эллиптические дуги, если удовлетворяются следующие три критерия:
1) сегмент должен иметь высокую градиентную энтропию. Теоретическая верхняя граница энтропии для восьми различных направлений градиента равна log2 8 = 3. Соответственно, выбираются сегменты, которые имеют 2,8 или более градиентной энтропии;
2) сегмент должен иметь небольшую ошибку подгонки эллипса к образующим его пикселям, например 2 пикселя;
3) сегмент должен быть замкнутым. Чтобы избежать проблем из-за небольших окклюзий, таких как блики, используется порог в 15 пикселей для расстояния между начальной и конечной точками сегмента.
В случае если более одного краевого сегмента удовлетворяет всем трем условиям, указанным выше, в качестве почти круглого сегмента выбирается тот, который имеет минимальную ошибку подгонки эллипса. Хотя наличие почти круглого сегмента ускоряет вычисление, оно не является обязательным для обнаружения зрачка.
Следующим этапом алгоритма является извлечение эллиптических дуг из краевых сегментов, полученных на предыдущем этапе. Если на предыдущем этапе можно найти почти круговой сегмент, дуги извлекаются только из этого сегмента. Если почти круглого сегмента не обнаружено, то все сегменты, которые имеют высокую градиентную энтропию (то есть >2), подвергаются процессу извлечения дуги. Таким образом, алгоритм адаптируется и требует меньше вычислений, когда контур зрачка полностью виден. Ввиду того что прямая геометрия редко содержит эллиптические дуги, опускаются сегменты, имеющие низкую градиентную энтропию, а также короткие сегменты, чтобы сэкономить время вычислений.
Далее происходит обнаружение углов на сегментах с помощью метода быстрого масштабирования кривизны (CSS), который использует информацию о градиенте изображения для вычисления кривизны угла поворота [10]. Кривизна – это функция, которая указывает величину отклонения геометрической сущности (в данном случае контура ребра) от плоской. Вдоль контура края функция кривизны дает более высокие отклики при резких изменениях траектории. После этого к точкам, лежащим между двумя последовательными углами вдоль каждого сегмента, подгоняется эллипс, и получаются эллиптические дуги.
На рис. 3, Б–Г представлены результаты процесса извлечения дуги для нескольких тестовых изображений, которые показаны на рис. 3, А с извлеченным ROI. В первых двух рядах зрачок полностью виден; значит, обнаружен почти круговой сегмент (обозначен красным). Следовательно, извлечение дуги применяется только к этому сегменту. Когда из-за окклюзии не удается обнаружить почти круглый сегмент, дуги выделяют из всех сегментов, имеющих высокую градиентную энтропию, чтобы избежать пропуска какой-либо важной информации (рис. 3 – 3-й, 4-й и 5-й ряды).
На следующем этапе генерируются эллипсы-кандидаты путем группировки извлеченных дуг. Чтобы сформировать кандидатов в зрачки, мы пытаемся подогнать эллипс к каждому подмножеству всех извлеченных дуг. За исключением пустого множества, для n дуг имеется 2n-1 различных комбинаций дуг. На рис. 3, Д показаны все сгенерированные из извлеченных дуг кандидаты в зрачки.
Поскольку процесс генерации кандидатов в зрачки учитывает все подмножества выбранных дуг, группы несвязанных дуг, которые не образуют действительную эллиптическую структуру, также должны быть исключены после подбора эллипса.
Чтобы принять решение о выборе одного из кандидатов в качестве контура зрачка, используется функция стоимости Jc, которая учитывает следующие свойства эллипса-кандидата:
1) ошибка подгонки эллипса (ε);
2) эксцентриситет (е);
3) отношение пикселей дуги к периметру результирующего эллипса (φ).
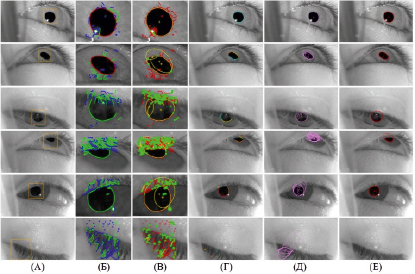
Рис. 3. Этапы обнаружения зрачка: (А) входное изображение с обнаруженной областью интереса; (Б) обнаруженные краевые сегменты в области интереса. Приблизительно круговой сегмент обозначается красным, если существует. Сегменты с высокой энтропией, которые подвергаются извлечению дуги, обозначены зеленым цветом. Короткие и имеющие низкую энтропию сегменты обозначены синим цветом; (В) обнаруженные углы (зеленые прямоугольники) и эллипсы, которые соответствуют пикселям, расположенным между двумя последовательными углами; (Г) извлеченные эллиптические дуги; (Д) множество кандидатов в границы зрачка; (Е) выбранный эллипс, представляющий контур зрачка
Каждый из зрачков-кандидатов образован одной или несколькими дугами. Если граница зрачка обнаруживается по нескольким дугам, ошибка подгонки должна быть разумной, потому что мы ожидаем, что дуги будут частями одного и того же эллиптического контура. Таким образом, нам нужно минимизировать ошибку подгонки ε.
Эксцентриситет (е) указывает на компактность эллипса или, другими словами, удаленность эллипса от круга, и вычисляется как
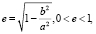
где a и b – большая и малая полуоси соответственно. Эксцентриситет равен 0 для круга и 1 для параболы. Среди кандидатов в зрачки, каждый из которых является подмножеством эллиптических дуг, существуют также разнообразные эллипсы, эксцентриситеты которых могут приближаться к 1. Однако проекция зрачка на плоскость изображения обычно ближе к кругу, чем к наклонному эллипсу.
Параметр φ представляет собой отношение числа пикселей, участвующих в подгонке эллипса, к периметру результирующего эллипса. В некоторых случаях одна короткая дуга может породить большой эллипс, что приводит к несогласованности. Поэтому выбираются кандидаты в зрачки, которые имеют большее значение φ.
Следует отметить, что влияние эксцентриситета (е) меньше, чем влияние ε и φ, поскольку существует возможность того, что истинный зрачок не будет самым компактным эллипсом среди кандидатов. Таким образом, среди кандидатов следует выбрать тот, который минимизирует следующую стоимостную функцию:
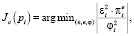
где pi – i-й кандидат, а π – постоянная.
Рис. 3, Е показывает результаты обнаружения зрачка для образцов изображений. Среди зрачков-кандидатов, показанных на рис. 3, Д, в качестве истинного зрачка выбран тот, который минимизирует Jc.
Заключение
Отслеживание глаз – это тема исследования, охватывающая широкий спектр вопросов, включая психологию, взаимодействие человека с компьютером, маркетинг, удобство использования и вспомогательные системы. Обнаружение зрачка является обязательным шагом во многих из этих приложений отслеживания глаз и должно быть выполнено быстро и точно. Точность алгоритма становится более очевидной в приложениях, таких как VR, AR, где пользователь контролирует или взаимодействует с другими объектами и интерфейсами.
Поскольку используемый метод обнаружения краевых сегментов обеспечивает оптимальную локализацию, извлекаемые эллиптические дуги точно окружают границу зрачка и аппроксимируют его центр. Кроме того, с помощью анализа распределения градиента повышается эффективность алгоритма за счет адаптивности и создается возможность для приложений реального времени, работающих с изображениями высокого разрешения.


 science-review.ru
science-review.ru