science-review.ru
Операторный метод построения решений дифференциальных уравнений был открыл Софусом Ли [1]. Им были предложены принципиально новые ряды – ряды, включающие в себя операторы:
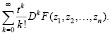
Здесь
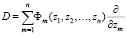
– заданный линейный дифференциальный оператор; степень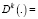 
, 
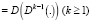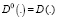, t, z1, z2, …, zn – комплексные переменные, Фm = (z1, z2, …, zn), F = (z1, z2, …, zn) – голоморфные функции комплексных переменных z1, z2, …, zn. В частном случае функции Фm = (z1, z2, …, zn) могут быть константами, и тогда дифференциальный оператор D будет с постоянными коэффициентами.
Нетрудно видеть, что ряд Ли может быть записан в символическом виде
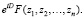
Замечание. Если функция F = (z1, z2, …, zn) – голоморфна в окрестности некоторой точки A = (z1, z2, …, zn), то для достаточно малых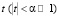 
будет иметь место соотношение (теорема В. Грёбнера):
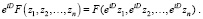
Кроме того, если в качестве оператора D взять
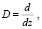
а за функцию F(z) – голоморфную функцию одной скалярной переменной z, то получим
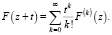
Откуда следует, что ряд Тейлора является частным случаем ряда Ли.
В 1970-х гг. ряды С. Ли изучались В. Грёбнером и его учениками. Были найдены также и многочисленные приложения этих рядов в теории уравнений, алгебраической геометрии, небесной механике, теоретической физике, в физике реакторов, в теории случайных величин. Операторное представление гармонических функций было построено А.В. Бицадзе, А.И. Лурье, Е. Майлсом, Е. Вильямсом, а явное представление их было дано А.Н. Филатовым и Б.А. Бондаренко [2]. А.Н. Филатову принадлежит также и развитие теории рядов Ли на решение линейных дифференциальных уравнений с частными производными, а также решение ряда прикладных задач теории упругости и вязкоупругости. Предложенные А.Н. Филатовым ряды Ли (их называют обобщенными рядами Ли) имеют вид
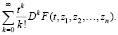
Здесь
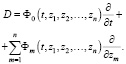
Отличие обобщенных рядов Ли от классических рядов Ли очевидно: переменная t, по которой ведется разложение в ряд, входит в функции Φm. Такое обобщение позволило распространить теорию операторных рядов на широкий класс линейных уравнений с частными производными. Некоторые результаты были также получены и для нелинейных уравнений. Позднее построенная А.Н. Филатовым теория обобщенных рядов Ли была развита на случай векторной переменной t = (t1, t2, …, tr), а также случай t = (t1, t2, …, tr, ...) и z = (z1, z2, …, zn, ...). Следующим шагом в применении операторного метода стало его распространение на интегро-дифференциальные уравнения. На этом пути были построены операторные ряды, включающие не дифференциальные операторы, а интегро-дифференциальные операторы. Кроме того, оказалось возможным развитие теории обобщенных рядов Ли и на вектор-операторы, как дифференциальные, так и интегро-дифференциальные [2, 3]. Заметим также, что квазиполиномиальные функции можно строить не только на дифференциальных или интегро-дифференциальных операторах, но и других типах операторов. Главное, чтобы для них можно было бы ввести классическое понятие степени.
В настоящей статье рассматривается интегро-дифференциальное уравнение, описывающее продольные линейные колебания вязкоупругого стержня в среде с сопротивлением. С помощью специальных функций, названных А.Н. Филатовым квазиполиномиальными, дается представление точного решения краевой задачи. При написании статьи мы опирались на работы [3–5], а также на классические работы по теории упругости [6–8].
Решение уравнения продольных колебаний прямолинейного вязкоупругого стержня
Рассмотрим тонкий, прямолинейный, однородный вязкоупругий стержень. Введем систему координат 0x, жестко связанную со стержнем. Стержень предполагаем находящимся в сопротивляющейся среде. Пусть момент времени, соответствующий началу переходного процесса (движению стержня), t0 = 0. Будем предполагать, что до начала движения скорости всех сечений стержня одинаковы [4]. Обозначим u(t, x) – перемещение сечения стержня с координатой x в момент времени t. Предположим, что связь между напряжением σx и деформацией εx в стержне задана следующим линейным законом:
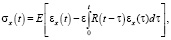
где E – модуль Юнга;
R(t – τ) – функция релаксации;
ε – малый параметр.
Рассмотрим случай линейной зависимости силы сопротивления от скорости движения. Тогда движение стержня в системе координат 0x будет описываться интегро-дифференциальным уравнением вида
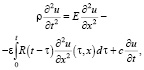(1)
где ρ – плотность стержня;
c – константа, отражающая сопротивление, пропорциональное первой степени скорости деформации стержня.
Замечание. Чтобы избежать дальнейших оговорок, будем считать, что уравнение (1) записано в безразмерных переменных.
Для уравнения (1) поставим краевое условие
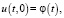(2)
где φ(t) – заданная функция времени t.
Зададим начальные условия
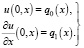(3)
Предположим, что функция φ(t) представима равномерно сходящимся рядом
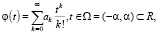(4)
где на коэффициенты ряда (4) наложены условия
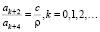(5)
Обозначим
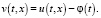(6)
Тогда заменой (6) приведем (1) к виду
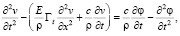(7)
где
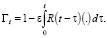
Так как, в силу свойства (5), правая часть уравнения (7) тождественно равна нулю, то (7) принимает более простой вид:
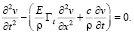(8)
Для уравнения (8) краевое и начальные условия перепишутся так:
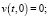(9)
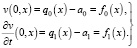(10)
Введем в рассмотрение следующие вектор-операторы [3]:
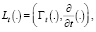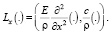(11)'
(11)"
Степени операторов Lt и Lx определим, как обычно, равенствами:
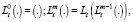
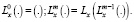
Уравнение (8), с учетом (11)’ и (11)», примет вид
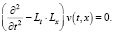(12)
Здесь Lt ? Lx обозначает скалярное произведение.
Представим теперь функции f0(x) и f1(x) в виде рядов Фурье по синусам
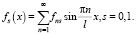(13)
А тогда, нетрудно убедиться, что в силу сделанных предположений квазиполиномиальная функция
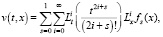(14)
будет решением задачи (12), (9), (10). Для доказательства, подставим (14) в уравнение (12). Тогда получим
.
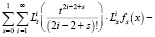
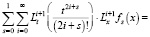
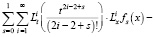
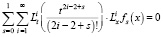Отсюда следует, что функция (14) есть решение уравнения (12). А так как, в силу (13), выполняется равенство
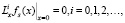
то функция (14) удовлетворяет и граничному условию (9). Кроме того, из (14) вытекает
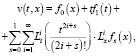
откуда
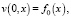
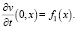
Следовательно, решение (14) удовлетворяет и начальным условиям (10). Таким образом, получено точное решение нашей задачи.
Для получения приближенного решения можно ограничиться конечным отрезком ряда (14). При этом встает задача аналитической или численной оценки полученного решения [9, 10]. Но это является предметом другого исследования.
Замечание. Изложенный выше операторный метод можно продемонстрировать и для дифференциального уравнения вынужденных колебаний стержня
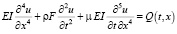. (15)
Здесь EI – жесткость стержня, F – площадь поперечного сечения, ρ – масса единицы объема, μ – коэффициент затухания, t – время, Q(t, x) – внешняя нагрузка.
Действительно, представим (15) в виде
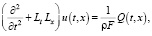(16)
где
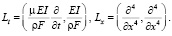
Далее предположим, что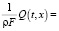 
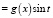, где функция g(x) имеет: 1) конечный полилинейный порядок q относительно оператора Lx; 2) 
.
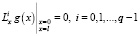Для уравнения (16) поставим начальные и граничные условия
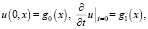(17)
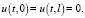(18)
Относительно функций g0(x) и g1(x) будем предполагать, что они обладают свойствами 1) и 2). Тогда, как нетрудно проверить, функция
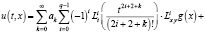
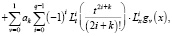
где ak – коэффициенты в разложении функции sin t в соответствующий ряд, будет решением задачи (16), (17), (18). В частности, если взять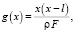 
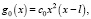
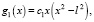c0, c1 – постоянные, то решением будет функция
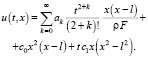
Заключение
Многие современные методы математической физики, например метод Трефца, Бубнова – Галеркина, коллокаций, наименьших квадратов, ортогональных проекций и другие, требуют в своем применении знания базисных координатных решений. Эти базисные системы функции конструируются как точные решения однородной задачи. В связи с этим определенный интерес представляют методы построения этих точных решений. Одним из эффективных методов построения точных решений уравнений с частными производными, а также интегро-дифференциальных уравнений является операторный метод, развитый А.Н. Филатовым, история развития которого связана с С. Ли и уходит истоками в конец XIX в. Выше мы применили метод А.Н. Филатова для задачи о продольных колебаниях вязкоупругого стержня. Полученное решение является точным, но при сделанном предположении о свойстве функции φ(t). Дальнейшее исследование аналитических свойств полученного решения можно провести с использованием каких-либо компьютерных математических пакетов с целью придания наглядности (визуализации) полученного решения и проведения качественного анализа в зависимости от параметров модели. Перспективным в этом направлении считаем использование систем символьных вычислений Maple, Mathematica, MatLab и др.