Достаточно часто, в теплоэнергетической отрасли и не только, встречаются случаи, когда внутри твердого тела протекает электрический ток, происходит химическая или эндотермическая реакция или же ядерное превращение. Все эти реакции происходят за счет внутренних источников тепловой энергии [1–3]. В инженерной практике большие трудности представляет собой получение точных приближенно-аналитических решений задач нестационарной теплопроводности с использованием классических методов под воздействием внутренних источников теплоты [4–5] (метод Фурье, функций Грина, или интегральных преобразований), так как решения, найденные такими методами, выражаются сложными функциональными зависимостями. Тогда как применение таких решений в практических расчетах крайне затруднено. В случае если мощность внутренних источников изменяется во времени, во многих случаях, классические методы вообще неприменимы.
При проектировании теплообменного оборудования, как правило, применяются полуэмпирические теории (являющиеся обобщением экспериментальных данных), позволяющие существенно упростить расчеты. Для более точных расчетов используют современные средства численного моделирования – программные комплексы Ansys, Comsol, OpenFoam и др. Однако их использование существенно ограничивается вычислительной мощностью ЭВМ. В связи с этим развитие также получили точные и приближенные аналитические методы математического моделирования процессов теплообмена и гидродинамики. Использование аналитических методов оправдано для решения краевых задач для теплообменных систем простой геометрической формы, без учета зависимости теплофизических свойств от температуры и др. Преимущество аналитических решений состоит в том, что они могут быть использованы при параметрическом анализе процесса, для решения обратных задач, параметрической идентификации.
В статье [1] представлен метод математического моделирования процесса переноса тепловой энергии без учета теплофизических параметров в пластине при граничных условиях I рода. Следуя представленному методу, решение задачи сводится к интегрированию обыкновенного дифференциального уравнения относительно плотности теплового потока на поверхности исследуемой области решения дифференциального уравнения в частных производных относительно температуры. Нелинейность задачи с переменными теплофизическими свойствами накладывает ряд трудностей для применения результатов на практике. Решение дифференциальных уравнений теплопроводности с зависящими от температуры теплофизическими свойствами среды представляет собой громоздкие алгебраические зависимости. С учетом вышесказанного разработка приближенно-аналитических методов решения нелинейных задач теплопроводности является весьма актуальной задачей. Покажем, что предложенный метод в [1] эффективен при решении задач нестационарной теплопроводности при нелинейности.
Цель исследования: исследовать и проанализировать влияние теплофизических параметров на температуру в пластине при граничных условиях I рода с переменными внутренними источниками тепла.
Материалы и методы исследования
В данной работе представлены результаты сравнения эффективности метода математического моделирования решения задач нестационарной теплопроводности [1], основанного на использовании дополнительных граничных условий и дополнительной искомой функции (или плотности теплового потока) и процесса теплообмена с переменными теплофизическими свойствами.
Без учета теплофизических параметров математический вид задачи (для половины пластины ввиду симметрии):
 (1)
(1)
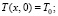 (2)
(2)
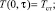 (3)
(3)
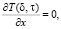 (4)
(4)
при τ > 0; 0 < x < δ; где Т, x, τ – температура, координата, время; a = λ/(cρ) – температуропроводность; ρ – плотность; λ – коэффициент теплопроводности; c – удельная теплоемкость; 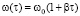 – удельная мощность внутреннего источника, ω0 – начальная мощность; T0, Tст – начальная температура, температура стенки; δ – половина толщины.
– удельная мощность внутреннего источника, ω0 – начальная мощность; T0, Tст – начальная температура, температура стенки; δ – половина толщины.
Задача (1)–(4) может быть представлена в виде [1]
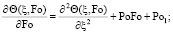 (5)
(5)
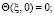 (6)
(6)
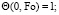 (7)
(7)
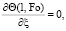 (8)
(8)
при Fo > 0; 0 < ξ < 1; где 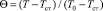 – безразмерная температура; ξ = x/δ – безразмерная координата;
– безразмерная температура; ξ = x/δ – безразмерная координата; 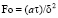 – критерий Фурье;
– критерий Фурье; 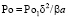 – критерий Померанцева;
– критерий Померанцева; 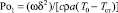 – начальное значение Померанцева в нулевой момент.
– начальное значение Померанцева в нулевой момент.
Согласно разработанному в [1] методу введем в рассмотрение новую искомую функцию времени
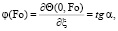 (9)
(9)
где α – угол между осью координат ξ и касательной к графику температуры в ξ = 0.
Тогда
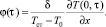
Согласно уравнению теплопроводности плотность теплового потока на поверхности пластины определяется выражением
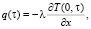
можно представить
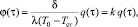
где k = const.
Решение задачи (5)–(8) отыскивается в виде
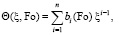 (10)
(10)
где bi(Fo) – коэффициенты, 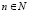 – натуральное число, соответствующее количеству членов (10).
– натуральное число, соответствующее количеству членов (10).
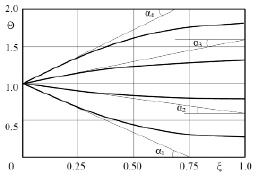
Рис. 1. Схема теплообмена
В первом приближении решение [1]
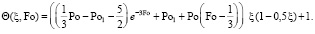 (11)
(11)
Новая функция на поверхности пластины определяется выражением
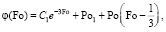 (12)
(12)
где C1 – константа интеграции, которая определяется из невязки условия.
Для нахождения решения во втором приближении потребуется увеличение степени (10). При определении коэффициентов bi будут использоваться новые дополнительные граничные условия. Четвертое граничное условие найдено после подстановки ξ = 0 в исходное уравнение. Пятое и шестое граничные условия найдены путем однократного дифференцирования исходного уравнения и постановкой значений координат ξ = 0 и ξ = 1 соответственно. После нахождения новых граничных условий составляется система шести алгебраических уравнений. Решая данную систему, находятся коэффициенты bi.
Во втором приближении решение получено в виде [1]
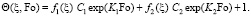 (13)
(13)
Во втором приближении новая искомая функция определяется выражением
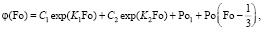 (14)
(14)
где K1 = 2,4633; K1 = 36,5370 при Po = 5; Po1 = 5.
В последующих приближениях для дальнейшего повышения точности требуется увеличивать число членов алгебраического полинома. Для отыскания решения в дальнейших приближениях потребуется вводить новые дополнительные граничные условия.
Общие формулы для их определения краевых граничных условий имеют следующий вид [1]
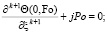
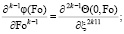
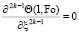
при j = 0, k > 3, j = 1, k ≤ 3, где k = 1, 2, 3 ... – номер выполняемого приближения.
Уравнение теплопроводности, которое учитывает теплофизические свойства среды, то есть зависимость свойств среды от температуры и нелинейную зависимость от температуры мощности внутренних источников, представлено выражением (15). В случае введения зависимости от температуры граничные условия (7)–(9) записываются в виде (16)–(18):
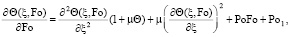 (15)
(15)
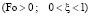
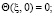 (16)
(16)
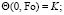 (17)
(17)
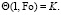 (18)
(18)
где μ – коэффициент теплопроводности; K – константа.
Результаты исследования и их обсуждение
На рис. 2, 3 представлены графики изменения 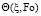 при различных значениях коэффициента μ.
при различных значениях коэффициента μ.
Результаты численного решения задачи (15)–(18) представлены на рис. 2, 3. Делаем вывод, что учет зависимости коэффициента теплопроводности от температуры приводит к существенному изменению температурной функции. В частности, при увеличении μ отмечается снижение температурных градиентов внутри тела.
На рис. 4 представлены графики новой искомой функции φ(Fo) по формуле (14). Из графика видно, что точность определения плотности теплового потока φ(Fo) значительно превышает точность определения безразмерной температуры относительно продольной координаты и безразмерного времени. Анализируя график на рис. 4, можно заключить, что в промежутке безразмерного времени 0,1 ≤ Fo < ∞ расхождение результатов плотности теплового потока составило около 4 %. Соответственно, решение задачи без учета нелинейности в работе [1] можно считать эффективным.
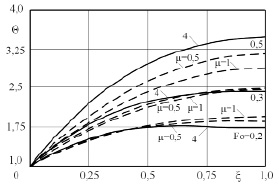
Рис. 2. Графики изменения температуры: – – – – численное решение с учетом нелинейности; –– – приближенное решение в четвертом приближении без учета нелинейности, при Po = 5; Po1 = 5
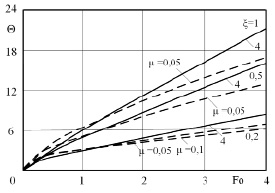
Рис. 3. Графики изменения температуры: – – – численное решение с учетом нелинейности; ––– – приближенное решение в четвертом приближении без учета нелинейности; при Po = 5; Po1 = 10
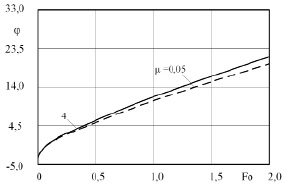
Рис. 4. Графики изменения плотности теплового потока φ(Fo). –––– – приближенное решение без учета нелинейности; – – – численное решение с учетом нелинейности; 4 – номер приближения; Po = 5; Po1 = 10
Анализируя рис. 4, можно сделать вывод, что в момент времени кода Fo = 0 значение плотности теплового потока φ(Fo) увеличивается до 10 уже в первом приближении.
Выводы
Целью данной статьи было показать влияние теплофизических параметров в бесконечно протяженной пластине на безразмерную температуру при граничных условиях I рода с внутренними источниками теплоты переменными во времени.
Показано, что расхождение результатов расчетов безразмерной температуры относительно безразмерного времени в бесконечно протяженной пластине с численным решением уравнения в промежутке времени 0,1 ≤ Fo < ∞ около 10 % и понижается при учете коэффициента μ.
Исследование выполнено при финансовой поддержке Совета по грантам Президента РФ в рамках научного проекта МК–2614.2019.8.


 science-review.ru
science-review.ru