Стержневыми называют системы, состоящие из прямолинейных стержней, соединённых в узлах [1]. По характеру соединения элементов в узлах различают системы с жесткими узлами, шарнирным соединением всех элементов и комбинированные. С точки зрения геометрии различают плоские и пространственные стержневые системы.
Фермами называют такие стержневые системы, которые при замене жестких узлов на шарнирные соединения остаются геометрически неизменяемыми, то есть такими, форму которых невозможно изменить без деформации материала. К ферменным конструкциям нагрузка прикладывается только в узлах, и в их элементах возникают только усилия растяжения-сжатия [2].
Ферменные конструкции широко распространены в качестве элементов зданий и сооружений. Такая популярность обусловлена рядом преимуществ:
экономичность – более низкий расход материалов по сравнению с другими строительными конструкциями;
универсальность – область применения ферменных конструкций очень широка и включает в себя мосты, стропильные системы зданий, краны и т.д.;
масштабируемость – длина ферменной конструкции может варьироваться от нескольких метров до нескольких километров.
В связи с этими характеристиками ферм их моделирование и расчет являются актуальными задачами проектирования строительных конструкций. Автоматизация решения этих задач ведёт к повышению эффективности проектирования, увеличению точности расчетов и снижению затрат.
Цель исследования: рассмотрение функционала и алгоритма работы программного модуля, выполняющего формирование геометрии двумерных ферменных конструкций для последующего моделирования. Данный программный модуль является компонентом сервиса SopromatGuru [3].
Материалы и методы исследования
Так как ферменные конструкции являются панельными, то есть состоят из множества идентичных или схожих по геометрии секций (панелей), существует возможность формирования модели такой конструкции параметрически с использованием относительных координат узлов при задании секции. Параметрами при таком моделировании являются итоговые размеры всей конструкции (высота и пролет фермы) и количество используемых секций.
Функционал рассматриваемого программного модуля предусматривает моделирование ферменных конструкций шести видов поясов и их подтипов в зависимости от используемой решетки (рис. 1).
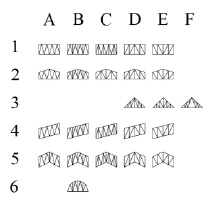
Рис. 1. Используемые в модуле схемы конструкций
Классификация используемых типов ферм [4]:
1) прямоугольная с параллельными по- ясами;
2) трапециевидная;
3) треугольная;
4) наклонная с параллельными поясами;
5) двууклонная;
6) полигональная.
Классификация используемых типов ре- шетки:
A. треугольная;
B. треугольная со стойками;
C. треугольная с подвесками;
D. раскосная с восходящими раскосами;
E. раскосная с нисходящими раскосами;
F. со шпренгелями.
В качестве языка программирования при разработке модуля использован язык JavaScript. В связи с этим модуль предоставляет широкие возможности для реализации облачных вычислений строительных конструкций в веб-интерфейсе [5].
В основе программного модуля лежит объектная модель, представляющая собой массив объектов, описывающих каждый из шести типов конструкций. В качестве параметров для всех типов конструкций выступают длина l и высота h. Для типов ферм 2, 4, 5 требуется задать также разность высот dh. Для каждого типа конструкции задан массив объектов, описывающих геометрию его подтипов: положение узлов и стержней, правила построения секций (четность, зеркальное отражение половин конструкций, использование разделителей).
Алгоритм программного модуля формирует по заданным параметрам массив абсолютных координат узлов всех стержней фермы. Этих данных достаточно для описания геометрии модели. Для полноценного задания модели конструкции в рамках модуля присутствуют следующие дополнительные возможности:
– задание шарнирных опор;
– задание шарниров на концах стержней;
– задание смещения левого опорного узла относительно начала координат на схеме;
– задание нагрузок на верхние узлы кон- струкции;
– группировка элементов для удобства последующей обработки.
Алгоритм работы модуля состоит из следующих операций:
1. Вычисление координат узлов для крайних вертикальных стержней конструкции, если они существуют для выбранного типа конструкции.
2. Вычисление ширины отдельных секций и координат узлов центрального опорного стержня типа конструкции 5.
3. Последовательное вычисление координат узлов каждой секции и формирование массива стержней.
4. Вычисление координат узлов для дополнительных вертикальных стержней между секциями, если это необходимо для выбранного подтипа конструкции.
5. Предварительная визуализация схемы конструкции средствами модуля.
6. Назначение дополнительных свойств.
7. Передача данных для построения схемы и расчета.
При интеграции модуля в веб-приложение для расчета двумерных стержневых конструкций выбор типа и подтипа схемы происходит в интерфейсе, представленном на рис. 2. Для ввода параметров конструкции используются числовые поля с возможностью инвертирования значений. При изменении типа фермы и вводе параметров происходит автоматическое перестроение предварительной схемы конструкции.

Рис. 2. Интерфейс задания основных параметров конструкции
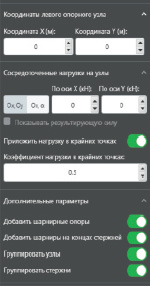
Рис. 3. Интерфейс задания дополнительных параметров конструкции
Для тонкой настройки дополнительных параметров фермы используются поля и переключатели (рис. 3).
Для иллюстрации работы модуля в рамках веб-приложения продемонстрируем построение и расчет полигональной конструкции длиной 25 м, высотой 9 м и состоящей из 6 секций (панелей). В узлах верхнего пояса данной конструкции по вертикали приложены сосредоточенные силы величиной 3 кН. Интерфейс модуля и результат построения схемы представлены на рис. 4. Расчет конструкции осуществляется методом конечных элементов [6].
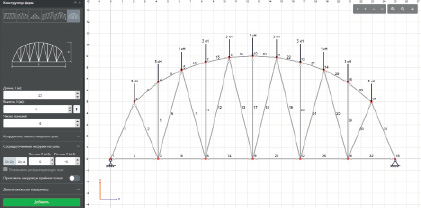
Рис. 4. Задание и визуализация схемы конструкции
Результаты исследования и их обсуждение
Значения опорных реакций и внутренних усилий рассчитанной конструкции представлены в табл. 1 и 2 соответственно. В табл. 1 R – вертикальная составляющая опорной реакции, H – горизонтальная составляющая опорной реакции, М – изгибающий момент.
Таблица 1
Значения опорных реакций
|
№ узла |
Тип опорного закрепления |
Значения |
|
1 |
Подвижный шарнир |
R1 = 16,5 (кН), H1 = 0 (кН), M1 = 0 (кН*м) |
|
18 |
Неподвижный шарнир |
R18 = 16,5 (кН), H18 = 0 (кН), M18 = 0 (кН*м) |
Таблица 2
Значения внутренних усилий в стержнях
|
№ стержня |
|Q, max| (кН) |
|N, max| (кН) |
|M, max| (кН*м) |
|
1 |
0 |
17,888 |
0 |
|
2 |
0 |
6,232 |
0 |
|
3 |
0 |
6,91 |
0 |
|
4 |
0 |
12,12 |
0 |
|
5 |
0 |
0,105 |
0 |
|
6 |
0 |
5,841 |
0 |
|
7 |
0 |
3,717 |
0 |
|
8 |
0 |
10,825 |
0 |
|
9 |
0 |
10,507 |
0 |
|
10 |
0 |
12,417 |
0 |
|
11 |
0 |
1,29 |
0 |
|
12 |
0 |
2,363 |
0 |
|
13 |
0 |
0,765 |
0 |
|
14 |
0 |
12,325 |
0 |
|
15 |
0 |
11,989 |
0 |
|
16 |
0 |
12,523 |
0 |
|
17 |
0 |
1,489 |
0 |
|
18 |
0 |
0,765 |
0 |
|
19 |
0 |
2,363 |
0 |
|
20 |
0 |
12,325 |
0 |
|
21 |
0 |
12,523 |
0 |
|
22 |
0 |
11,989 |
0 |
|
23 |
0 |
1,29 |
0 |
|
24 |
0 |
3,717 |
0 |
|
25 |
0 |
5,841 |
0 |
|
26 |
0 |
10,825 |
0 |
|
27 |
0 |
12,417 |
0 |
|
28 |
0 |
10,507 |
0 |
|
29 |
0 |
0,105 |
0 |
|
30 |
0 |
6,232 |
0 |
|
31 |
0 |
17,888 |
0 |
|
32 |
0 |
6,91 |
0 |
|
33 |
0 |
12,12 |
0 |
Полученная эпюра продольных сил представлена на рис. 5.
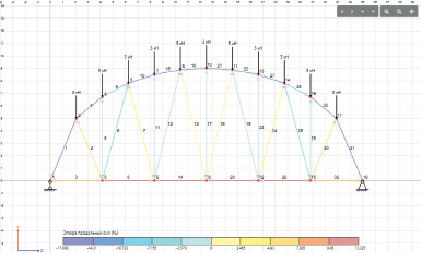
Рис. 5. Эпюра продольных сил
Заключение
Использование данного программного модуля в рамках средства для расчета стержневых конструкций позволяет упростить процесс моделирования и расчета сложных ферменных конструкций, снизить затраты времени и ресурсов на проектирование. Программный модуль предоставляет широкие возможности по заданию различных типов конструкций, приложению нагрузок и назначению свойств стержневой системы, что делает его полезным инструментом для инженеров-проектировщиков и студентов строительных специальностей.


 science-review.ru
science-review.ru