science-review.ru
В защищенных информационных и мобильных системах процедура персонификации личности (идентификация и аутентификация) является первым обязательным рубежом защиты. Для реализации этой процедуры в настоящее время все большее внимание уделяется биометрическим методам, обладающим рядом неоспоримых преимуществ [1]. Особой разновидностью биометрических методов персонификации личности является использование ее поведенческих (динамических) характеристик, представленных манерой подсознательного воспроизведения любого текста в трех модальностях: голосом [2–4], рукописью [5–7] или клавиатурным набором [8, 9]. Важным при этом является то, что произвольный текст может быть неограниченного объема и представлен на любом языке. По этой причине такая разновидность биометрии получила название текстонезависимой биометрии. Ее преимуществами является высокая защита от атак воспроизведения текста, сравнительно невысокие затраты на ее реализацию (преимущественно программную). Недостаток, – бо?льшая продолжительность процедуры персонификации, обусловленная необходимостью сопоставления текстов с биометрическими эталонами большого объема. Кроме того, использование текстонезависимой биометрии связано с решением ряда проблем, связанных с оптимальным представлением эталонов образцов текста различной модальности, выбором необходимого объема образцов, своевременным определением момента принятия решения «свой – чужой» при персонификации личности.
Вместе с тем использование текстонезависимой биометрии не ограничивается исключительно задачами персонификации личности при входе в информационные и мобильные системы. Более перспективным направлением ее применения является скрытный мониторинг работы пользователей в уже ранее легально открытых ими информационных и мобильных системах. К таким задачам относятся, в частности [1]: скрытная непрерывная клавиатурная верификации работающих пользователей, исключающая их подмену в ранее легально открытых системах; скрытное выявление легальных пользователей (инсайдеров), осуществляющих неправомерные действия в системах, путем установления отклонений их клавиатурного почерка от нормы, вызванных незаконными действиями (психофизический эффект); открытое или скрытное выявление операторов, имеющих отклонение своего текущего психофизического состояния от нормы, актуальное в системах с большой ценой ошибки оператора; выявление личностей, поставляющих ложную информацию в вопрос-ответных процедурах (иная реализация детектора лжи) и другие задачи.
В текстонезависимой динамической биометрии образы личностей представлены периодическими сигналами. Традиционным подходом к решению задачи распознавания таких сигналов является предварительный перевод их в частотную область путем разложения в какой-либо ряд: Фурье, Уолша, Хаара и др. Коэффициенты разложений выступают в качестве контролируемых информационных параметров, и задача распознавания образов решается уже в формате статического представления [1].
В данной работе предлагается иной подход к распознаванию сигналов текстонезависимой динамической биометрии. Он заключается в первичном временном квантовании исходного сигнала и последующем его вторичном квантовании, позволяющем выделить группы соседних отсчетов сигнала первичного квантования одинакового размера. Выделенные группы представляются далее многомерными векторами в Евклидовом пространстве и трактуются как информационные единицы анализируемого биометрического сигнала. Такой подход имитирует принцип обработки данных в искусственных иммунных системах (ИИС) [10, 11]. Верификация динамической биометрии личности осуществляется далее путем кластеризации указанных многомерных векторов с помощью обученной нейронной сети Кохонена и последующего статистического анализа ее выходных данных.
Размерность сигналов текстонезависимой динамической биометрии зависит от модальности. В голосовых системах сигналы одномерные, в рукописных онлайновых системах мерность определяется числом квазинепрерывных характеристик взаимного положения пера и графического планшета (обычно от двух до восьми степеней свободы), в клавиатурных системах мерность определяется способом представления исходных данных. Поэтому в общем случае сигналы текстонезависимой динамической биометрии следует считать многомерными: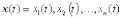 
. Далее на этапе предварительной обработки они оцифровываются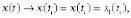 
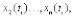i = 1, 2, ... и приводятся к единому масштабу по всем компонентам. В реальном масштабе времени текст может содержать длительные паузы, не обусловленные индивидуальным характером его воспроизведения данной личностью, поэтому такие паузы исключаются из анализа. При голосовом воспроизведении текста из него исключатся также неинформативные фонемы шипящих звуков.
Сигнал x(ti), i = 1, 2, ... рассматривается далее как последовательность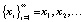 
элементов, представленных векторами признаков: xi.
В динамической биометрии выявлен принципиально важный феномен, который заключается в том, что личностные особенности воспроизведения определенного текста наблюдаются в большей степени не в одиночных символах, а в группах последовательно расположенных символов, несущих индивидуальную морфологическую окраску слов. Это позволяет существенно повысить точность биометрической верификации личности [1].
Для воспроизведения указанного феномена последовательность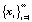 
расчленяется на фрагменты одинакового размера по r отсчетов в каждом фрагменте 
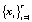. Каждый фрагмент 
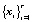трактуется далее как элемент новой последовательности 
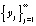, содержащий r векторов xi исходной последовательности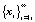 
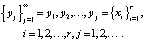
Для использования указанного феномена последовательность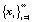 
расчленяется на фрагменты 
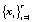одинакового размера по r отсчетов в каждом фрагменте. Результатом будет новая последовательность 
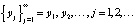, каждый элемент yj которой содержит r векторов xi исходной последовательности 
:
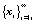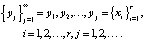
При этом элементы yj представляют собой s-мерные вектора yj, содержащие s = n×r компонент:
Последовательность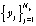 
, ограниченная Ny элементами, представляет биометрический эталон личности.
В итоге общее распределение динамических биометрических данных личности будет представлено множеством кластеров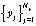 
s-мерных векторов yj, в пространстве признаков Es. При этом каждый кластер будет содержать фрагменты биометрии, специфичные по воспроизведению данной личностью.
Режим верификации предполагает возможность сопоставления предъявленного образца биометрии априори легитимной личности соответствующему ей биометрическому эталону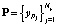 
. По результатам сопоставления принимается верификационное решение «свой – чужой». Анализ минимаксных значений 
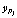по координатам s позволяет сузить потенциальное пространство признаков 
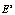в рабочее пространство 
.
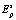Обучение системы осуществляется на основе самоорганизующейся нейронной сети Кохонена (или какой-либо последующей ее модификации) [12–14]. Цель обучения – кластеризация пространства признаков 
для эталона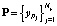 
. Результатом кластеризации будет совокупность кластеров k = 1, 2, …, l. Число кластеров l выбирается из эмпирических соображений, связанных с приемлемой точностью и вычислительной сложностью воспроизведения сети.
Простейший вариант схемы нейронной сети Кохонена для решения поставленной задачи приведен на рисунке.
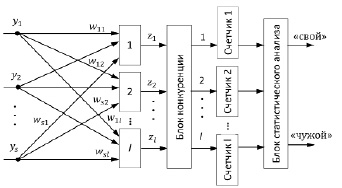
Схема нейронной сети Кохонена
Нейроны сети Кохонена реализуют операцию взвешенного суммирования:
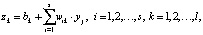
где yj компоненты входного вектора yj; zk – выходы нейронов; bk – пороги нейронов; wik – веса нейронов.
Выходные сигналы нейронов подвергаются конкуренции по правилу «победитель получает всё». Для этого выходные сигналы нейронов сравниваются и максимальный из них обращается в 1, остальные обращаются в 0. Если максимум возникает одновременно на выходах нескольких нейронов, то все эти выходные сигналы также обращаются в 1.
Счетчики на выходах блока конкуренции служат для подсчета единиц на выходах сети при предъявлении входной последовательности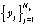 
.
Нейрон становится победителем в конкуренции, если для него выполняется соот- ношение
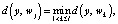
где j – номер нейрона-победителя; d(y, wj) – расстояние между векторами y и w в метрике Евклида
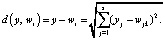
Корректировка весов «выигравшего» нейрона осуществляется по правилу Кохонена
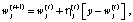
где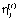 
– коэффициент скорости обучения j-нейрона в t-цикле обучения.
Нейронная сеть обучается путем поочередной подачи на ее входы элементов эталонной последовательности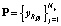 
. После обучения пространство 
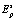будет расчленено на кластеры, представляющие собой s-мерные многогранники Вороного – Дирихле, стороны которых являются фрагментами секущих пространство 
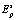гиперплоскостей. Центры кластеров представлены векторами, соответствующими столбцам весовой матрицы сети.
За один цикл обучения, соответствующий предъявлению всех Ny единиц входных данных P, на каждом из k = 1, 2, …, l выходах сети будет появляться nkP единиц. Величины nkP можно считать случайными величинами, зависящими от структуры входной последовательности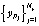 
. Таким образом, общая картина возбуждений сети будет представлена системой случайных величин nkP.
Длительность обучения в системе определяется одним циклом прогона последовательности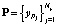 
.
После обучения нейронная сеть подвергается тестированию, чтобы зафиксировать конечный результат кластеризации пространства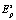 
, необходимый для последующего статистического анализа.
При тестировании через обученную сеть пропускается последовательность эталона P и по каждому k-выходу сети подсчитывается количество единиц nkP. Далее рассчитывается вероятность появления образов в каждом кластере для эталонной последовательности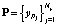 
:
.
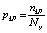Математическое ожидание количества единиц в k-кластере сети будет равно
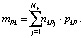
Математическое ожидание mP всей картины возбуждений сети для эталона P будет равно сумме математических ожиданий количества единиц в каждом k-кластере:
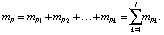
Полученный результат mP трактуется как статистическая оценка всей картины кластеризации пространства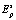 
для эталона P. На этом этап тестирования сети заканчивается, и она готова для верификации биометрических данных.
В рабочем режиме через обученную сеть пропускается последовательность априори неизвестной личности X того же размера, что и эталонная –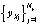 
и делается оценка математического ожидания mx картины кластеризации пространства 
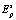на основе рассчитанных ранее вероятностей появления выходных образов в каждом кластере для эталона P:
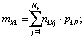
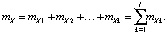
Картина кластеризации пространства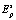 
, представленная суммарным математическим ожиданием mX будет характеризовать биометрию личности X. Если анализируемая биометрия принадлежит легальной личности, то mX будет близка к величине mP. Для любой другой личности X она будет существенно отличаться от mP.
Для принятия верификационного решения, исходя из допустимой величины ошибки первого рода (недопуск «своего»), устанавливается пороговая величина невязки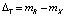 
, на основании которой неизвестную личность X следует признать «своим» XC или «чужим» XЧ:
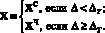
Заключение
Однотипное представление сигналов динамической биометрии разной модальности позволило предложить общий подход к реализации процедуры верификации личности на основе сочетания принципов представления данных, характерных для в ИИС и принципов их кластеризации в самоорганизующихся нейронных сетях. Перспектива применения такого подхода определяется стремительным ростом производительности вычислительных средств, открывающим возможность эффективно применять ИИС и самоорганизующиеся нейронные сети больших размерностей для решения таких сложных задач.