Для описания процесса эволюции динамических систем часто используются точечные отображения [1]. Ими, например, можно описать значения параметров системы через равные промежутки времени – таким образом, процесс изменения параметров из непрерывного превращается в дискретный (точечный), а подбирая достаточно высокую частоту дискретизации, функцию изменения параметров можно описать очень точно. Такой метод идеально подходит при использовании вычислительной техники, а также позволяет описывать сложные процессы достаточно простыми итерационными зависимостями [2].
На заре развития данного метода он не применялся для описания реальных физических явлений и был чисто абстрактным. Однако оказалось, что различные типы точечных отображений имеют явное воплощение в природных явлениях и не хуже, чем используемые до этого системы дифференциальных уравнений, описывают системы, параметры которых меняются с течением времени. Более того, были открыты многие доселе неизвестные особенности многих систем, в частности их способность при определённых параметрах проявлять упорядоченное поведение, а при других – хаотичное. Такой хаос назвали детерминированным, так как система хоть и демонстрирует неупорядоченное поведение, всё же при этом развивается, эволюционирует согласно заданным законам. Исследованию динамических систем посвящён дополняемый данной статьёй цикл публикаций авторов [3, 4].
Цель описываемого исследования состоит в создании разных типов программной реализации на языке Python [5] метода точечного отображения для получения графического изображения эволюции как при определённых пользователем начальных параметрах системы, так и для формирования общей картины, наглядно показывающей области устойчивости (периодичности) и хаоса при варьируемых значениях параметров системы. Поставленные задачи решались на примере одной из динамических систем, эволюция которой определяется двумя параметрами – двумерного точечного отображения Эно. Также необходимо представить примеры расчёта с помощью разработанных программ.
Материалы и методы исследования
Так как точечные отображения дискретны, то вместо численного обозначения рассматриваемых моментов времени можно использовать просто номер рассматриваемой итерации вычислений (подобно тому, как данный процесс осуществляется в АЦП – аналого-цифровом преобразователе [6]). Следует отметить, что согласно современным представлениям, время – чисто абстрактное понятие, используемое только для удобства существования человека. Используемые единицы времени связаны с цикличностью процессов в Солнечной системе, а при рассмотрении универсальных законов Вселенной часто более логичным является применение понятия итерации.
Рассмотрим двухмерную дискретную динамическую систему, каждое последующее состояние которой зависит от предыдущего (каждая последующая итерация зависит от предыдущей). Такую систему можно описать очень простыми зависимостями
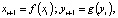
где xi, yi – координаты на i-й итерации, а xi+1, yi+1 – координаты на следующей итерации.
Несмотря на простоту данного описания, картина, формируемая координатами x, y на плоскости, с увеличением количества итераций, может быть как упорядоченной, так и хаотичной.
Рассмотрим один из видов представленных итерационных зависимостей, называемый точечным отображением Эно (на самом деле таких отображений много и каждое из них применимо для описания определённого класса физических процессов, но принципы вычислений являются общими). Итак, функции отображения Эно (Henon map) выглядят следующим образом:
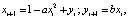
где а, b – постоянные множители.
Система Эно может описывать физический процесс движения массы, подвергаемой импульсным толчкам, при наличии рассеяния энергии [7].
Функция первой разрабатываемой на языке Python программы заключается в выводе траектории эволюции системы Эно при заданных а, b и количестве итераций. При реализации графической интерпретации системы формирование её траектории становится наглядным.
Программа на языке Python для построения отображения Эно состоит из следующих частей:
1. Импорт модуля Мatplotlib.pyplot для вывода графики.
2. Присвоение начальных значений координат х и у. Для примера они взяты равными по 1, хотя это не имеет определяющего значения для получающегося результата.
3. Присвоение значений коэффициентов а и b. Для примера приняты a = 1,4, b = 0,3, которые по теории соответствуют хаотичной формируемой картине [8].
4. Выбрано число итераций (вычисляемых точек). Для обеспечения плавности и чёткости картины это значение принято равным 10 тысячам.
5. Организация цикла вычисления координат х, у точек согласно вышеприведённым формулам. После вычисления координаты каждой точки она выводится в буфер экрана с помощью графической функции scatter, с заданием желаемого размера и цвета.
6. В буфер экрана выводятся обозначения осей координат, после чего файл сформированного изображения сохраняется командой savefig с выбором имени, формата и разрешения файла. Возможен вывод изображения в графическое окно с помощью команды show.
Эта и все описанные в данной статье программы приведены для изучения на сайте одного из авторов [9].
Полученное с помощью программы двухмерное отображение Эно для a = 1,4, b = 0,3 приведено на рис. 1.
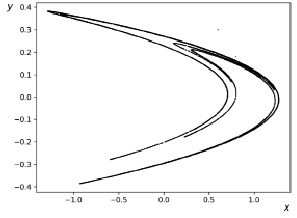
Рис. 1. Формируемое программой двухмерное отображение Эно в зоне хаоса
Точечный график отображает типичную картину детерминированного хаоса – кривые, на которых последовательно размещаются точки, строго не определены, но являются достаточно характерными и тяготеют к определённым центрам притяжения – аттракторам. Если построить отображение для коэффициентов а и b, при которых поведение системы устойчиво (например, при a = 0,5, b = -0,5), то на графике будут присутствовать лишь одна или несколько дискретных точек, причём и для количества итераций, равного 100, и для 100 тысяч количество дискретных точек будет одинаково. То есть, пройдя непродолжительный цикл дискретных состояний, система возвращается всё к одному и тому же первоначальному состоянию.
Вторая разработанная программа представляет отображение Эно в виде точечного 3D графика, по вертикальной оси которого z откладывается номер итерации. В данном случае в начале описанного выше алгоритма необходимо добавить импорт функции Axes3D библиотеки mpl_toolkits.mplot3d, а также создавать и заполнять отдельные массивы координат х, у, z. По заполненным массивам в конце программы также строится точечный график с помощью команды scatter путём перебора координат всех точек (с выбором их размера и цвета) в двух вложенных циклах для координат x и у. Затем указываются подписи осей и график выводится на экран или в файл.
Пример получаемого 3D отображения Эно при тех же коэффициентах a и b, что и в первом примере, приведён на рис. 2.
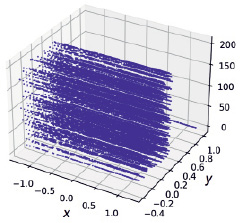
Рис. 2. Отображение Эно на точечном 3D графике
На представленном рисунке более ясно, чем на рис. 1, видна последовательность добавления точек на каждой итерации. Отчётливо заметно, что положение точек для выбранных a и b хаотично. В данном случае для большей наглядности использовано только 200 первых точек отображения. Кроме того, осуществление вывода в 3D формате большого количества точек на экран связано с сильной загрузкой видеобуфера, и изображение на экране очень медленно реагирует на вращение при попытке его изучения с разных сторон. Однако при выводе графики в файл никаких особенностей не отмечается.
На следующем этапе разрабатывалась программа для осуществления более глубокого исследования свойств отображения Эно не только при отдельных заданных (дискретных) коэффициентах отображения a и b, а при изменении этих параметров в широком диапазоне. В этом случае в качестве координат выводимого графика выступают сами коэффициенты a и b, а цвет точек графика показывает период повторения отображения (количество итераций, через которое картина при устойчивом процессе возвращается к первоначальной). Также на таком графике отображаются участки хаотичного поведения системы и участки, на которых координаты x, y при заданном количестве итераций уходят в бесконечность (быстро удаляются от первоначальных точек) – этот процесс называется слоением к бесконечности [10].
Если после некоторого количества итераций n точка (x, y) переходит сама в себя, то такая система является устойчивой. Такое количество итераций называется циклом системы, а сама точка называется неподвижной точкой кратности n. Длительность цикла n можно определить следующим образом: создать последовательность нескольких предпоследних значений последовательности координат (чаще всего берут 8) и сравнивать их с самым последним значением.
Так как мы оперируем двумя координатами, то удобнее всего не сравнивать отдельно значения х и у, а сравнивать объединённые в комплекс значения:
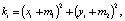
где m1 и m2 – постоянные, необходимые для предотвращения повторений ki внутри цикла.
Описанным способом мы можем исследовать устойчивость системы Эно с определёнными коэффициентами a, b. С помощью организации цикличных вычислений можно проделать ту же операцию для значений a, b, изменяющихся с определённым малым шагом в определённых пределах. Сопоставив каждому вычисленному значению цикла свой цвет точки, получим диаграмму, называемую картой динамических режимов системы.
Рассмотрим этапы реализации алгоритма получения такой карты на языке Python:
1. Импорт модуля Мatplotlib.pyplot для вывода графики.
2. Присвоение значений для нижних и верхних пределов изменения коэффициентов a и b.
3. Присвоение значения переменной ε, указывающей допустимую разницу между сравниваемыми значениями k1 (на самой последней итерации) и последовательно k2…k8. Задание предельного количества вычисляемых итераций (реально карта динамических режимов не меняется при значении 100, однако с запасом принято 1000 итераций).
4. Создание основной функции программы, предназначенной для выявления цикличности итераций и окрашивания точки, соответствующей каждому сочетанию коэффициентов а и b, задаваемых в качестве входных значений основной функции, наряду с переменными, приведёнными в п. 3. Вычисления отображения осуществляются как в первой описанной программе, но сохраняются только 8 последних значений k, зависящих от координат х, у (формула для k приведена выше). Если разница |k1-k2|< ε, то считаем, что цикл равен одной итерации и окрашиваем соответствующую точку в первый цвет радуги (красный). Если цикл равен двум итерациям, то цвет точки оранжевый и т.д. Для цикла, равного 7, цвет точки фиолетовый. Если цикл больше 7, то считаем, что переход между итерациями хаотичный, и такая точка окрашивается в чёрный цвет. Если k уходит в бесконечность (реально задано, что на какой-либо итерации превышает 1010), то вычисление итерационного цикла прерывается, а цвет точки считается белым.
5. В двух вложенных циклах осуществляется перебор значений коэффициентов а и b с заданным шагом (оказалось, что достаточно шага, равного примерно 1/500 от соответствующего значения коэффициента – при меньшем шаге длительность вычислений на компьютере средней конфигурации превышает сутки) и определение цвета точек карты динамических режимов системы. При этом для наблюдения за ходом процесса вычислений текущее значение a (изменение которого реализовано во внешнем цикле) выводится на экран.
6. Вывод точечного графика на экран или в файл с помощью команд, описанных в п. 6 алгоритма первой программы (для получения двухмерного отображения Эно).
Полученные с помощью третьей разработанной программы карты динамических режимов системы Эно при разных границах изменения коэффициентов a и b и значении допустимого отклонения ε = 0.01 приведены на рис. 3.
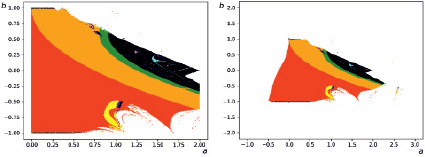
Рис. 3. Карты динамических режимов отображения Эно
Результаты исследования и их обсуждение
По рис. 3 ясно видны зоны устойчивого (различные цвета радуги) и хаотичного поведения отображения Эно. Зоны устойчивости точечного отображения Эно не простираются дальше a = -0,5–2.5, b = -1–1. При этом зоны устойчивости с разной цикличностью не располагаются по порядку, а причудливо перемешаны.
Также по проведённым с помощью последней программы исследованиям можно сделать вывод, что при меньшем допускаемом отклонении численного значения коэффициента цикличности k (параметра ε) получается более чёткий график, с меньшим количеством «вкраплений» точек устойчивости в зоны хаоса. Также чётко видно белые зоны, в которых итерации быстро уходят в бесконечность, то есть функция системы является расходящейся. В таком случае ни о какой устойчивости также не может идти и речи.
В зонах изменения коэффициентов отображения а и b, формируемых точками цветов радуги, при которых система постоянно возвращается в первоначальное состояние, с помощью созданных первой и второй программ можно найти координаты х, у точек, имеющих эти устойчивые значения.
Созданную методику, алгоритмы и доступные всем желающим коды трёх разработанных программ для построения характеристик точечных отображений Эно можно легко модифицировать (изменив только две итерационные зависимости) и использовать для исследования других двухмерных точечных отображений. Это может помочь при создании численных моделей реальных физических процессов на основе современных методов исследования.
Заключение
Таким образом, в результате проведённого исследования разработаны методы языка Python и программы, призванные помочь в исследовании точечных отображений, и теории хаоса, в которых они чаще всего используются. В частности, рассмотрены варианты этих программ для популярного при обучении основам исследования динамических систем точечного отображения Эно.
На следующем этапе исследований планируется использование написанных авторами программных кодов в качестве базы для создания сравнительного обзора использования других типов точечных отображений для создания совершенных численных моделей функционирования реальных физических систем и протекания динамических процессов в различных отраслях научных разработок.


 science-review.ru
science-review.ru