Ниже приведены методы моделирования, потенциально применимые к моделированию тепловой карты криоконсервированных продуктов крови во время дефростации.
С целью решения обыкновенных дифференциальных уравнений и систем дифференциальных уравнений используются численные методы решения, в частности метод Эйлера [1]. Данный метод, основанный на аппроксимации интегральной кривой кусочно-линейной функцией, относится к явным и является одношаговым методом первого порядка [2]. Обычно для упрощения метода Эйлера используется разбиение на четыре шага.
1. Явный метод Эйлера
Во-первых, вводится расчетная сетка. Часто сетка является равномерной, то есть имеет одинаковое расстояние между узлами tn и tn+1, что показано в формуле
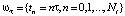 . (1)
. (1)
Во-вторых, предполагается, что уравнение выполнено в узлах сетки:
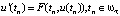 . (2)
. (2)
В-третьих, необходимо заменить производные конечными разностями. С этой целью требуется определить основные формулы, а также методы аппроксимации, так как производные могут быть аппроксимированы конечными разностями. Подход заключается в использовании определения производной
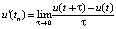 . (3)
. (3)
Чтобы не устремлять шаг сетки к нулю, необходимо использовать малый шаг ττ, который даст численное приближение u’(tn):
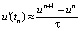 . (4)
. (4)
В научной литературе приведенная аппроксимация имеет первый порядок по τ и именуется как разностная производная вперед O(τ). После чего необходимо использовать аппроксимацию производной. Таким образом, определен явный метод Эйлера:
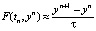 . (5)
. (5)
В-четвертых, необходимо формирование численного алгоритма. Из выше представленного уравнения (5) следует, что необходимо определить значение yn для того, чтобы решить уравнение относительно yn+1 и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое tn+1:
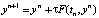 . (6)
. (6)
При условии наличия начального значения y0 = u0 возможно использование (6) для нахождения решений на последующих временных слоях.
2. Неявный метод Эйлера
С целью построения неявного метода Эйлера [3] необходимо установить значение функции F на новом временном слое (7), так как вероятность наличия неопределенных значений yn+1 равноценна в левой и правой частях разностного уравнения. Иными словами, данный метод можно рассматривать как некоторое усложнение явного метода Эйлера [4, 5].
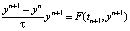 . (7)
. (7)
3. Метод конечных разностей и элементов
Метод решения дифференциальных уравнений с частными производными, основанный на замене производных разностными схемами, в свою очередь, представляющими собой сеточные методы, принято называть методом конечных разностей (МРК) [6, 7]. В свою очередь, при решении задач комплекса научных дисциплин, ставящих своей целью решение физических проблем для технологических или практических применений, необходимо решать дифференциальные уравнения с частными производными. Численным методом решения таких уравнений, в том числе интегральных, является метод конечных элементов (МКЭ) [8, 9].
С целью реализации данного метода для решения дифференциального уравнения необходимо его представление в двух формах: конечно-разностной форме и частных производных. Иными словами, необходимо осуществить переход к дискретной конечно-разностной сетке, чаще встречающемуся в научной литературе как дискретное пространство функций [10], реализуемое за счет перехода от непрерывного пространства. Эквивалентная формула, приведенная в (8), по аргументу x реализует определение производной от непрерывной функции u.
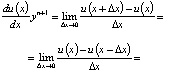
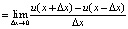 . (8)
. (8)
Вышеописанные физические свойства относятся к свойствам физической системы и ее непрерывного математического представления, связанного с причинностью, положительностью, обратимостью, согласованностью и консервативностью. Свойства системы определяются для решения эллиптической задачи методом конечных разностей на базе сетки в расчетной области, после чего необходимо определить разностную схему, в том числе для каждого узла сетки. С цель получения системы линейных алгебраических уравнений и определения апроксимальных приближенных значений решения в узлах схемы, необходимо учесть краевые условия. Следует отметить, что размер шага сетки определяется следующим соотношением 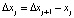 , так как производные и другие члены уравнения, которые входят в дифференциальные уравнения, являются частью конечно-разностных выражений. В таблице приведено сравнение достоинств различных численных методов таких уравнений.
, так как производные и другие члены уравнения, которые входят в дифференциальные уравнения, являются частью конечно-разностных выражений. В таблице приведено сравнение достоинств различных численных методов таких уравнений.
Сравнение МКР и МКЭ
|
Достоинства МКР |
Достоинства МКЭ |
|
- Высокая скорость построения разностной схемы для простых задач |
- Проекционность и устойчивость метода; - возможность работы с геометрически (более) сложными областями; - возможность определения значения в любой точке на базе сформированного сплайна |
Под расчетной сеткой понимается разбиение области на ячейки или дискретные подмножества точек, которые в свою очередь соединены непересекаемыми отрезками. В том случае, если расчетная сетка является структурированной и если она отображается на прямоугольной сетке в единичном кубе, то такая сетка является регулярной. Следует отметить необходимость сохранения порядка узлов для такой сетки. В противном случае структурированная сетка является равномерной и имеет постоянный шаг. Такие сетки принято называть неравномерными и подразделять на декартовы, имеющие прямоугольные и (или) криволинейные формы. Расчетные сетки, не попадающие под вышеописанное описание, считаются неструктурированными [11]. Среди преимуществ неструктурированных сеток можно отметить простоту их построения в областях, имеющих произвольную геометрию и, как следствие, низкую потенциальную точность решений.
Целью настоящей статьи является обзор методов моделирования, потенциально применимых к температурному картированию процесса дефростации, а также решение уравнения теплопроводности для одномерного и двумерного случаев. Полученные данные планируется использовать для создания математической модели процесса размораживания продуктов крови.
Материалы и методы исследования
Применительно к задаче моделирования тепловой карты криоконсервированных продуктов крови при дефростации, необходимо решить задачу теплопроводности. Таким образом, рассмотрим нормализованное уравнение теплопроводности в одном измерении с однородными граничными условиями Дирихле (9), где (10) – граничное условие, а (11) – начальное состояние.
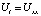 ; (9)
; (9)
 ; (10)
; (10)
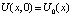 . (11)
. (11)
Один из способов численного решения этого уравнения – аппроксимировать все производные конечными разностями. Разделим область в пространстве сеткой x0,.....,xj, во время t0,.....,tN используя сетку. В случае однородного разделения как в пространстве, так и во времени разница между двумя последовательными точками пространства будет h, а между двумя последовательными моментами времени будет k. В таком случае точки (12) будут представлять собой численное приближение u(xj, tn).
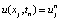 . (12)
. (12)
1. Явный метод Эйлера
Использование разницы вперед во времени tn и центральная разность второго порядка для пространственной производной в положении xj получаем рекуррентное уравнение (13).
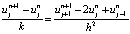 . (13)
. (13)
Формула (13) представляет собой явный метод решения одномерного уравнения теплопроводности. Необходимо получить 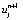 от других значений таким образом:
от других значений таким образом:
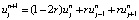 ,
,
где
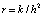 . (14)
. (14)
Рекуррентным соотношением (14) и определенными значениями в момент времени n формируются соответствующие значения вовремя n +1. В данном случае, а 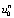 и
и 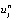 необходимо заменить граничными условиями, в приведенном примере они равны 0. Явный метод численно устойчив и сходится, когда r ≤ 1/2, а численные ошибки пропорциональны шагу по времени и квадрату шага по пространству
необходимо заменить граничными условиями, в приведенном примере они равны 0. Явный метод численно устойчив и сходится, когда r ≤ 1/2, а численные ошибки пропорциональны шагу по времени и квадрату шага по пространству 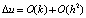 .
.
2. Неявный метод Эйлера
По сравнении с явным методом Эйлера, неявный метод является численно более интенсивным, ввиду необходимости решения на каждом шаге, определенном фиксированным интервалом времени, систем числовых уравнений, что ведет к образованию линейных по временному шагу ошибок, в свою очередь квадратичных по пространственному шагу 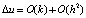 .
.
В уравнении (15) показано решение одномерного уравнения теплопроводности 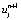 , определяемого из уравнения (13). С целью определения центральной разности для пространственной производной xj (второго порядка) при решении уравнения (15) необходимо использование обратной разницы во времени tn+1.
, определяемого из уравнения (13). С целью определения центральной разности для пространственной производной xj (второго порядка) при решении уравнения (15) необходимо использование обратной разницы во времени tn+1.
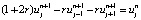 . (15)
. (15)
3. Сравнение методов конечных разностей
По способу выбора сетки, связывающих значения неизвестной функции в узлах сетки, а также по правилам формирования уравнений различают аналитические методы для решения задач, основанные на численных методах, позволяющих реализовать конкретное числовое описание (или модель) протекающего физического процесса. Однако такое числовое описание (модели) не позволяет судить о каких-либо качественных особенностях моделируемого или исследуемого процесса, так как численное решение задачи математической физики предполагает некоторую пространственно-временную область и ее приближенный дискретный аналог.
Для целей численного решения уравнения теплопроводности, а также аналогичных уравнений, формализованных в виде частных производных, возможно использование вышеописанных методов, к коим относится метод Кранка – Николсона, представляющий собой метод конечных разностей и являющийся методом второго порядка относительно временной шкалы [12, 13].
Следует отметить, что допуском явной схемы является меньшая точность и высокая трудоемкость, сопряженная с высокой нестабильностью, ввиду требовательности данной схемы к большому объему вычислений, в частности применительно к решению методом неявной схемой для больших временных шагов. Таким образом, решения, полученные с использованием вышеописанного метода, применительно к аппроксимации уравнения теплопроводности, показаны на рис. 1.

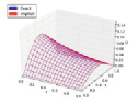
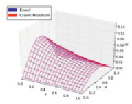
а) б) в)
Рис. 1. Аппроксимация уравнения теплопроводности на базе методов конечных разностей следующими схемами: а) явный метод; б) неявный метод; в) метод Кранка – Никольсона
С целью определения температуры, определенной в каждом узле сетки локальной характеристикой, необходимо получить систему линейных алгебраических уравнений на базе аппроксимации или замены частных производных дифференциального уравнения конечными разностями [14], так как при формализации алгебраических систем необходимо добиться высокого качества аппроксимации и в то же время эффективного устойчивого решения. Иными словами, конечноразностные аппроксимации используются как замена производных в дифференциальном уравнении.
Уменьшение расстояния между соседними узлами системы и увеличение их количества, возникающее при дискретизации, связывающее значения искомой величины в узлах сетки и позволяющее заменить дифференциальное уравнение, а также краевые условия на близлежащих узлах, является главным принципом, на котором построен метод конечных разностей. Однако вкупе с расположением узлов слоями по переменным данный метод может накладывать ограничения, связанные со структурой сетки, что в простых ситуациях (например, при решении задачи с неподвижными границами) ведет к изменению диапазона времени t, не связанному с изменением переменных, определенных в пространственных координатах x, y, z. С целью формирования уравнений прямоугольной сетки на базе времени, а также одной пространственной координате на рис. 2, а, показана разностная схема, применяемая для формирования таких уравнений.

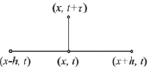
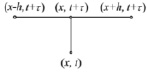
а) б) в)
Рис. 2. Метод конечных разностей: а) разностная схема метода конечных разностей; б) шаблон явной схемы для уравнения теплопроводности; в) шаблон неявной схемы для уравнения теплопроводности
На рис. 2, б и в, показаны шаблоны явной и неявной схемы для решения уравнений теплопроводности. Шаблон – это совокупность узлов сетки, значения в которых используются при аппроксимации дифференциального оператора.
Результаты исследования и их обсуждение
1. Применение метода конечных разностей для решения одномерного уравнения теплопроводности.
Дифференциальное уравнение с постоянной температурой по оси Oy и Oz при следующих условия будет иметь вид (16). T0 – начальная температура (внутри пластины отсутствуют любые источники тепловыделения), Tл – постоянная температура, поддерживаемая на одной границе пластины. Вышеуказанные условия представляют собой задачу анализа теплопередачи через плоскую бесконечной длины пластину, являющуюся также эквивалентом изолированного стержня [15, 16] и представленную на рис. 3, а.
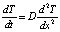 . (16)
. (16)
Где следующие начальные условия (17):
- температура по всей плоскости T(t = 0, x) = 0;
- температура в начале стержня T(t > x = = 0) = 10;
- (17).
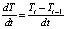 ;
;
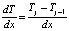 ; (17)
; (17)
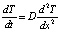 .
.
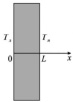
а) б)
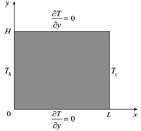
Рис. 3. Визуализация условий задачи теплопередачи: а) для решения одномерного уравнения теплопроводности; б) для решения двумерного уравнения теплопроводности
а) б)
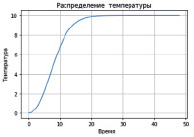
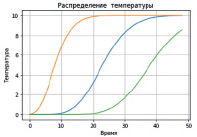
Рис. 4. Графики распределения температур: а) нагрев стержня в точке 10; б) желтый – зависимость температуры от времени в точке 10, синий – зависимость температуры от времени в точке 25, зеленый – зависимость температуры от времени в точке 40
а) б)
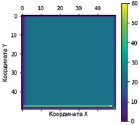
Рис. 5. Распределение температуры по поверхности пластинки: а) за 100 с; б) за 500 с
Результат вычислений – график в произвольной выбранной точке с изменением температуры за время. На рис. 4, а, зависимость температуры от времени в 10 точке стержня. На рис. 4, б, для сравнения выведены три графика: желтый – зависимость температуры от времени в точке 10, синий – зависимость температуры от времени в точке 25, зеленый – зависимость температуры от времени в точке 40.
2. Применение метода конечных разностей для решения двумерного уравнения теплопроводности.
Представленные на рис. 5, а и б, распределения температуры показывают тепловую карту пластины после нагрева в течение 100 с в диапазоне от 23 до 24 °C. Получены следующие результаты расчета: L = 0,1 м, H = 0,1 м, λ = 46 Вт/(м⋅oC), ρ = 7800 кг/м3, с = 460 Дж/(кг⋅oC).
С целью решения данной двумерной задачи были определены начальные условия, а именно длина и высота пластины, имеющие размеры L = H = 5, а также адиабатические горизонтальные границы, поддерживающие постоянные температуры Th и Tc на вертикальных границах, при условии наличия начальной температуры области решения T0, что визуализировано на рис. 3, б.
Сущность такого подхода состоит в дискретизации двумерного уравнения только в направлении Ох и получении одномерного уравнения и, как следствие, реализации повторной дискретизации уравнения только в направлении оси Oy. Таким образом, определение температурного поля на целом шаге по времени реализуется с помощью решения полученного одномерного уравнения, которое является устойчивым и имеет свойства суммарной аппроксимации. Вышеописанная схема в научной литературе встречается под названием локально одномерная схема А.А. Самарского [17, 18].
Заключение
В настоящей статье приведен обзор методов моделирования [18], потенциально применимых к моделированию тепловой карты криоконсервированных продуктов крови во время дефростации [19, 20]. Построены две модели уравнения теплопроводности для решения методом конечных разностей. Решение одномерного уравнения теплопроводности реализовано успешно, в результате реализации получены графики зависимости температуры от времени в выбранных точках. Что касается двумерного случая, то система уравнений решена с помощью формирования матрицы температур, однако при написании кода была допущена ошибка, не влияющая на процесс визуализации расчетов в Python. При разработке программы моделирования теплового поля градиентного типа, где на оси Ох задается длина, а на Oy высота, площадь графика – площадь пластинки, в свою очередь градиентом выступает показание температуры в каждой точке, использовалась библиотека matplotlib [21, 22]. Таким образом, в настоящей статье реализован расчет простых уравнений теплопроводности на базе Python с использованием метода конечных разностей.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-37-90037.


 science-review.ru
science-review.ru