Большая область современных исследований посвящена определению характеристик динамических нелинейных систем [1], так как они наиболее точно описывают многие реальные физические объекты. При этом всё более широко используется метод точечных отображений [2], при котором параметры системы вычисляются через равные промежутки времени. Этот метод позволяет простыми математическими приёмами смоделировать эволюцию сложных систем.
Благодаря рассмотренным особенностям, применение точечных отображений для исследования сложных динамических нелинейных систем является одним из наиболее перспективных приёмов. Он позволяет выявить зоны устойчивого и неустойчивого поведения систем [3], исследовать траектории изменения их параметров, многие вероятностные характеристики, причём даже для систем, описываемых уравнениями, не решаемыми точными математическими методами.
Родоначальником метода точечных отображений является знаменитый учёный А. Пуанкаре, а в трудах Д. Биркгофа данный метод стал основным инструментом для изучения поведения динамических систем, и с тех пор сфера его использования всё более расширяется.
Целью данной работы является создание программных средств для вычисления характеристик одного из видов точечных отображений – Дуффинга (иногда называемого отображением Холмса). Физически оно описывает процесс движения одномерной (точечной) частицы в потенциале (например, в электромагнитном поле). Оно помогает смоделировать такие разнообразные системы, как микромеханические структуры, наномеханические изоляторы, роторы, призмы в потоках жидкости, траектории движения крыльев насекомых, характеристики систем ультразвуковой резки и многие другие.
Программные коды для исследования систем Дуффинга написаны с использованием одного из наиболее популярных, наглядных и простых в освоении и применении языков Python и создаются для использования, доработки, изучения всеми желающими, поэтому размещаются для свободной загрузки на сайте авторов [4]. Данные разработки дополняют ранее произведённые исследования других типов динамических систем [5].
Материалы и методы исследования
Для многих динамических систем характерна особенность, что при некотором наборе начальных значений факторов и коэффициентов уравнений интерполяции они демонстрируют устойчивость, которая выражается в совпадении точек, получаемых в процессе итераций. Также есть области таких начальных значений факторов и коэффициентов уравнений, при которых система демонстрирует хаотичное поведение (то есть не возвращается в прежнее состояние). Однако обычно этот хаос также некоторым образом упорядочен (поэтому его часто называют детерминированным хаосом), то есть формируемые точки не уходят далеко от некоторых областей притяжения – аттракторов [6].
Рассмотрим теперь, что представляет собой исследуемое точечное отображение Дуффинга [7] и каким образом оно формируется. Данная динамическая система относится к классу двухмерных (то есть имеет два изменяемых фактора x и y), и её точечное отображение поэтому формирует некую фазовую картину (для получения которой необходимо разработать программу) на плоскости. Разрабатываемая программа должна показывать зависимость значений факторов х и у от номера итерации (условного времени, номера очередной формируемой на плоскости точки) и позволять исследовать некоторые вероятностные характеристики распределения параметров. Ставится также задача численного определения областей устойчивости и хаоса точечного распределения Дуффинга и отображения их в графическом виде.
Формулы для вычисления итераций отображения Дуффинга выглядят следующим образом:
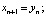
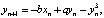
где а, b – постоянные множители, n – номер итерации вычислений.
Видим, что положение каждой последующей точки отображения зависит от предыдущей и т.д. Поэтому необходимо также задать координаты начальной точки.
Рассмотрим функции программы исследования отображения Дуффинга:
1. Импорт библиотек Tkinter и PIL – для формирования интерфейса; Matplotlib [8], Seaborn [9] – для обработки и вывода результатов в графическом виде.
2. Создание пользовательского интер- фейса.
3. Создание функции, заполняющей массивы факторов х, у, а также номеров итерации n.
4. Написание функции, осуществляющей вывод в графическом виде фазовой траектории, формируемой точками с вычисляемыми при множестве итераций координатами (х, у).
5. Создание функции, формирующей зависимости координат х, у от номеров итерации n.
6. Вычисление и построение статистических распределений факторов x, y.
Интерфейс созданной программы представлен на рис. 1.
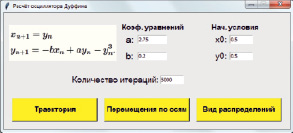
Рис. 1. Интерфейс программы для исследования точечного отображения Дуффинга
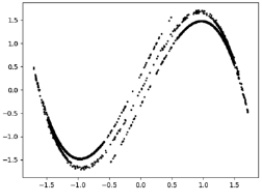
Рис. 2. Картина двухмерной фазовой траектории отображения Дуффинга, формируемая с параметрами программы по умолчанию
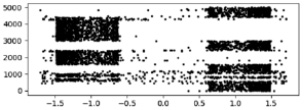
Рис. 3. Результаты вычисления перемещений по осям х, у в зависимости от номера итерации
Рисунок показывает вид программы с параметрами по умолчанию. Двухмерная фазовая траектория из точек, получаемая при нажатии на кнопку «Траектория», представлена на рис. 2.
Может показаться, что сформированная картина не является хаосом, так как видны линии, напоминающие участки синусоиды. На самом же деле каждая последующая итерация (точка) расположена достаточно далеко от предыдущей. Однако, как было отмечено выше, чем больше итераций отображается, тем больше заметно тяготение координат точек к определённым областям – аттракторам (при малом числе итераций это не так видно). Следовательно, реализованная функция «Траектория» позволяет исследователю проследить влияние различных параметров, задаваемых с помощью интерфейса программы, на картину, формируемую точками на плоскости. Если построить отображение для коэффициентов а и b, при которых поведение системы устойчиво, то на графике будут присутствовать лишь одна или несколько дискретных точек, причём для любого количества итераций количество дискретных точек будет одинаково. То есть система всегда возвращается к первоначальному состоянию.
Результаты выполнения следующей функции программы «Перемещения по осям» (реализованной с помощью модуля Seaborn для Python) приведены на рис. 3 (выводятся отдельно графики для х, у, но показан только один из них, так как они получаются одинаковыми).
Данный рисунок показывает, как координаты х, у зависят от номера итерации – виден «перескок» координат из одной области значений в другую. Также проявляется и тяготение координат к определённым областям. Данное распределение точек по диапазонам значений можно показать с помощью третьей функции программы «Вид распределений» (рис. 4).
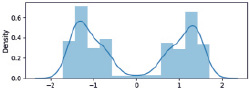
Рис. 4. Распределение значений х, у, формируемых при итерациях
В данном случае распределение по факторам х, у является одинаковым (симметричным), а наиболее вероятные значения факторов находятся вблизи областей с модами -1,25 и 1,25. То же самое видно и на рис. 2 и 3, но не столь явно. При других значениях задаваемых в интерфейсе программы, распределение и модальные значения могут быть другими, и программа позволяет их однозначно идентифицировать в каждом рассматриваемом случае.
Затем разрабатывалась программа для определения устойчивости отображения Дуффинга при изменении параметров a и b. Цвет точек графика показывает количество итераций, через которое картина возвращается к первоначальной. Если на каждой итерации система возвращается в одну и ту же точку с заданной точностью ε – цвет точки, соответствующий сочетанию a и b, устанавливается красным. Если возвращение происходит через одну итерацию (цикл возврата равен 1) – цвет оранжевый и т.д. до фиолетового цвета радуги, соответствующего циклу возврата 7. Если цикл больше 7, то считается, что система проявляет хаотичное поведение, и точка, соответствующая сочетанию a и b, окрашивается в чёрный цвет. Также возможны случаи, когда координаты x, y при заданном в настройках программы количестве итераций уходят в бесконечность – этот процесс называется слоением к бесконечности [10].
Определённое количество итераций до возврата в первоначальную точку называется циклом системы, а сама точка называется неподвижной точкой кратности n. В разрабатываемой программе кратность определяется только по восьми последним итерациям. Задав шаг движения по осям а и b и выводя разноцветные точки, соответствующие состоянию системы, получим диаграмму, называемую картой динамических режимов системы Дуффинга. Этот процесс осуществлён с помощью второй программы, код которой состоит из следующих блоков:
1. Импорт графической библиотеки Мatplotlib.
2. Задание пределов изменения коэффициентов точечного отображения Дуффинга a и b.
3. Присвоение значения переменной ε, указывающей допустимую разницу между сравниваемыми значениями координат системы Дуффинга на последней и предыдущих итерациях (вплоть до восьмой).
4. Основная часть программы, предназначенная для выявления описанной выше возможной цикличности итераций или хаотичного поведения системы и окрашивания точки, соответствующей каждому сочетанию коэффициентов а и b, в цвет, характеризующий степень устойчивости системы. Если факторы х или у уходят в бесконечность, то вычисление итерационного цикла прерывается и устанавливается белый цвет точки.
5. Осуществляется перебор значений коэффициентов а и b с заданным шагом.
6. Вывод в файл точечного графика, на котором цвет каждой точки, соответствующий разным координатам а и b и характеризующий степень устойчивости системы.
На рис. 5 приведены полученные с помощью второй программы карты динамических режимов системы Дуффинга при разных исходных данных.
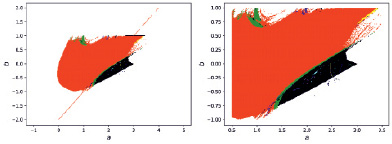
Рис. 5. Карты динамических режимом отображения Дуффинга
Результаты исследования и их обсуждение
С помощью полученного рисунка наглядно видны зоны устойчивого и хаотичного поведения системы Дуффинга. Можно выделить четыре основные области:
1. Чёрная зона в центре, в котором эволюция системы хаотична. Аргументы, для которых выше было получено хаотическое отображение, лежат на границе этой области, но при этом существует много других сочетаний а и b, при которых система проявляет хаотичное поведение. Исследование характеристик системы при этом возможно с помощью первой разработанной программы.
2. В центре карты динамических режимов располагается довольно чётко очерченная область устойчивого поведения системы с кратностью возврата 1 (красного цвета), хотя и за её пределами есть отдельные точки, где система столь же устойчива.
3. Зоны хаоса и полной устойчивости разделяет зелёная «линия», с кратностью возврата 4, которую можно условно назвать «областью колебаний».
4. Описанные зоны окружены областью стремления факторов к бесконечности. Это объясняется тем, что в итерационные уравнения входит степенной член.
По рис. 5 можно также сделать вывод, что параметры ε и t в исследуемых пределах почти не влияют на получаемую картину.
Методики исследования точечного отображения Дуффинга, описанные в данной статье, можно с успехом использовать также для исследования прочих видов точечных отображений, однако это потребует модификации кодов разработанных программ. Такая осознанная модификация позволит учёным глубже понять смысл и возможности применения одного из перспективнейших методов исследования – с использованием точечных отображений.
Заключение
Любой тип известных на данный момент точечных отображений позволяет описывать определённые классы реальных физических явлений, причём в данном исследовании показано, насколько наглядным является такой метод. Он является примером использования современных компьютерных математических алгоритмов для моделирования сложных физических систем (в данном случае динамических нелинейных). В описываемом исследовании разработаны две компьютерные программы, обладающие достаточно широкими возможностями, в том числе для визуального отображения результатов. Показано преимущество языка Python, обладающего всем необходимым набором модулей для организации обозначенных в целях статьи методах исследования.
При проведении исследований с помощью разработанной программы, строящей карту динамических режимов, установлен новый факт. Принято полагать, что хаотическое поведение системы Дуффинга наблюдается при следующих значениях коэффициентов отображения: а = 2,75 и b = 0,2. Однако, как показывают описанные исследования, существует достаточно обширная область значений, при которых наблюдается хаос.
Описанная методика должна помочь при совершенствовании современных методов исследования сложных систем с помощью доступных программных методов.


 science-review.ru
science-review.ru