science-review.ru
Конденсаторы являются одним из неотъемлемых элементов схем электроники. Основным параметром конденсаторов является электрическая ёмкость, величина которой зависит от его конфигурации: площади пластин, расстояния между пластинами и диэлектрической проницаемости среды, заполняющей внутреннюю полость конденсатора [1, 2]. Расчет простой модели плоского конденсатора с однородными параметрами и однородным заполнением диэлектриком проводится по хорошо известным соотношениям [3]. Более сложные конфигурации исследуются численно [4, 5]. Вместе с тем на практике однородность структуры может быть сравнительно хорошо обеспечена только в схемах макроскопических устройств. Поэтому при разработке устройств микроэлектроники и тем более устройств наноэлектроники неоднородность параметров в конструкции конденсатора представляет также самостоятельный интерес из-за возникающих дополнительных возможностей в управлении параметрами конденсатора. Кроме того, часто любой элемент схемы обладает емкостью, которая рассматривается как паразитная, расчет которой необходим для разработки рекомендаций по методам снижения паразитной емкости конструктивных элементов различных схем электроники. Использование технологии изготовления планарных элементов интегральных микросхем породило фундаментальную проблему развития аналитических методов расчета параметров интегральных схем различных частотных диапазонов. В общем случае используются численные методы [5]. Возможности расчета емкостей неоднородных структур рассматривались в [6]. В данной работе проведено обобщение формул для расчета емкости конденсаторов с различными неоднородностями конструкции (толщины слоя между пластинами конденсатора и неоднородности параметров диэлектрического заполнения полости конденсатора). Для большого числа функциональных зависимостей конфигураций d(x) и ε(x) получены аналитические соотношения для расчета ёмкости.
Цель исследования – вывод аналитических соотношений для расчета емкости неплоского конденсатора, формируемого конфигурацией двух проводников произвольной конфигурации и в общем случае с неоднородным заполнением диэлектриком.
Материалы и методы исследования
Для расчета емкости (рис. 1, a) используется формула для плоского элемента емкости площадью dS, для которого можно считать заполнение однородным с постоянной толщиной в области элемента dS:
.
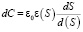В случае «квазиплоского» конденсатора расчет емкости конденсатора может быть проведен путем расчета выражения
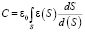(1)
где в области площади dS конденсатор может считаться плоским с расстоянием между пластинами d(S) и диэлектрической проницаемостью ε(S), зависящими от положения точки на поверхности S.
В частности, в декартовой системе координат формула для расчета емкости (рис. 1, a) принимает вид
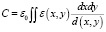(2)
В цилиндрической системе, которой ось 0z перпендикулярна плоскости токопроводящих полосок
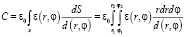.(3)
Результаты исследования и их обсуждение
Рассмотрим некоторые простейшие конфигурации, для которых можно получить аналитическое решение, представляющие практический интерес.
1. В частном случае для круглой обкладки полоскового конденсатора (в виде кольца или шайбы, рис. 1, b) с однородными параметрами диэлектрика и однородной толщиной из (3) имеем известное соотношение
,
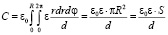где ε0 – диэлектрическая постоянная вакуума, ε – диэлектрическая проницаемость среды, заполняющей полость конденсатора (подложки), S – площадь пластин конденсатора, d – расстояние между пластинами [1–3].
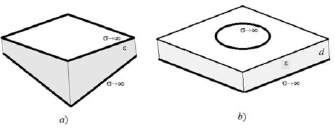
Рис. 1. Плоский конденсатор (a – с неоднородной толщиной, b – круглый)
Рассмотрим тонкую полоску токопроводящего элемента в виде кольца шириной r = r1 – r2, нанесенного на слой металлизированного с другой поверхности диэлектрика. Толщина подложки диэлектрика d.
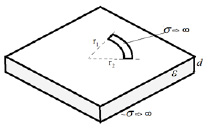
Рис. 2. Плоский конденсатор в виде сегмента кольца
Если неоднородность диэлектрической проницаемости описывается функцией ε(x) = εm / x , то емкость определяется формулой:
.
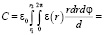
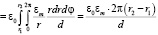Аналитические соотношения могут быть получены и для других функций распределения диэлектрической проницаемости.
Емкость части кольца с углом сектора, например φ = π / 4 и полоской проводника радиусами: внешним r2 и внутренним r1 с однородной подложкой диэлектрика (рис. 2) равна
.
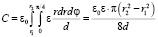2. Для описания зависимости ёмкости конденсатора от изменения расстояния между пластинами d необходимо используем общее выражение (1). Рассмотрим конденсатор с прямоугольными пластинами, у которого вдоль осей 0x и 0y периодически меняется расстояние между пластинами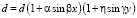 
.
Тогда емкость может быть найдена из выражения (2):
.
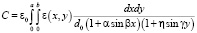В частном случае однородного диэлектрика имеем соотношение
3. Для случая проводящей сферы радиусом R, расположенной на расстоянии d0 от токопроводящей поверхности, расстояние между токопроводящими поверхностями при удалении от центра меняется по закону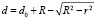 
(рис. 3, a).
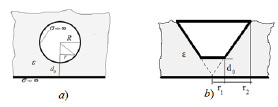
Рис. 3. Конденсатор со сферической (a) и конической (b) обкладками
Тогда из (3)
.
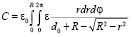Или, вводя обозначение x = r / R,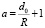 
, имеем
.
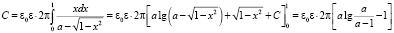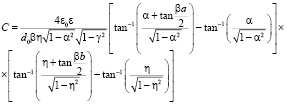
Таким образом,
.
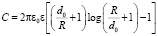4. Для случая конусообразной обкладки пластины конденсатора (рис. 3, b) с расстоянием между обкладками, меняющимся по закону d(r) = d0 + αr емкость определяется соотношением
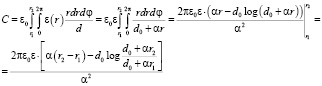
В частности, при r1 = 0
,
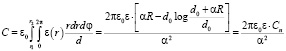где R – радиус конуса.
На рис. 4 показана зависимость нормированной емкости от величины конусности αr при различных d0.
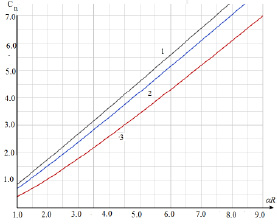
Рис. 4 . Зависимость емкости параметра конусообразности (1 – d0 = 0.5, 2 – d0 = 1, 3 – d0 = 2)
5. Если расстояние между обкладками пластин конденсатора меняется по закону d(r) = d0 + βr2, емкость определяется соотношением
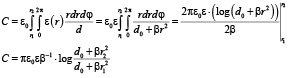
На рис. 5 показана зависимость нормированной емкости от коэффициента нелинейности функции расстояния между обкладками конденсатора.
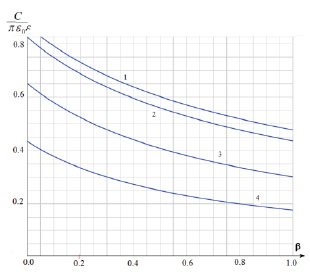
Рис. 5. Зависимость емкости от конструктивного параметра β (1 – r1 / r2 = 0, 2 – r1 / r2 = 0.05, 3 – r1 / r2 = 0.25, 4 – r1 / r2 = 0.5)
Таким образом, видно, что неоднородности конструкций конденсаторов приводят к изменению емкости в больших пределах и могут эффективно использоваться для управления параметрами конденсаторов.
Заключение
Получены аналитические решения задачи расчета емкости планарных конденсаторов на интегральных схемах с неоднородным распределением расстояния между пластинами и с неоднородным распределением диэлектрической проницаемости. Установлено, что неоднородности в структуре конденсатора могут быть использованы для управления параметрами конденсатора.