Теория графов занимается изучением специальных структур – абстрактного представления систем любой природы, объекты которых имеют попарные связи [1]. Граф является совокупностью двух математических множеств – множества исследуемых объектов, называемого множеством узлов (вершин), и множества связей вершин, называемого множеством рёбер [2]. Таким образом, получается, что каждое ребро является зависимым от положения вершин, а также часто может характеризоваться направлением от одной вершины к другой. В теории графов (называемой ещё теорией сетей) организация таких связей позволяет достичь параллелизации процесса прохождения информации, ускоряя таким образом данный процесс [3]. Применение теории графов позволяет во многих случаях уменьшить загрузку узлов (а конкретно – снизить использование памяти и нагрузки процессоров в компьютерных сетях) [4]. В случае сильно разветвлённых сетей теория графов позволяет произвольно изменять прохождение информационных потоков через разные группы узлов, добиваясь наибольшей пропускной способности, предотвращения зашумления информации и достигая при этом наименьшей загрузки кромок.
Теория графов применяется во многих науках, но наибольшее употребление нашла в информатике и в разработке сетевых технологий. В настоящее время существует множество специальных программ и функций, позволяющих производить автоматизированную визуализацию схем, строящихся в теории графов [5]. Наиболее удобным для применения представляется современный модуль для среды программирования Python, позволяющий автоматически строить графы, который называется DeepGraph [6]. Он был разработан с использованием модуля научных вычислений Pandas [7] и даёт возможность разработчику реализовать вывод на схему графа как узлов сети (DataFrames), так и изображения связывающих их кромок. Также имеется возможность организации так называемых многослойных сетей (в которых, например, рассматривается изменение положения узлов с течением времени или трёхмерная архитектура сетей) [8].
Модуль DeepGraph является достаточно «продвинутым», но при этом и специфичным средством изображения и исследования особенностей организации графов. Хотя он не может создать конкуренцию таким «тяжёлым» средствам разработки локальных сетей для Python, наиболее известным из которых является NetworkX [9], его задачей является расширение функциональности данной среды программирования путём применения наиболее наглядных (но сочетающих при этом классические приёмы) визуальных средств. При этом достоинством DeepGraph является простота его освоения и интуитивного понимания параметров используемых в нём функций.
Целью данной работы является исследование возможностей визуализации различного типа графических сетей с помощью библиотеки DeepGraph и разработка на их основе методик работы с функциями модуля (создания узлов сетей разного типа, а также соединения их кромками).
Материалы и методы исследования
Первая методика визуализации узлов сети не требует даже использования модуля DeepGraph, достаточными являются функции библиотеки Pandas языка Python. Методика включает в себя последовательное применение следующих действий:
1) импортирование подбиблиотеки Pyplot графической библиотеки Matplotlib;
2) подключение модуля расширения Numpy [10] для добавления поддержки работы с массивами данных и библиотеки научных функций Pandas;
3) настройка параметров построчного вывода данных из подгружаемых баз данных модуля Pandas;
4) выполнение команды Pandas для чтения файла;
5) определение размеров изображаемой сетки графа с помощью модуля Matplotlib;
6) применение команды Scatter [11] библиотеки Matplotlib для изображения узлов графа, создаваемого по загруженной базе данных;
7) запись сетки графа на жёсткий диск в виде графического файла (например, имеющего формат jpg или png).
Используем данную методику для построения простой сетки графов без рёбер, соединяющих узлы. Как пример базы данных используем файл «flying_balls.csv» (с разделителями данных – запятыми), взятый из архива [6], структурированный следующим образом (приведён заголовок с названиями данных и первые несколько содержащих их строк; всего же файл содержит 1169 строк):
,time,x,y,ball_id
0,0,1692.0,0.0,0
1,0,8681.0,0.0,1
2,0,490.0,0.0,2
3,0,7439.0,0.0,3
Каждая строка приведённого файла данных содержит пять значений: первое означает номер строки, второе – номер графического слоя (означающий, например, время), третье – координату х, четвёртое – координату у, пятое – номер графа в текущем слое.
Данный граф является многослойным (с помощью слоёв можно имитировать поведение точек графа во времени), но при его изображении в файл выводятся только узлы (без рёбер). На рис. 1 изображена результирующая графическая сеть, построенная по базе данных «flying_balls.csv» со следующими настройками относительного размера выводимых фигур: ширина 6, высота 4. В результате размер всего изображения, определяемый конфигурацией элементов базы данных, получился равным 10000х500.
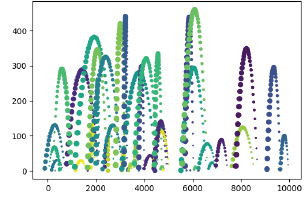
Рис. 1. Изображение многослойного графа, состоящего только из узлов
В приведённом примере команда построения точечного графика Scatter модуля Matplotlib для отображения времени протекания процесса преобразования узлов использует разный размер точек для разных моментов времени (с течением времени размер точки увеличивается). При этом для разных узлов графа используются разные цвета точек. Получающаяся таким образом команда построения узлов многослойного (мультивременного) графа выглядит следующим образом:
Scatter(v.x, v.y, s=v.time, c=v.ball_id),
где x означает координату х;
y – координату y;
s (size) – размер узловой точки (в зависимости от времени time);
c (color) – цвет точки (в зависимости от номера узловой точки).
Все представленные средства графического отображения различных характеристик графа делают получающееся изображение наглядным даже при его двухмерном представлении, как в данном случае.
Наряду с представленной методикой отображения баз данных в виде графов только с узлами, была разработана также и другая, более сложная, методика изображения сетевых графов ещё и с рёбрами. В данном случае для создания рёбер в программе становится необходимым использование специального модуля DeepGraph, включающего в себя ряд дополнительных функций. Также в программе необходимо сформировать четыре функции, определяющие координаты х и у начала и окончания каждого ребра. После этого заполняется массив координат рёбер (с использованием возможностей ещё одного дополнительного модуля Numpy), и полученные рёбра добавляются на изображение графа с применением команд графического модуля Matplotlib.Pyplot [12].
Также используются и описанные выше технологии, применяемые для создания графа, имеющего только узловые точки.
На рис. 2 изображён граф, полученный из файла данных «flying_balls.csv», с применением второй методики рисования сетевого графа, в котором узловые точки соединяются рёбрами в порядке увеличения номеров слоёв (по мере прохождения времени). Относительный размер и «скорость» уменьшения размера точки при этом взяты такими же, как и в первом примере (6 и 4 соответственно). Поэтому размер изображения получился, как и в первом случае (10000х500).
Результаты исследования и их обсуждение
Исходя из рис. 2 можно сделать вывод, что изображение сетевого графа, имеющее в своём составе соединяющие узлы рёбра, является более наглядным (при сравнении с рис. 1 без рёбер). В данном случае явственно видны пути смещения узлов при их временном развитии, полученные путём соединения найденных с помощью второй разработанной методики с использованием модуля DeepGraph координат начал и окончаний узлов. Так же как и рис. 1, данный граф является многослойным, и в некоторых областях рис. 2 это заметно.
Ещё более наглядным является трёхмерное изображение графа, которое можно вывести в графический файл при использовании функции Plot_3d библиотеки DeepGraph вместо использованной во втором методе функции Plot_2d.
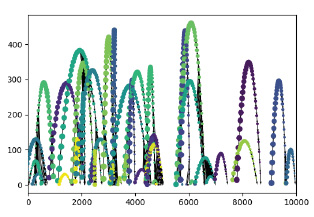
Рис. 2. Созданное из базы данных изображение сетевого графа, имеющего как узлы, так и рёбра
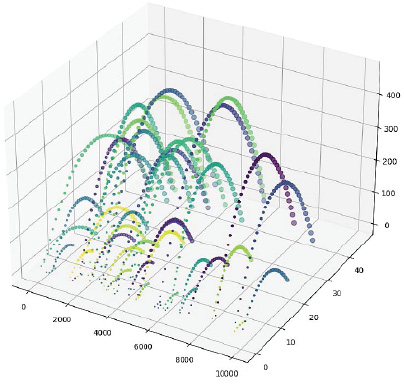
Рис. 3. Объёмное изображение сетевого графа
В качестве третьей координаты объёмного графика целесообразнее всего использовать графу базы данных «time» (время). Получаемая в этом случае картина для той же базы данных представлена на рис. 3.
В данном случае изменение положения узлов графа видно наиболее отчётливо, поэтому именно такой вид изображения рекомендуется использовать при демонстрации динамически изменяющихся сетевых графов.
Заключение
Таким образом, цели и задачи представленной работы полностью выполнены – разработаны действующие для любых баз данных три методики их визуализации в виде многослойных графов, как с использованием рёбер (и, соответственно, модуля DeepGraph), так и без использования рёбер, на которых присутствуют лишь узлы графа (в этом случае применение модуля DeepGraph не требуется), двухмерные и трёхмерные. Показаны примеры построения графов с помощью всех разработанных методик, которые можно без существенной модификации (исключая список исходных данных) применять также для визуализации любых подобных баз данных. Результаты выполнения программных кодов являются достаточно наглядными и рекомендуются для применения при любых видах исследований, использующих теорию графов (т.е. описанная работа является прикладной, направленной на практическое использование). Среди многочисленных работ авторов, посвящённых применению языка Python для математических вычислений, данное исследование раскрывает ещё одну область использования данного универсального языка программирования.
По результатам визуализации графов можно сделать определённые выводы: например, в данном случае становится понятным, что с течением времени положение каждого узла смещается по параболе своей, определённой, формы и что перемещение отдельных узлов является независимым.
Также можно сделать вывод и об удобстве и простоте применения именно библиотеки функций DeepGraph для обработки несложных баз данных. Также лёгкость понимания лежащих в основе разработанных методик алгоритмов позволяет рекомендовать использование языка программирования Python совместно с описанными библиотеками функций (главной из которых, конечно же, является модуль DeepGraph) для решения задач, связанных с визуализацией поведения сетевых графов, благодаря следующим доказанным достоинствам данного подхода:
1) высокая скорость вычислений и построения графических моделей;
2) понятность алгоритмов и кодов программ;
3) наглядность и многообразие форм визуализации результатов обработки баз данных;
4) использование только свободно распространяемых и доступных всем программных продуктов;
5) достижение понимания исследователем всех рассматриваемых процессов: от формулирования до визуализации решения задач, что является особенно важным для впервые изучающих рассматриваемые методы.
Методики и блоки программ на языке Python, разработанные в данной работе, можно использовать также внутри любых других программных продуктов.


 science-review.ru
science-review.ru