Предварительная обработка данных в машинном обучении – это важный шаг, который помогает повысить качество данных. Предобработка данных в машинном обучении относится к технике подготовки необработанных данных с целью сделать их пригодными для построения и обучения моделей машинного обучения. Иными словами, это метод интеллектуального анализа данных, который преобразует необработанные данные в понятный и читаемый формат.
Предварительная обработка данных является одним из основных этапов, от качества выполнения которого зависит получение качественных результатов процесса анализа данных. Без подготовки данных не обходится ни один нейросетевой метод. Как правило, при описании различных нейроархитектур предполагается, что данные для обучения уже представлены в том виде, в котором требует нейросеть, однако на практике дела обстоят совсем иначе, именно этап предобработки данных может занимать большую часть времени, отведенного на проект в целом. Результат обучения нейросети также может зависеть от того, в каком виде представлена информация для ее обучения. Таким образом, предварительная обработка данных позволяет повысить качество как интеллектуального анализа данных, так и самих данных.
Цель исследования – рассмотрение этапов предварительной обработки данных и основ разработки признаков, а также обзор конструирования категориальных признаков.
Материалы и методы исследования
При создании модели машинного обучения предварительная обработка данных служит первым шагом. Как правило, реальные данные являются неполными, непоследовательными, могут содержать ошибки или выбросы, а также в них могут отсутствовать конкретные значения или атрибуты. Именно здесь используется предобработка данных: она помогает очищать, форматировать и упорядочивать необработанные данные, тем самым делая их готовыми к работе с моделями машинного обучения.
Предобработка данных состоит из пяти этапов:
− очистка данных, которая направлена на повышение качества данных за счет присваивания пропущенных значений и удаления выбросов;
− сокращение объема данных, которое уменьшает объем данных и, следовательно, снижает связанные с ними вычислительные мощности;
− масштабирование данных – направлено на преобразование исходных данных в аналогичные диапазоны для прогнозного моделирования;
− преобразование, целью которого является организация исходных данных в подходящие форматы для различных алгоритмов интеллектуального анализа данных;
− разделение, которое делит весь набор данных на различные подмножества для более глубокого анализа.
Существует два общих способа обработки отсутствующих значений при построении оперативных данных. Первый – просто отбросить выборки данных с пропущенными значениями, так как большинство алгоритмов получения данных не могут обрабатывать данные с пропущенными значениями. Такой метод применим только тогда, когда доля отсутствующих значений незначительна. Второй – применение методов интерполяции пропущенных значений для замены пропущенных данных значениями, полученными в результате расчетов.
Как показано на рисунке 1, распространенные методы интерполяции отсутствующих значений можно разделить на две группы, т.е. одномерные и многомерные методы.
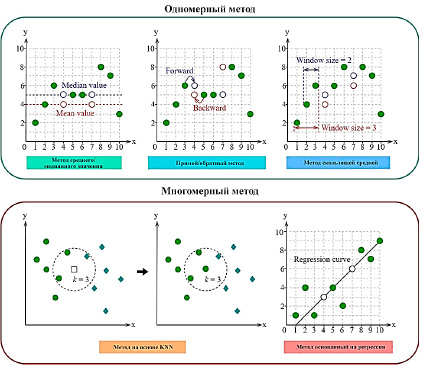
Рис. 1. Методы интерполяции пропущенных значений для построения данных
К первым относятся средняя интерполяция, прямая или обратная интерполяция и методы скользящего среднего. В этом случае недостающие значения выводятся на основе характеристик данных только одной переменной и поэтому называются одномерными методами. Метод интерполяции среднего или медианы заменяет недостающие значения средним или медианой этой переменной. Прямой или обратный метод просто заменяет отсутствующее значение предыдущим или следующим измерением данных. Эти два метода просты в реализации, но не учитывают временные корреляции на временных этапах и могут не сделать правильную замену данных [1].
В основном используются два метода обнаружения выбросов – статистические методы и методы, основанные на кластеризации.
Сокращение данных обычно проводится в двух направлениях, т.е. по строкам для сокращения выборки данных и по столбцам для сокращения переменных данных. Для сокращения данных по строкам могут применяться различные методы выборки данных, такие как случайная и стратифицированная выборка.
Существуют три основных метода сокращения переменных данных по столбцам. Первый заключается в использовании знаний о домене для прямого отбора интересующих переменных. Второй – использование статистических методов отбора признаков для выбора важных переменных для дальнейшего анализа. Третий – использование методов извлечения признаков для построения полезных признаков для анализа данных.
Масштабирование данных часто необходимо для обеспечения достоверности прогностического моделирования, особенно когда входные переменные имеют различные масштабы. Нормализация max-min (т.е., x′=x-xmin/xmax-xmin) и стандартизация z-score (т.е., x′=x-μ/σ) – два наиболее широко используемых метода, где min(x) и max(x) означают минимум и максимум переменной x, значения переменной μ – среднее значение, а σ – стандартное отклонение.
Метод нормализации max-min чувствителен к выбросам данных, поскольку их присутствие может резко изменить диапазон данных. В отличие от него метод стандартизации z-score менее подвержен влиянию выбросов. Он обычно используется для реформирования переменной, чтобы она была нормально распределена со средним значением, равным нулю, и стандартным отклонением, равным единице. Теоретически, нормализация по z-score работает лучше всего, когда данные нормально распределены. Нормализация по методу max-min рекомендуется, когда эксплуатационные данные не соответствуют нормальному распределению и не содержат явных выбросов. Другой тип метода масштабирования данных может изменять структуры данных. Например, исходные данные могут быть отображены в новое пространство с помощью определенных математических функций, таких как логарифмическая, сигмоидальная функции или арктангенс. Такие методы часто используются для минимизации дифференциалов в переменных данных [2].
Преобразование данных в основном применяется для преобразования числовых данных в категориальные для обеспечения совместимости с алгоритмами интеллектуального анализа данных. Методы равной ширины и равной частоты широко используются благодаря своей простоте. Количество интервалов обычно предопределяется пользователем на основе знаний о предметной области. По сравнению с методом равной ширины метод равной частоты менее чувствителен к выбросам [3].
Преобразование данных также может применяться для преобразования категориальных переменных в числовые для облегчения разработки моделей прогнозирования. Для этой цели широко используется метод однократного кодирования, при котором для категориальной переменной с L уровнями создается матрица из L – 1 столбцов [4]. Все признаки могут быть следующих видов:
− бинарные, которые принимают два значения (да/нет, 0/1, true/false);
− номинальные, которые имеют конечное количество уровней. Также они могут быть упорядоченными и неупорядоченными;
− количественные значения в диапазоне от –∞ до +∞.
Признак – это переменная, которая описывает отдельную характеристику объекта. В табличном представлении выборки признаки – это столбцы таблицы, а объекты – строки. Входные, независимые переменные для модели машинного обучения называются предикторами, а выходные, зависимые – целевыми признаками.
Признаки могут извлекаться из данных любого типа, в том числе из текста, изображений и геоданных. При обработке текстовой информации сначала выполняется ее токенизация, а затем лемматизация и цифровизация – перевод слов в числовые вектора. В случае изображений часто анализируется не только содержание картинки как набора пикселей различного цвета, но и метаданные графического файла: дата съемки, разрешение, модель камеры и т.д. Географические данные чаще всего представлены в виде адресов или пар [5].
Разработка признаков – очень важный аспект машинного обучения и науки о данных, и его нельзя игнорировать. Основная цель разработки признаков – получить наилучшие результаты от алгоритмов. В науке о данных производительность модели зависит от предварительной обработки и обработки данных. Если модель построена без обработки данных, то точность будет составлять около 70%. Применив генерацию признаков к той же модели, производительность можно повысить на несколько десятков процентов. Проще говоря, благодаря генерации признаков улучшается производительность модели.
Выбор признаков – это не что иное, как выбор необходимых независимых признаков. Выбор важных независимых признаков, которые имеют большую связь с зависимым признаком, поможет построить хорошую модель. Существует несколько методов отбора признаков [6].
В случае одномерного массива статистические тесты могут использоваться для отбора независимых признаков, которые имеют наиболее сильную связь с зависимым признаком. Метод SelectKBest может быть использован с набором различных статистических тестов для выбора определенного количества признаков (рис. 2). Признак, имеющий наивысший балл, будет более связан с зависимым признаком, и эти признаки будут выбраны для модели.
Метод ExtraTreesClassifier помогает определить важность каждого независимого признака с зависимым признаком. Важность признака дает оценку для каждого признака данных: чем выше оценка, тем важнее или релевантнее признак текущей выходной переменной (рис. 3).
Тепловая карта – это графическое представление двумерных данных (рис. 4). Здесь каждое значение данных представлено в матрице. Необходимо построить парный график между всеми независимыми и зависимыми функциями, в итоге получится отношение между двумя признаками. Если отношение между независимой и зависимой функциями меньше 0,2, тогда эта независимая функция выбирается для построения модели.
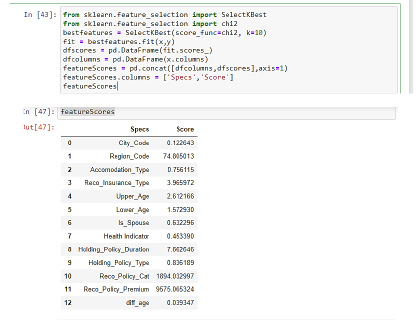
Рис. 2. Пример одномерного отбора
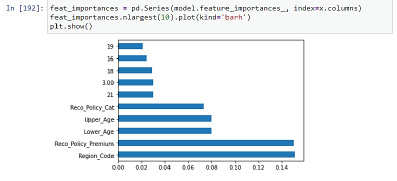
Рис. 3. Пример метода ExtraTreeClassifier
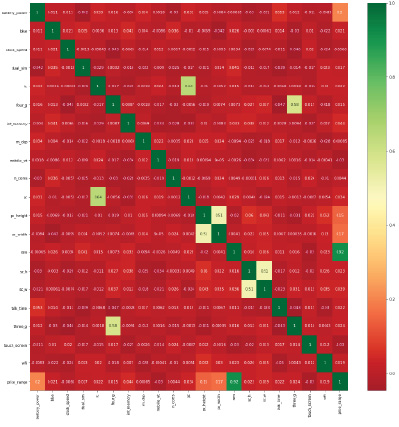
Рис. 4. Пример тепловой карты
Категориальные данные – это тип данных, который используется для группировки информации с похожими характеристиками, в то время как числовые данные – это тип данных, выражающих информацию в виде чисел. Примером категориальных данных может служить пол человека [7].
Большинство алгоритмов машинного обучения не могут работать с категориальными переменными, если их не преобразовать в числовые значения. Производительность многих алгоритмов даже зависит от того, как закодированы категориальные переменные.
Категориальные переменные можно разделить на две категории:
− номинальные, которые не имеют определенного порядка;
− порядковые, между значениями которых существует определенный порядок.
Заключение
Предобработка данных является важнейшим этапом построения моделей машинного обучения, она занимает большую часть времени, так как от подготовки данных зависит корректность будущей модели. В случае ошибки при первичном анализе возможны переобучение модели или утечка данных, которые могут нарушить корректность работы модели. Таким образом, предварительная обработка данных позволяет значительно повысить качество как самих данных, так и результата анализа.


 science-review.ru
science-review.ru