science-review.ru
Сохранение и даже приумножение временно свободного финансового ресурса экономических агентов (физических лиц, домохозяйств, предприятий, управляющих органов экономических территорий, организаций финансового сектора экономики и пр.) независимо от стадии общественного развития и состояния экономики является актуальной проблемой стратегического характера, решение которой позволяет сгладить негативные последствия действия объективного экономического закона убывания во времени стоимости финансового ресурса (столь же объективного, как закон трения в технической системе). При этом одним из способов решения указанной задачи является размещение свободных финансовых средств в инвестиционных фондах (ИФ) путем построения оптимальных (по заданным критериям) портфелей инвестиционных проектов различного характера – финансового и/или производственного. Задача построения оптимального инвестиционного портфеля по двум критериям – максимум рентабельности и минимум рисков – решена во второй половине ХХ в. Г. Марковицем [1] и Дж. Тобиным [2] в постановке, подразумевающей наличие информации об относительных доходностях и корреляционных связях проектов в портфеле. Значительная доля появившихся позже моделей и методов анализа оптимальных инвестиционных портфелей посвящены совершенствованию и разработке модификаций моделей Марковица–Тобина с точки зрения учета различных особенностей функционирования финансовых и нефинансовых активов на валютных и фондовых рынках и базируются, как правило, на концепции имитационного моделирования и использования регрессионно-статистических (в том числе стохастических) подходов, обзор которых здесь не проводится.
В работе [3] построена математическая модель инвестиционного фонда в форме многопараметрической задачи линейного программирования с критерием максимизации дисконтированной добавленной стоимости портфеля. В этой модели предполагается наличие интегрального инвестиционного ограничения на всю максимальную сумму инвестиционных средств портфеля, что часто не соответствует финансовой практике формирования инвестиционных портфелей. В связи с этим целями данного исследования являются учет данной содержательной особенности и внесение соответствующей модификации в указанную модель.
Материалы и методы исследования
Для осмысления и достижения указанной цели видится целесообразным проанализировать особенности модели [3], отличающие ее от моделей Г. Марковица и Дж. Тобина. В связи с введением группы искомых переменных модели, отвечающих за оптимальные объемы производимой продукции (товаров и/или услуг) в проектах портфеля, а также в связи с наличием ограничений на указанные переменные, имеющих содержательный смысл непревышения максимальных производственных мощностей, могут быть рассмотрены: 1) стоимость и производительность комплектов основных производственных активов (КПА) материального и нематериального характера, используемых для производства продукции n видов в каждом из n проектов портфеля (в соответствии с принципом чистых отраслей); 2) рыночная цена единицы и стоимостная оценка спроса как характеристики производимой продукции n видов, причем стоимостная оценка спроса соответствует оценке прогнозной доли рынка продукции. Через указанные в пунктах 1) и 2) характеристики могут быть определены относительные экономические эффективности δi (i = 1,…,n) КПА входящих в инвестиционный портфель проектов в виде отношения произведений рыночной цены единицы продукции и производительности КПА к их стоимости (для каждого из n КПА) и трактоваться как рентабельность (фондоотдача и пр.) производственных активов проекта или как относительная эффективность самих проектов. Следует отметить, что данный подход принципиально отличает модель в [3] от оригинальных моделей Марковица–Тобина и большинства исследующих их моделей, в которых предполагается априорное задание показателей относительной эффективности проектов портфеля без объяснения способа формирования этих показателей. При этом большинство показателей модели в [3] могут быть получены в результате маркетинговых исследований, а также из официальной бухгалтерской отчетности предприятий, с сайтов экономической статистики территорий (например, [4]), что значительно расширяет возможности формирования содержательной информационной базы при формировании и ранжировании относительных показателей эффективности проектов ИФ.
Достаточно критичным вопросом в моделях Г. Марковица и Дж. Тобина также является вопрос необходимости наличия информации о корреляционных связях проектов в виде ковариационной матрицы, получение которой часто невозможно из-за трудностей корректного определения взаимозависимости проектов портфеля, реализующихся в основном в различных экономических условиях, включая производственные особенности (например, для энергетических, биотехнологических, информационно-технологических, сельскохозяйственных и других проектов), на которые могут влиять трудносопоставимые друг с другом политические, социальные, региональные, экологические и тому подобные факторы. В связи с этим в качестве другого критерия эффективности, минимизирующего риски функционирования ИФ, целесообразно выбирать показатели, значения которых также могут быть «считаны» с глобального финансового рынка, а также с рынков производимой в проектах ИФ продукции, на основе содержательно единообразной информационной базы (горизонт планирования, ставки дисконтирования в каждом проекте, инвестиционные, производственные и финансовые ограничения и особенности производства продукции в проектах и т.п.).
Следует отметить еще одно преимущество модели [3] относительно модели Дж. Тобина, предполагающей обязательное включение в инвестиционный портфель особого, безрискового финансового актива (например, в виде облигаций центрального банка страны), изначально снижающего общую эффективность всего портфеля в пользу минимизации рисков его функционирования, выраженных в виде потенциальных финансовых потерь инвесторов фонда. Предложенная в [3] модель не требует поиска такого актива, то есть лишена указанного недостатка. Помимо изложенных, в модели [3] учитываются и другие особенности функционирования и рыночного окружения ИФ, отсутствующие в моделях Г. Марковица и Дж. Тобина. А именно, в указанной модели напрямую формализован учет интересов менеджмента инвестиционного фонда через параметр ежегодного вознаграждения за управление его активами. Кроме того, в ней математически формализован учет неодновременности включения проектов в портфель фонда и длительности операций по проектам путем применения взаимосвязанных дисконтирующих множителей как метода учета различных рисков, связанных, в частности, с инфляцией, требованиями заемщиков финансовых средств и т.п. Впрочем, с точки зрения условия неодновременности включения и различной длительности операций по проектам в портфеле переход к классическим моделям формализуется как простейший частный случай с одновременным включением всех проектов в портфель и их исключением из него.
Построим экономико-математическую модель инвестиционного фонда.
Предварительно введем следующие обозначения:
n – количество проектов в ИФ, k=1,…, n – номер проекта в ИФ;
xk – инвестиции в k-й проект портфеля, д.е.;
xn+k (k=1,…,n) – потенциальный стоимостной объем производства продукции в k-м проекте портфеля, д.е.;
x2n+l (l=1,…,L) – затраты менеджмента ИФ на избежание (устранение) l-го риска его функционирования, д.е.; L – количество рисков в деятельности ИФ,
Т – горизонт планирования деятельности ИФ, ед. времени;
r – ставка дисконтирования на горизонте планирования деятельности ИФ, %;
сk – стоимость КПА в k-м проекте;
Vk – производительность КПА в k-м проекте;
Pk – цена единица продукции, производимой в k-м проекте;
δk = PkVk / сk – эффективность (рентабельность, фондоотдача) k-го проекта, %;
tk – момент начала k-го проекта, ед. времени;
Tk – момент окончания k-го проекта, ед. времени;
qk – емкость рынка (стоимостная оценка спроса) продукции k-го проекта, д.е.;
Ik – максимальные объемы инвестиций в k-й проект портфеля, д.е.;
ak – минимальный объем инвестиций в k-й проект, д.е.;
rk – ставка дисконтирования для k-го проекта, %;
bl – максимальные издержки, которые несет менеджмент ИФ в случае реализации риска на l-ом рисковом направлении функционирования, д.е.;
cl – задаваемые экспертно коэффициенты, имеющие смысл оценочной значимости эффекта от осуществленных затрат на l-ом рисковом направлении функционирования, д.е.; l=1,…,L;
s – ежегодное вознаграждение менеджерам управляющей компании за управление активами; ИФ – доля от первоначальной стоимости инвестиций, %;
γ – экспертная оценка доли суммарных инвестиций, используемых менеджментом на страхование деятельности ИФ, %;
LMAX – максимальные затраты на избежание (устранение) всех выделенных рисков функционирования ИФ, д.е.
Результаты исследования и их обсуждение
Учитывая введенные обозначения, модель портфеля ИФ имеет следующий матричный вид:
A(4n+3)×(2n+L)X(2n+L)×1 ≤ B(4n+3)×1,
X(2n+L)×1 ≥ 0,
C1×(2n+L) X(2n+L)×1 → max,
где
A =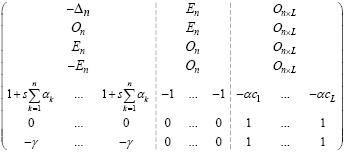 
,
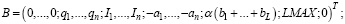
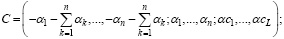
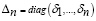– диагональная матрица с указанными элементами на диагонали;
Еn, Оn, Оn×L – единичная матрица и нулевая матрица размера n×n и нулевая матрица размера n×L соответственно;
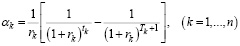– ставки дисконтирования каждого из n проектов портфеля с учетом разновременности моментов их начала и окончания;
α = Т / (1 + rэ ) – коэффициент дисконтирования на горизонте Т;
rэ = rT / (1 – (1 + r)-T) – 1 – эффективная ставка дисконтирования в предположении равномерности распределения суммарных затрат менеджмента на избежание (устранение) рисков функционирования ФПИ на горизонте Т.
Построенная модель является многопараметрической однокритериальной задачей линейного программирования с критерием максимизации дисконтированной добавленной стоимости портфеля, обобщающей модель работы [3] на случай инвестиционных ограничений для каждого из участвующих в портфеле проектов. Оптимизационность представленной модели позволяет автоматизированно выявлять экономический потенциал (максимальные финансовые возможности с точки зрения ключевого показателя эффективности – чистой добавленной стоимости) инвестиционного портфеля и принимать обоснованные решения о его формировании [5]. Кроме того, построенную модель несложно обобщить на многокритериальный случай, выделяя, например, отдельно критерий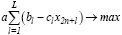 
, а затем переходя к эквивалентной однокритериальной задаче [6] путем рассмотрения выпуклой линейной свертки критериев. Заметим, что класс построенной модели (линейная задача оптимального управления) позволяет обосновать существование ее решения для всех допустимых значений параметров. Благодаря тому что существование тривиального решения в модели (путем параллельного переноса системы координат xk из точки аk в начало координат) легко проверяется, необходимо найти, например численно, нетривиальное решение, что и побуждает разрабатывать новые, основанные на такой модели системы автоматизированной обработки информации, которые, будучи ориентированными на конечного пользователя (в первую очередь, инвестиционного аналитика), рассматриваются как системы поддержки принятия управленческих решений по формированию портфеля реально функционирующих инвестиционных фондов, включающих значительное количество входящих в них инвестиционных проектов.
Важной, ранее не отмеченной особенностью построенной модели, как и модели в [3], является возникающая возможность ранжирования проектов портфеля с помощью автоматизированного комплекса «Карма», описанного в [5]. При этом, в отличие от предложенного в данной статье приема оценки относительных эффективностей δk проектов, оценка эффективности каждого проекта портфеля в отдельности может быть осуществлена автоматизированно, с учетом не только описанных характеристик КПА и продукции, но и с учетом инвестиционных (на объем инвестиций), производственных (на производственные мощности, трудо- и материалоемкость), финансовых (на объем собственных средств, кредитов и дотаций), рыночных (на объем спроса, ставки дисконтирования, горизонт планирования и т.п.) ограничений, что, очевидно, значительно повышает объективность ранжирования проектов портфеля за счет минимизации экспертных рисков их оценки. В связи с этим рассмотренная модификация модели инвестиционного портфеля, связанная с учетом инвестиционных ограничений на каждый из входящих в него проектов, имеет важный практический смысл.
Заключение
В работе рассмотрен подход, основанный на использовании таких инструментов управления инвестиционным портфелем активов, как двухступенчатая комбинация многокритериальной линейной модели оптимального управления и оптимизационной модели портфеля проектов. При этом взаимодействие проектов портфеля может рассматриваться в двух вариантах: 1) как взаимодействие набора полностью независимых (по характеристикам внутренней и внешней среды) проектов; 2) как взаимодействие набора проектов, связанных общими характеристиками, ограничениями и/или рисками инвестиционного, производственного и финансового характера. Это делает возможным применение указанного подхода на максимально широком спектре финансовых и производственно-финансовых систем микро-, мезо-, макроэкономического уровня. После определения показателей рентабельности проектов портфеля, с учетом описанных характеристик в них КПА и производимой продукции, а также ограничений их функционирования инвестиционного, производственного и финансового характера они могут быть использованы при ранжировании проектов ИФ в представленной здесь модели.
Благодаря используемому математическому классу задач (линейная модель оптимального управления с допустимым множеством в форме непустого компакта), нетривиальности и содержательной адекватности постановок, наличию эффективных алгоритмов численного анализа совокупность представленной математической модели и автоматизированного программного комплекса может рассматриваться как инструмент оперативной экспертной оценки экономической эффективности и принятия управленческих решений в банковской сфере, в ситуационных центрах социально-экономического анализа, а также как элемент цифрового социально-экономического двойника территории [7], на которой, например, функционирует конкретный инвестиционный фонд [8–10], и определять, в частности, финансовые возможности развития такой территории, как экономический объект.