В современном мире огромное множество однотипных объектов являются связанными между собой, образуя сетевые структуры [1]. Яркими примерами могут служить локальные и глобальные компьютерные и транспортные сети, социальные связи между людьми (сотрудничество учёных в разных организациях, городах и странах), финансовые связи между денежными потоками, взаимодействие предприятий (каждое из которых осуществляет свою стадию цикла проектирования и изготовления изделий), нейронные связи в организмах и т.д. [2]. Появляются и новые модели сетевых структур, в том числе созданные авторами данной статьи [3], позволяющие усовершенствовать методики исследований многих объектов и процессов. Как правило, сетевые структуры являются очень сложными по структуре и топологии (по способу взаимного соединения их компонентов) [4, 5].
Для упрощения разработки и анализа сетей они представляются в виде набора так называемых узловых точек (или узлов), которые соединяются с помощью связей, называемых рёбрами. Если информационный, энергетический или материальный поток может распространяться по ребру только в одном направлении, такое ребро называется направленным. Если все рёбра сети являются направленными, то вся сеть является направленным графом; если все связи могут осуществляться в двух направлениях, то это ненаправленный граф [6].
Граф является визуализацией сетевой структуры, и его топология может иметь совершенно разное строение. В общем случае (при отсутствии ярко выраженной закономерности) топология является смешанной, однако во многих случаях связи подчинены некой закономерности (называемой, например, звездой, шиной, кольцом, деревом, а также обозначаемой прочими терминами). Весьма сложной, а иногда неразрешимой задачей является построение графа, состоящего из десятков, сотен и тысяч узлов и рёбер, «вручную». В таких случаях необходимо прибегать к современным средствам автоматизации.
Цель данной работы состоит в создании методики построения сложных сетей и получения в результате этого процесса наглядного графического изображения их топологии, с использованием такого программного инструментария, как язык Python [7] совместно с рядом специальных библиотек функций. Также необходимо привести ряд примеров, наглядно демонстрирующих полученные результаты и позволяющих произвести начальный анализ топологии каждой изображённой сети.
Высокоуровневый язык Python выбран по причине того, что он позволяет создавать производительный и легко читаемый программный код, а также является свободно распространяемым продуктом. Для Python существует библиотека функций (модуль) NetworkX [8], предназначенная для обработки баз данных, представляющих из себя строки с обозначением соединяемых узлов и их основных параметров (атрибутов) и преобразования их в «сетевые» базы. Помимо этого, данный модуль, совместно с библиотекой Matplotlib [9], позволяет выводить созданную базу в виде графа, по-разному отображаемого на плоскости. Задачей является выбор наиболее наглядных способов отображения, позволяющих судить о топологии сети.
С помощью вышеупомянутых модулей, а также дополнительной библиотеки Numpy [10] можно автоматизировать анализ взаимозависимости характеристик топологии, выводимых в виде линейных графиков и гистограмм. Например, можно построить зависимость степеней узлов в сети (количества подсоединённых к ним рёбер) от их ранга (ранг обозначает узлы с одним и тем же количеством подключённых рёбер в порядке его возрастания).
Материалы и методы исследования
Рассмотрим методы визуализации топологии сетей, начиная с самых простых и заканчивая очень сложными.
Самой простой является программа визуализации и записи в графический файл топологии так называемой безмасштабной сети со случайным расположением узлов, состоящей всего из 6 строк кода на Python, однако позволяющей продемонстрировать базовые команды, необходимые для решения обозначенной цели исследования. Разберём код построчно:
1. import networkx as nx – импорт модуля работы с графами и сетями NetworkX.
2. import matplotlib.pyplot as plt – импорт модуля графического вывода Matplotlib.
3. D=nx.random_graphs.barabasi_albert_graph(20,1) – создание безмасштабной сети D со случайным расположением 20 узлов и с добавлением ребра к последующему создаваемому узлу.
4. nx.draw(D,pos=nx.random_layout(D),no de_size=25) – топологизация (присвоение случайных значений координат узлам с условным размером 25) созданной сети D.
5. plt.savefig(«net.png») – сохранение изображения сети в виде графического файла.
6. plt.show() – вывод изображения сети на экран.
Как видно из кода программы, она состоит из трёх блоков: импорт необходимых библиотек функций (модулей), использование модуля NetworkX для создания сети в виде базы данных координат её узлов, визуализация сети с использованием библиотеки Matplotlib. Результат работы программы приведён на рис. 1.
Так как координаты узлов создаются по случайному алгоритму, то при каждом запуске программы они будут располагаться в разных местах.
Теперь рассмотрим процесс визуализации сети, получаемой путём обработки базы данных, включающей в себя координаты узлов. В качестве такой базы данных взят файл, размещённый в [11] и представляющий из себя набор данных, собранный ещё в 1930-х гг. В нем содержится информация о социальных связях 18 женщин. Исходный файл данных содержит 278 строк, в каждой из которых указан начальный узел (номер одной женщины) и конечный узел (номер другой женщины), а также «вес» узлов, который во всех случаях равен 1 (это означает, что тип узлов одинаков). Таким образом, при визуализации связей каждая строка обозначает одно из рёбер графа (сети), которых соответственно насчитывается 278.
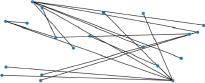
Рис. 1. Сеть (ненаправленный граф) со случайным расположением узлов
При создании сети из базы данных применяются дополнительные функции модуля NetworkX, например, Graph() для создания «пустого» графа, последовательно пополняемого данными о соединениях и «весах» узлов, которые затем сортируются на плоскости и соединяются рёбрами с целью создания топологии, определяемой алгоритмом этой сортировки.
Для создания топологии сети можно использовать множество методов. Рассмотрим один из них – spring_layout («пружинная компоновка»), при котором узлы позиционируются с помощью силового алгоритма Фрухтермана – Рейнгольда. Алгоритм рассматривает рёбра как пружины, притягивающие узлы как можно ближе друг к другу; узлы же при этом рассматриваются как отталкивающиеся из-за антигравитационной силы объекты. Моделирование продолжается до тех пор, пока действие сил на узлы не будет взаимно уравновешено.
Визуализация топологии сети, полученной из описанной выше базы данных с помощью метода spring_layout, представлена на рис. 2.
Несмотря на то, что анализируемая сеть отличается от предыдущей рассмотренной в данной статье гораздо большим количеством связей, выводимое визуальное изображение её топографии отличается компактностью. Также здесь все узлы снабжены маркерами, что также упрощает понимание топографии. Однако ясно, что даже при 18 узлах сложно проследить количество связей между ними, поэтому необходимо подобрать лучший для восприятия метод визуализации сети.
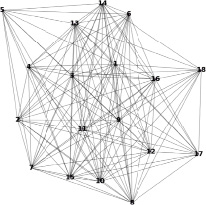
Рис. 2. Визуальное изображение топологии сети с 18 узлами, полученное с помощью пружинной компоновки
После детального изучения множества доступных в NetworkX методов отображения топологии, был выбран наиболее наглядный метод «круговой компоновки», использующий ещё один модуль Python, называемый Graphviz [12]. Этот метод был разработан Грэмом Уиллисом ещё в 1997 г. При его применении узлы размещаются на концентрических окружностях в зависимости от их расстояния от заданного корневого узла.
На рис. 3 показан результат применения круговой компоновки при построении сети по той же базе данных, что и рис. 2.
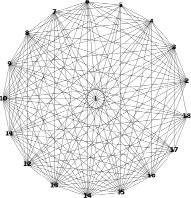
Рис. 3. Визуальное изображение топологии сети с 18 узлами, полученное с помощью круговой компоновки

Рис. 4. Анатомическая модель нейронных связей нематоды C. elegans
Круговая компоновка отличается от всех прочих высокой наглядностью взаимосвязей между узлами сети; кроме того её можно охарактеризовать как наиболее эстетичную в плане восприятия.
Очень интересно было рассмотреть, как будет выглядеть при выбранной компоновке очень сложная сеть, автоматически построенная по разработанному алгоритму. В качестве примера решено было использовать популярную в исследовательской среде нейросеть червя-нематоды C. elegans. Нейросеть данного многоклеточного организма хорошо изучена, и на данный момент известна информация обо всех его нейронах и о соединяющих их рёбрах.
Анатомическое расположение нейронов и связей между ними представлено на рис. 4.
База данных, содержащая сведения о нейросети нематоды (разработана в 2014 г.), доступна на сайте [13] и состоит из 2349 строк. Каждая строка содержит не только номера начальных и конечных связанных узлов (нейронов), которых насчитывается 306, но и количество щелевых контактов с соседними клетками в качестве «веса» начального узла (имеющих значение от 1 до 70).
Применение технологии круговой компоновки сети в данном случае даёт картину, показанную на рис. 5.
В дополнение к описанным выше средствам визуализации топологии столь сложной сети разными цветами радуги показаны веса узлов (третий параметр каждой строки обрабатываемого файла). Если вес равен единице, то узел обозначен тёмным (фиолетовым) цветом; чем больше вес узла, тем более яркий цвет ему соответствует. Например, максимальному весу 70 соответствует жёлтый цвет изображаемого узла. Номера узлов на рисунок не выводятся ввиду их очень большого количества.
Так как при большом количестве данных проследить связи между узлами становится проблематично на столь небольшой иллюстрации даже при использовании наилучшего метода визуализации, рекомендуется увеличивать масштаб изображения.

Рис. 5. Выбранный вариант наглядного визуального отображения топологии нейронной сети нематоды C. elegans
Заключение
Разработанные в ходе проведения работы методика и программа для автоматизации визуализации топологии сложных сетей обладают несомненными достоинствами по сравнению с методами, рассмотренными в начале статьи, так как они позволяют:
− наглядно показать узлы и связи между ними (тогда как исходный файл с численными значениями не обладает свойством какой-либо наглядности);
− с первого взгляда оценить степень сложности топологии, что является очень важным, например, при сравнении сетей разного типа и выбора из них наиболее приемлемой для проектировщика компоновки;
− узнать веса узлов (в качестве весов могут выступать разные параметры, например, в случае исследования компьютерных сетей цветом можно обозначить время пинга узлов).
Перечисленные достоинства приобретают особую важность при обучении будущих специалистов – проектировщиков сетей любого вида. Последний продемонстрированный пример показывает, что описанные средства можно применять не только в биологии и в нейросетевом программировании, но даже и при создании робота, имитирующего реакции живого организма (в случае реализации в нём созданной сети). Также некоторые примеры сфер использования методов визуализации топологии сетей приведены в начале статьи, однако данные сферы постоянно расширяются. По этой причине любому учёному (и не только) желательно освоить разобранные в статье технологии, основанные на самом современном и крайне популярном языке программирования Python с применением специальных библиотек функций.
Также всем заинтересовавшимся данной темой авторы статьи рекомендуют самостоятельно попробовать и выбрать для решения своих задач методы визуализации топологии сетей, так как для них может оказаться более наглядным другой вид компоновки (коих в рассмотренной библиотеке Graphviz для Python насчитывается множество [14], и они постоянно пополняются и совершенствуются).


 science-review.ru
science-review.ru