Если задуматься о том, как человек обучается, то, скорее всего, первой мыслью, приходящей в голову, будет идея, что этот процесс происходит при взаимодействии человека с окружающей средой. Контакты с окружающей средой, вне всяких сомнений, являются источником знаний как и о самом человеке, так и об окружающей его среде. Причем этот процесс длится на протяжении всей жизни человека. Взаимодействия с окружающей средой дают полную информацию о связи причин и следствий, о последовательности действий, которые нужно выполнить, чтобы добиться определенных целей. Именно обучение через взаимодействие является той основополагающей идеей, на которой базируются почти все теории обучения и интеллекта.
Изучение того, как сопоставить ситуации с действиями, чтобы получить максимальную выгоду, называется обучением с подкреплением. Обучающийся не знает заранее, какие действия необходимо предпринять, чтобы максимизировать вознаграждение. Поэтому он должен самостоятельно выяснить, какие действия нужно для этого сделать. К тому же, нужно учитывать, что выбор действия влияет не только на вознаграждение на данном этапе, но и на то, какую выгоду агент обучения может получить в дальнейшем. Эти две характеристики – поиск методом проб и ошибок и отложенное вознаграждение – являются двумя наиболее важными отличительными чертами обучения с подкреплением.
Главное при обучении с подкреплением – это зафиксировать основные аспекты реальной проблемы при взаимодействии обучающегося с окружающим миром для достижения своей цели. То есть агент обучения должен иметь цель, связанную с состоянием окружающей среды. Также учащийся должен иметь возможность ощущать среду и совершать действия, влияющие на нее.
Формулировка задачи обучения с подкреплением должна учитывать все три аспекта – ощущение, действие и цель – в их наиболее простых формах.
Агент обучения, чтобы получить наибольшее вознаграждение, как правило, отдаст предпочтение уже проверенным действиям, то есть тем, которые оказались эффективными для него в прошлом и дали ему лучшее вознаграждение. Но он не сможет найти такие действия, если бы ранее он не пробовал действия, которые раньше не выбирал. Из-за этого, одной из проблем, возникающей при обучении с подкреплением, является компромисс между изучением и применением. Получается, что обучающийся должен использовать то, что он уже испытал, чтобы получить вознаграждение, но он также должен изучить новое, чтобы сделать лучший выбор действий в будущем [1]. Агент обучения всегда должен пробовать различные действия, в дальнейшем отдавая предпочтения тем, которые оказались лучшими. Нельзя только использовать проверенные действия или только искать новые – в этом и состоит проблема.
В стохастической задаче каждое действие должно быть опробовано много раз, чтобы получить надежную оценку ожидаемого вознаграждения. Дилемма «изучение – применение» интенсивно изучается математиками на протяжении многих десятилетий, но до сих пор остается нерешенной.
Выделяют еще четыре основных элемента, помимо агента обучения и среды, входящих в систему обучения с подкреплением:
1. Стратегия.
2. Вознаграждение.
3. Ценность состояния.
4. Модель среды (необязательно).
Сопоставление состояний окружающей среды с действиями, которые должны быть выполнены в этих состояниях, называется стратегией. Проще говоря, именно стратегия определяет то, какой способ поведения выберет агент обучения в конкретный момент времени. В общем случае стратегия может быть случайной. В некоторых случаях она выражается функцией или таблицей, в более сложных вариантах – может даже включать какие-либо вычисления. Как правило, стратегии вполне достаточно для определения поведения агента обучения, является ядром агента.
Целью задачи обучения с подкреплением является вознаграждение – число, которое получает обучающийся на каждом шаге среды. Вознаграждение несет как положительный смысл, так и отрицательный для агента обучения, так как его основная цель – это максимизация общего вознаграждения, которое агент планирует получить в долгосрочной перспективе. Если провести аналогию с биологией, то вознаграждение можно сравнить с опытом боли или удовольствия. Если агент обучения получил низкое вознаграждение после действия, выбранного какой-либо стратегией, то это может являться основанием для смены стратегии в будущем. В общем случае вознаграждения могут быть случайными.
Ценность состояния – это общая сумма вознаграждения, которую агент обучения может получить в будущем, начиная с этого состояния. Как видно из определения, основным отличием ценности от вознаграждения является то, что она определяет то, что хорошо в дальнейшей перспективе. То есть конкретное состояние может давать небольшое моментальное вознаграждение, но за ним могут идти состояния, приносящие высокую выгоду, а следовательно, такое состояние будет иметь высокую ценность. Обратная ситуация так же может быть правдой. Если провести человеческую аналогию, то ценности соответствуют тому, насколько обучающийся доволен или недоволен тем, что его окружение находится в конкретном состоянии, тогда как вознаграждения в чем-то схожи с удовольствием, если значение выгоды высокое, или же с болью, если выгода низкая.
Цель оценки ценностей – получение большего вознаграждения. Без вознаграждения не может быть и ценностей, поэтому они в некотором роде первичны, а ценности – вторичны. Но, несмотря на это, именно ценности более интересны для принятия и оценки решений. Так как ценность рассматривает выгоду именно в долгосрочной перспективе, то выбор действий осуществляется именно на основе оценочных суждений, то есть таких действий, которые приводят к состояниям наивысшей ценности, а не наивысшего вознаграждения. К сожалению, определить вознаграждения намного легче, чем ценности. Ценности необходимо вычислять снова и снова из всей последовательности наблюдений, тогда вознаграждения в основном можно получить непосредственно из самой среды. Наиболее важный компонент практически всех алгоритмов обучения с подкреплением – это метод эффективной оценки значений функции ценностей.
И, наконец, последним и необязательным элементом является модель окружающей среды. С помощью модели можно делать выводы о том, как поведет себя среда, то есть задача модели – имитировать поведение самой окружающей среды. При помощи модели можно рассматривать возможные будущие ситуации и, в зависимости от этого, принимать решения о курсе действий. То есть модели используются для планирования: учитывая состояние и действие, она может предсказать то, в каком состоянии окажется окружающая среда, и соответствующее ему вознаграждение.
Таким образом, если для решения задач обучения с подкреплением используются модели и планирование, то методы решения называются методами, основанными на моделях. Противоположностью этих методов являются более простые методы, которые не используют модели, а учатся методом проб и ошибок.
Методы Монте-Карло – общее название группы численных методов. Они базируются на получении как можно большего количества реализаций случайного процесса, который формируется так, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи [2].
Методы Монте-Карло способны решить проблемы обучения с подкреплением, основываясь на усреднении результатов выборки. Чтобы обеспечить доступность четко определенных результатов, определим методы Монте-Карло только для эпизодических задач. Предполагается, что данные делятся на эпизоды, которые, так или иначе, будут завершены, независимо от того, какие действия выбраны. Только после того, как эпизод завершится, может произойти оценивание ценности или изменение стратегии. Таким образом, методы Монте-Карло могут быть инкрементными на уровне эпизодов.
Начнем с рассмотрения методов Монте-Карло для изучения функции значения состояния для заданной стратегии. Вспомним, что ценность состояния – это будущее накопленное вознаграждение, начиная с данного состояния. Таким образом, можно оценить выгоду, усреднив результаты полученной выгоды после пройденного состояния. Если число наблюдений будет расти, то, следовательно, количество значений выгоды также будет увеличиваться. А значит, среднее значение выгоды будет стремиться к ожидаемой величине. Данная идея лежит в основе методов Монте-Карло.
Введем следующие обозначения: пусть s – состояние, π – стратегия. Учитывая набор эпизодов, которые получились с помощью применения стратегии и прохождения через состояние, оценим ценность состояния s при стратегии π. Эта величина будет обозначаться следующим образом – vπ(s).
Посещением s называется каждое появление состояния s в эпизоде. Конечно, s может посетить один и тот же эпизод несколько раз. Назовем первое посещение в эпизоде первым посещением s. Метод Монте-Карло первого посещения оценивает vπ(s) как усреднение значения выгод, которые соответствуют первым посещениям s, тогда как метод Монте-Карло всех посещений оценивает величину как среднее значение после всех посещений s в эпизодах. Эти два метода Монте-Карло очень похожи, но имеют разные теоретические свойства.
В случае если число посещений стремится к бесконечности, то результат, который получается при использовании любого из вышеназванных методов, сходится к vπ(s).
В методе Монте-Карло оценка одного состояния никоим образом не базируется на оценке какого-либо другого состояния. Таким образом, эти оценки являются независимыми друг от друга. Этот факт является важной особенностью методов Монте-Карло.
Также интересной особенностью данного метода является то, что вычислительные затраты на оценку значения одного состояния не зависят от количества состояний. То есть можно создать большую выборку только нужных для работы эпизодов, не обращая внимания на остальные. И считать среднее значение выгоды только для этой выборки. Такая особенность делает методы Монте-Карло очень полезными, если необходимо оценить ценность только одного или некоторого подмножества состояний.
Если модель присутствует, то для определения стратегий достаточно ценностей состояния. Нужно просто сделать шаг и выбрать такое действие, которое приведет к наилучшему вознаграждению. Но если модель отсутствует, то таких данных будет недостаточно. И в таком случае лучше оценивать значения пар состояние – действие. Чтобы значения были полезны при выборе стратегии, нужно явно оценивать ценность каждого действия.
Таким образом, одной из основных целей для применения методов Монте-Карло является оценка q* . Чтобы достичь этого, сначала рассмотрим задачу оценки стратегии.
Задача оценки стратегии на основе значений действий состоит в том, чтобы оценить qπ(s,a) – ожидаемую выгоду при начале в состоянии s, выполнении действия a и последующем следовании стратегии π. Метод Монте-Карло для этого случая такой же, как и для рассмотренного ранее случая для значений состояния, за исключением того, что теперь оценивается пара состояние – действие, а не состояния. Метод Монте-Карло всех посещений оценивает ценность пары состояние – действие как среднее значение выгоды, полученной после всех посещений. Метод Монте-Карло первого посещения усредняет значения выгод после первого посещения в каждом эпизоде состояния s и выбора в нем действия a. Значения, получаемые при использовании этих методов, сходятся квадратично к истинным значениям ожидаемых ценностей, поскольку количество посещений каждой пары состояние – действие приближается к бесконечности.
Единственная сложность заключается в том, что многие пары состояние – действие могут никогда не быть посещены. В случае, когда π – детерминированная стратегия, выгода будет учитываться только для одного из действий каждого состояния. И тогда оценки для других действий не будут улучшаться с опытом, так как значения выгоды не будут усредняться. Вспомним, что целью изучения значений ценности действий является следующее: помощь в выборе действий, доступных в каждом состоянии. Но тогда вышеперечисленное становится серьезной проблемой, так как невозможно сравнить действия между собой, чтобы выбрать наилучшее, поскольку нужно оценить ценность всех действий из каждого состояния, а не только того состояния, которое в данный момент предпочтительно.
Необходимо обеспечить постоянное изучение для того, чтобы оценить через ценность действия стратегию. Чтобы гарантировать, что все пары состояние – действие будут посещены бесконечное число раз при бесконечном числе эпизодов, нужно указать, что первый шаг каждого эпизода начинается в паре состояние – действие и что каждая пара имеет отличную от нуля вероятность быть выбранной в качестве начала. Это называется предположением об изучающих стартах.
К сожалению, на предположение об изучающих стартах нельзя полагаться в целом, так как стартовые условия не всегда могут быть полезны. Например, при обучении непосредственно на основе фактического взаимодействия с окружающей средой. Другим вариантом для обеспечения появления всех пар состояние – действие может быть подход, который заключается в рассмотрении только стохастических стратегий с ненулевой вероятностью выбора всех действий в каждом состоянии.
Рассмотрим, как можно использовать оценку методом Монте-Карло для формирования управлением, то есть для аппроксимации оптимальных стратегий.
Стратегия улучшается в несколько раз, чтобы приблизиться к функции ценности. Но и функция ценности, в свою очередь, постоянно меняется, чтобы наиболее точно приблизиться к текущей стратегии. Каждый из этих двух видов создает постоянно меняющуюся цель друг для друга, то есть в некоторой степени работают друг против друга. Но, несмотря на это, они приближают к оптимальности и функцию ценности, и стратегию.
Сначала рассмотрим метод классической итерации по стратегиям. Будем выполнять чередующиеся шаги: сначала полную ее оценку, затем – полное улучшение стратегии. Начнем с произвольной стратегии π0, а закончим оптимальной стратегией и оптимальной функцией ценности (рис. 1).
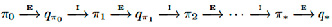
Рис. 1. Схема метода
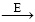 обозначает полную оценку стратегии, а
обозначает полную оценку стратегии, а 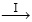 – полное улучшение стратегии. Реализуется много эпизодов, где приблизительная функция ценности действия асимптотически приближается к истинной функции. Предположим, что будем наблюдать бесконечное количество эпизодов и что, кроме того, они будут генерироваться с помощью изучающих стартов. При этих предположениях методы Монте-Карло будут точно вычислять каждое
– полное улучшение стратегии. Реализуется много эпизодов, где приблизительная функция ценности действия асимптотически приближается к истинной функции. Предположим, что будем наблюдать бесконечное количество эпизодов и что, кроме того, они будут генерироваться с помощью изучающих стартов. При этих предположениях методы Монте-Карло будут точно вычислять каждое 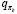 для произвольного πk.
для произвольного πk.
Стратегию можно улучшить, сделав ее «жадной» по отношению к текущей функции ценности. Тогда в данном случае будем иметь функцию действие-ценность, следовательно, чтобы построить «жадную» стратегию, модель не потребуется.
Для любой функции ценность действия q, соответствующей «жадной» стратегии, это такая стратегия, которая для каждого 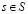 выбирает действие с максимальной ценностью:
выбирает действие с максимальной ценностью:
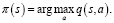
Затем можно улучшить стратегию, построив каждое πk+1 как жадную по отношению к 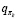 . Для всех
. Для всех 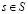
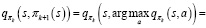
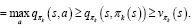
Тогда каждая стратегия πk+1 лучше, чем πk, или равна ей в том случае, если они обе являются оптимальными стратегиями. Это, в свою очередь, гарантирует, что весь процесс сходится к оптимальной стратегии и оптимальной функции ценности.
Таким образом, методы Монте-Карло можно использовать для нахождения оптимальных стратегий, учитывая только выборку эпизодов, при отсутствии других знаний о динамике окружающей среды.
Чтобы понять, как работает метод Монте-Карло на практике, рассмотрим следующий пример. Сыграем в карточную игру блэкджек и вычислим функцию ценности.
Суть игры блэкджек состоит в следующем: необходимо собрать карты таким образом, чтобы сумма была максимальной, но при этом не превышала 21. Король, дама, валет имеют значение 10, туз принимает значения 1 либо 11, тогда он называется играющим. Остальные карты имеют значения согласно своему номиналу. Игрок играет со сдающим, независимо от других участников. В начале игры им обоим раздается по две карты, одна из карт раздающего открывается. Игрок может взять себе еще одну карту, или же он может остановиться. Если он останавливается, то сдающий берет себе карты из колоды до тех пор, пока их сумма не окажется больше или равна 17. Если игрок или сдающий получает в сумме больше 21, то он проигрывает. В остальных случаях выигрывает тот, у кого сумма карт окажется больше, чем у другого. В случае равной суммы – ничья.
Для имитации окружающей среды воспользуемся средой Blackjack библиотеки Gym [3]. Она описывается следующим образом:
1. Каждый эпизод представляет собой марковский процесс принятия решений, в начале которого оба участника получают свои две карты, при этом одна карта сдающего открыта.
2. Эпизод заканчивается в случае, если кто-то выигрывает или игра завершается ничьей. Вознаграждение начисляется в конце эпизода: 1, если игрок выиграл; 0 – ничья; -1, если игрок проиграл.
3. В каждом раунде у игрока есть два действия: получить еще одну карту (1) или больше не брать карт (0).
Посмотрим, как работает данная среда.
Для начала подключим библиотеки PyTorch и Gym и создадим экземпляр окружающей среды Blackjack [4]:
Import torch
import gym
env = gym.make(‘Blackjack-v0’)
Затем приведем среду в исходное состояние командой env.reset() и получим следующий результат (рис. 2).
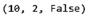
Рис. 2. Исходное состояние
Возвращаются три переменные, которые определяют:
1. Количество очков у игрока – в данном случае 10.
2. Количество очков у сдающего – в данном случае 2.
3. Наличие играющего туза у игрока – в данном случае отсутствует.
Можно попросить еще одну карту командой env.step(1). Получим результат (рис. 3).
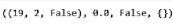
Рис. 3. Результат работы команды
После выполнения данной команды возвращаются три переменные состояния (19, 2, False), вознаграждение, равное нулю в данном случае, и признак завершения эпизода – False. После этого игрок перестает брать карты с помощью команды env.step(0).
После этого к действиям приступает сдающий, и в данном случае игрок проигрывает (рис. 4).
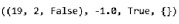
Рис. 4. Завершение игры
Теперь перейдем к предсказанию ценности для простой стратегии, когда игрок перестает брать карты, если он набрал 19 очков.
Для начала напишем функцию, которая имитирует эпизод Blackjack при следовании простой стратегии:
def run_episode(env, hold_score):
state = env.reset()
rewards = []
states = [state]
is_done = False
while not is_done:
action = 1 if state[0] < hold_score else 0
state, reward, is_done, info = env.step(action)
states.append(state)
rewards.append(reward)
if is_done:
break
return states, rewards
Теперь определим функцию, которая оценивает простую стратегию методом Монте-Карло первого посещения:
from collections import defaultdict
def mc_prediction_first_visit(env, hold_score, gamma, n_episode):
V = defaultdict(float)
N = defaultdict(int)
for episode in range(n_episode):
states_t, rewards_t = run_episode(env, hold_score)
return_t = 0
G = {}
for state_t, reward_t in zip(states_t[1::-1], rewards_t[::-1]):
return_t = gamma * return_t + reward_t
G[state_t] = return_t
for state, return_t in G.items():
if state[0] <= 21:
V[state] += return_t
N[state] += 1
for state in V:
V[state] = V[state] / N[state]
return V
Данная функция выполняет следующие действия [5]:
1. Прогоняет n_episode эпизодов, следуя простой стратегии.
2. Вычисляет доходы при первом посещении каждого состояния в каждом эпизоде.
3. Усредняет доходы, полученные при первом посещении каждого состояния по всем эпизодам, вычисляя тем самым ценность. Состояния, в которых игрок набрал больше 21 очка, игнорируются, так как вознаграждение в них равно -1.
Далее задаются начальные параметры игры: количество очков, при которых игра останавливается, равное 19; коэффициент обесценивания 1; количество эпизодов 500000:
hold_score = 19,
gamma = 1,
n_episode = 500000.
Выполним предсказание методом Монте-Карло с данными параметрами, распечатаем получившуюся функцию ценности, выведем количество состояний (рис. 5):
value = mc_prediction_first_visit(env, hold_score, gamma, n_episode)
print(‘Функция ценности, вычисленная методом МК первого посещения:\n’,
value)
print(‘Количество состояний:’, len(value))

Рис. 5. Результат работы программы
Заключение
Проведенное исследование дало возможность показать, насколько эффективно можно вычислить функцию ценности 280 состояний в среде BlackJack с помощью предсказания методом Монте-Карло. При этом был применен нестандартный подход к обучению с заранее неизвестными обучающими примерами, которые подбирались автоматически, в процессе оптимизации.
Приведены возможные пути улучшения стратегии:
− Увеличение числа оптимизируемых параметров.
− Применение других способов вознаграждения агента.
− Создание нескольких конкурирующих между собой агентов для увеличения пространства вариантов.


 science-review.ru
science-review.ru