В отличие от AISD, где каждый документ пишется одним автором, AIMD фокусируется на работе с документами, написанными несколькими авторами. Решения AIMD имеют ряд ограничений: лучшие решения AIMD на основе стилометрии имеют низкую точность; увеличение числа соавторов текстов негативно влияет на производительность решений AIMD; и решения AIMD не были предназначены для работы с непишущими авторами (non-writing authors – NWA). Тем не менее NWA существуют в реальных случаях, то есть существуют тексты, для которых не каждый из перечисленных соавторов внес свой вклад в качестве автора.
Цель исследования – изучить способы определения авторства текста с несколькими авторами.
Предложенное решение
Часть предварительной обработки фреймворка отвечает за три основных процесса: извлечение признаков, построение графа соавторства (Co-Authorship Graph – CAG) и обучение CAG. Для процесса извлечения признаков каждый документ с несколькими авторами представляется в виде набора фрагментов (т.е. коллекции наборов точек). Каждая точка данных рассчитывается из 500 токенов, с использованием 56 стилометрических признаков [1].
После завершения процесса выделения признаков CAG строится таким образом, чтобы каждая вершина представляла фрагмент, а наличие ребра между двумя вершинами означало, что они стилистически похожи. После завершения построения CAG обучение производится таким образом, чтобы каждый фрагмент отражал только своего истинного автора (авторов). Структура CAG представлена на рис. 1.
После того как часть предварительной обработки была завершена, полученные в ходе обучения данные используются для создания прогноза нескольких авторов для любого заданного документа [2]. Чтобы получить вероятностный прогноз для данной выборки, используются вероятностные метки стилистически похожих выборок. Таким образом, эффективно фиксируется совместный характер документа как в тестовом, так и в обучающем наборе текстов.
Как объяснялось ранее, каждый документ в корпусе представляется в виде набора фрагментов, где каждый фрагмент представлен как набор точек [3]. Есть две основные причины для представления каждого документа в виде коллекции наборов точек. Это позволяет нам приписывать различные фрагменты одного и того же документа их первоначальным авторам, а также применять установленные меры подобия, связанные с методами обработки выбросов, такими как модифицированное расстояние Хаусдорфа (modified Hausdorff distance – MHD), что может помочь улучшить общую производительность.
Чтобы получить достоверную стилистическую информацию из каждой точки данных, размер устанавливается равным 500 токенам. Однако использование 500 токенов на фрагмент дает только 24 точки данных для документа с 12000 токенов, чего недостаточно для стилометрического анализа. Чтобы преодолеть эту проблему, применяется концепция скользящего окна для создания точек данных с перекрывающимися последовательностями токенов. Этот процесс проиллюстрирован на рис. 2. Например, используя 500 токенов в качестве размера скользящего окна и 50 токенов в качестве приращения скользящего окна, мы можем создать 231 точку данных для каждого документа с 12 000 токенов. Этот же принцип применяется на уровне фрагментов, чтобы получить достаточное количество фрагментов для проведения анализа. В частности, установив размер фрагмента на 6 точек данных и значение приращения скользящего окна на 2, мы можем сгенерировать 113 фрагментов для каждого документа с 12 000 токенов.
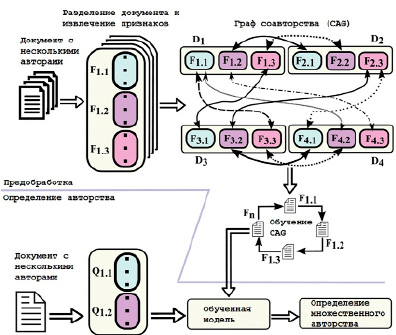
Рис. 1. Структура предложенной модели CAG
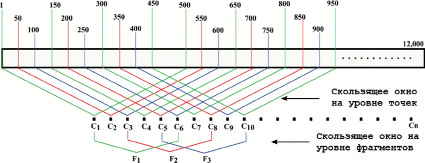
Рис. 2. Получение стилистической информации
В данной работе для обработки документов с несколькими авторами используются символьные n-граммы переменной длины [4]. После того как измеряются их показатели tf-idf, n-граммы ранжируются в порядке убывания в соответствии с их показателями tf-idf, чтобы выбрать 500 лучших n-грамм для использования в качестве признаков вместе с предыдущим пространством признаков.
Символьные n-граммы представляют собой непрерывную последовательность из n символов из образца текста. Доказано, что признаки на основе n-грамм хорошо работают при решении проблем идентификации авторства независимо от длины текстовых образцов. В частности, n-граммы символов могут эффективно фиксировать стилистическую информацию авторов из небольших образцов текста (например, 500 токенов) [5] по сравнению с функциями, основанными на словарном запасе. Характеристики символьной n-граммы обеспечивают наилучшие результаты, когда значение n равно 5, 4 или 3 [6]. Особенности n-граммы символов могут фиксировать сложную стилистическую информацию об авторах на синтаксическом, структурном и лексическом уровнях. Символьные n-граммы могут допускать шум в текстовых образцах. Извлечение символьных n-грамм не требует токенизаторов, теггировщиков, синтаксических анализаторов или каких-либо языково-зависимых и нетривиальных инструментов обработки текста, что делает их пригодными для выполнения многоязычных задач атрибуции авторства.
Создание CAG
Одна из основных проблем, связанных с проблемой AIMD, заключается в том, что каждый документ связан с несколькими авторами. Из-за своей комбинаторной природы один и тот же список авторов не может повторяться в корпусе документов с несколькими авторами, что усложняет моделирование этой проблемы. Более того, в документе с несколькими авторами (например, в научной статье) некоторые из авторов могут не участвовать в написании самой статьи (NWA). То есть в задачах AIMD отсутствует базовая истинная информация, что усложняет решение этой проблемы. Таким образом, метод прогнозирования AIMD должен быть способен делать выводы об авторстве документа с несколькими авторами без абсолютной достоверной информации.
Предлагаемая структура AIMD основана на наблюдении, что стилистически похожие фрагменты, вероятно, были написаны аналогичной группой авторов [7]. Чтобы зафиксировать стилистическое сходство фрагментов документов, предлагается структура данных, называемая графом соавторства (CAG). Кроме того, предлагается итеративный алгоритм для идентификации оригинального автора каждого фрагмента документа.
После завершения процесса извлечения признаков строится граф соавторства (CAG), в котором каждая вершина представляет собой фрагмент, а ребро между двумя вершинами показывает, что они стилистически похожи. Для построения ребер CAG для каждого фрагмента идентифицируются k стилистически похожих фрагментов, где в качестве расстояния используется модифицированное расстояние Хаусдорфа. Эти ближайшие соседи – вершины графа, а MHD-расстояния – веса ребер. Предполагается, что каждый фрагмент документа связан со списком авторов из документа, который может включать одного или нескольких авторов. Список инициализируется путем назначения равной вероятности каждому автору.
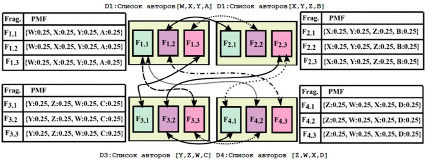
Рис. 3. Визуализация графа соавторства четырех текстов с четырьмя авторами
Обучение CAG
Теперь объясним процесс обучения CAG на примере, показанном на рис. 3. Имеется четыре документа, каждый связан с четырьмя авторами. Мы устанавливаем информацию об истинности данных следующим образом. Во-первых, предположим, что только первые три автора каждого документа внесли свой вклад в написание текста. Например, для документа D1 только авторы W, X и Y написали части документа D1, в то время как автор A был непишущим автором. Точно так же B, C и D являются NWA для D2, D3 и D4 соответственно, эта основная истинная информация скрыта от модели.
Поскольку основная информация о непишущих авторах скрыта от модели, каждый фрагмент документа [8] связывается со всеми перечисленными соавторами с равной распределенной вероятностью. Например, авторские PMF F1.1, F1.2, F1.3 являются однородными {W:0,25, X:0,25, Y:0,25, Z:0,25}. Таким же образом выводим начальные PMF остальных фрагментов, показанных на рис. 3.
Алгоритм построения CAG возвращает ребра, соединяющие стилистически похожие фрагменты. Например, по выявленным ребрам графа видно, что фрагмент F1.1 стилистически похож на F3.3 и F4.2. Точно так же F1.2 стилистически похож на F2.1 и F4.3. Несмотря на то, что каждый фрагмент в документе инициализируется с равной вероятностью, распределенной между всеми соавторами, они связаны с разными наборами стилистически сходных фрагментов, связанных с разными соавторами.
Алгоритм обучения CAG преследует две основные цели: изменить PMF каждого фрагмента таким образом, чтобы он отражал истинного автора (авторов) этого фрагмента, и исключить непишущих авторов из списка. Один и тот же алгоритм выполняется в каждой вершине корпуса с несколькими итерациями, называемыми супершагами. В этом алгоритме каждая вершина отмечает k наиболее похожих фрагментов в качестве соседей. Этот алгоритм состоит из трех основных частей: получение, вычисление и отправка.
На каждом супершаге применяется тот же процесс, супершаги повторяются до тех пор, пока все PMF не сойдутся или количество итераций не достигнет заданного значения.
Пример
Рассмотрим теперь, как работает обучение в контексте примера, приведенного на рис. 3. Фрагмент F1.1 получает два PMF от двух своих соседей F3.3 и F4.2 как {Y:0,25, Z:0,25, W:0,25, C:0,25} и {Z:0,25, W:0,25, X:0,25, D:0,25} соответственно. Затем сравниваются PMF каждого фрагмента (соседнего) со списком соавторов [W, X, Y, A], чтобы удалить авторов, которые не указаны в списке F1.1. В этом примере авторы Z и C исключены из фрагмента F3.3. Точно так же авторы Z и D исключаются из фрагмента F4.2. После исключения авторов, которых нет в списке соавторов F1.1, повторно нормализуем PMF. Повторная нормализация приводит к {Y:0,5, W:0,5} как PMF для F3.3 и {W:0,5, X:0,5} как PMF для F4.2. Для простоты изложения предположим, что два ближайших соседа находятся на одинаковом расстоянии от соответствующего фрагмента и вносят одинаковый вклад в PMF фрагмента. Следовательно, средневзвешенное значение двух PMF равно {W:0,5, X:0,25, Y:0,25} после первого супершага.
Следуя тому же процессу, получаем
1. {W:0,25, X:0,5, Y:0,25} для F1.2,
{W:0,25, X:0,25, Y:0,5} для F1.3.
2. {X:0,5, Y:0,25, Z:0,25} для F2.1,
{X:0,25, Y:0,5, Z:0,25} для F2.2,
{X:0,25, Y:0,25, Z:0,5} для F2.3.
3. {Y:0,5, Z:0,25, W:0,25} для F3.1,
{Y:0,25, Z:0,5, W:0,25} для F3.2,
{Y:0,25, Z:0,25, W:0,5} для F3.3.
4. {Z:0,5, W:0,25, X:0,25} для F4.1,
{Z:0,25, W:0,5, X:0,25} для F4.2,
{Z:0,25, W:0,25, X:0,5} для F4.3.
Как видно, все PMF становятся менее однородными только после первого супершага. Для каждого документа PMF сходятся к следующим значениям.
1. Документ D1: {W:1} для F1.1,
{X:1} для F1.2, и {Y:1} для F1.3.
2. Документ D2: {X:1} для F2.1,
{Y:1} для F2.2, и {Z:1} для F2.3.
3. Документ D3: {Y:1} для F3.1,
{Z:1} для F3.2, и {W:1} для F3.3.
4. Документ D4: {Z:1} для F4.1,
{W:1} для F4.2, и{X:1} для F4.3.
NWA каждого документа не включены в PMF, а списки авторов D1, D2 и D3 правильно определены как [W, X, Y], [X, Y, Z], [Y, Z, W] и [Z, W, X] соответственно.
Заключение
В этом исследовании предложен эффективный и масштабируемый подход для идентификации авторства документов с несколькими авторами. Основное преимущество предлагаемой структуры заключается в ее способности вероятностно приписывать различные фрагменты (части) одного и того же документа с несколькими авторами разным авторам. В частности, структура может фиксировать стилистическое сходство между парами фрагментов во всем корпусе документов. Кроме того, алгоритм обучения графа эффективен при изучении истинного автора (авторов) каждого фрагмента и определении NWA документов с несколькими авторами.


 science-review.ru
science-review.ru