Музыка как художественная форма содержит в себе эмоцию и идею композитора. Первая музыка, написанная с помощью компьютера, появилась в 1957 г., и с тех пор все больше и больше музыки создавалось с использованием компьютерной техники. Существует множество методов алгоритмического создания музыки: основанные на грамматике, марковские модели и нейронные сети. Преимуществом использования глубокого обучения (включая машинное обучение) для создания музыкального контента является его универсальность. По сравнению с другими методами система, основанная на машинном обучении, способна изучать модель из произвольного набора музыкальных произведений.
Цель исследования – рассмотреть модель глубокого обучения для создания полифонической музыки, основанную на близких нотах, которые окружают целевую ноту во временном измерении и измерении ноты. Как и большинство исследований, данная работа подразумевает представление музыкальных данных в MIDI формате. Для эффективности генерации модель генерирует только ноты и игнорирует музыкальное исполнение, такое как скорость.
Основные особенности рассматриваемого метода. Многие исследователи рассматривают задачу генерации музыки как вероятностную модель полифонической музыки, они представляют музыку как последовательность нот и пытаются моделировать музыку как распределение вероятностей, где следующая нота назначается на основе вероятностей предыдущей последовательности нот и некоторого контекста, такого как аккорд, гамма, ритм [1, 2]. Важно отметить, что, по сравнению с композицией на основе правил, конкретную модель можно обучать на основе большого количества музыкальных произведений и позволять ей автоматически обнаруживать закономерности. На этапе генерации создается выборка из обученного распределения вероятностей для создания новых музыкальных произведений. Рекуррентные нейронные сети (RNN), особенно сети с долговременной кратковременной памятью (LSTM), эффективно предсказывают данные временных рядов. Многие исследователи использовали LSTM для создания музыки, что дало хорошие результаты.
Основной идеей этого метода является введение двунаправленной рекуррентной сети по оси заметок и оси времени. Интуитивное объяснение состоит в том, что, когда композиторы сочиняют песни, они будут рассматривать ноты с глобальной точки зрения, и на каждую ноту будут влиять окружающие ноты и гармоники. Поэтому моделируется условная вероятность по двунаправленной оси нот, которая представляет гармонические отношения, и условная вероятность по двунаправленной оси времени, которая представляет окружающие ноты. Эта модель способна генерировать музыку, лежащую в основе теории музыки и латентных паттернов в музыкальных произведениях. Основные нововведения:
− Вместо однонаправленной сети использовать двунаправленную рекуррентную нейронную сеть для генерации последовательности нот как по оси нот, так и по оси времени.
− Рассмотрение улучшенной функции потерь, чтобы избежать множества бессмысленных результатов.
− Упрощенное представление входных данных и новая стратегия выборки.
Входные данные. Музыка состоит из нескольких дорожек, а дорожка содержит несколько нот. Мелодия может рассматриваться как особая дорожка и обычно является самой важной частью музыки, в этой статье используется модель для создания одной дорожки мелодии, которая позволяет одновременно воспроизводить несколько нот. Целесообразно использовать пиано-ролл (piano roll) для представления музыки. Пианино-ролл (piano roll) – это матрица N * T * C, N – количество шагов (N равно 128 в MIDI, шаг от 0 до 127), T – длина последовательности и количество шагов по времени, C равно 2 в этой статье. В каждой ячейке в матрице хранятся два значения, первое значение представляет, что нота играется (1 играется, а 0 не играется), второе значение представляет, что нота артикулирована (1 артикулируется, а 0 нет). На рис. 1 показано простое представление пиано-ролла.
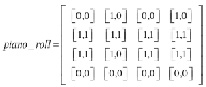
Рис. 1. Простой пример представления пиано-ролла
В MIDI нота представляет собой кортеж, например <скорость (velocity), высота ноты (pitch), начало ноты (start), конец ноты (end)>, в данной статье параметр скорости (velocity) не учитывается. Скорость (velocity) – это скалярное значение (диапазон от 0 до 127 в MIDI), которое обычно устанавливается на общую громкость воспроизводимой ноты, но это значение неверно во многих MIDI-файлах [3]. Поэтому в статье игнорируется скорость и принимается постоянным значением.
В теории музыки и в MIDI формате октава состоит из 12 полутонов, поэтому можно использовать вектор размером 12, представляющий октаву, которая описана следующим образом (рис. 2).
Трезвучие – это набор из трех нот, которые можно складывать вертикально в терции, и функция трезвучия определяется его качеством: мажор, минор, уменьшенное или увеличенное [4]. Для всех мажорных аккордов представление отличается только смещением, которое называется «трансляционной инвариантностью». Вдохновляясь принципом сверхточных нейронных сетей для получения инвариантности к сдвигу, можно использовать связанные веса для достижения свойства инвариантности к переводу.

Рис. 2. Представление аккордов Dm, Em, Cm
Берется двухбитный пианино-ролл, представляющий музыку, первые биты обозначают, что проигрывается текущая нота в текущее время, а вторые обозначают удерживаемую ноту (новая нота нажимается, если ее значение равно 1, иначе продолжается).
Ввод разработан на основе двух концепций.
− Контекст аккорда: мелодия и аккорд находятся в гармонии, между ними много общих тонов, поэтому целесообразно использовать вектор размером 12 для обозначения аккорда, который поддерживает пользовательский ввод во время создания музыки и позволяет пользователю взаимодействовать с музыкой. На этапе обучения рассматривается сочетание высот между басовым голосом как аккорд в одном такте.
− Ближайший контекст: каждый элемент в последовательности является 2-битным, поэтому используется many-hot с длиной 50 для обозначения контекста окрестности.
Наконец, ввод направления времени представляет собой комбинацию контекста аккорда и контекста окрестности. В направлении ноты используется вывод направления времени и вывод предыдущей ноты в качестве текущего ввода.
Архитектура. Модель архитектуры базируется на двухосной LSTM, которая обеспечивает высокую производительность при музыкальном прогнозировании [5]. Архитектура разделена на две части: генерация контекста заметок во временном направлении и генерация заметок в направлении заметок.
Во временном направлении назначается один сетевой экземпляр каждой заметке. Чтобы обеспечить «свойство инвариантности перевода», каждый экземпляр сети будет иметь связанные веса, и каждая заметка будет получать свои выходные данные в одной и той же процедуре расчета. Кроме того, использование связанных весов заметно уменьшит количество параметров в системе и снизит риск переобучения.
Схема привязанных весов следующая: на временном шаге t последовательность заметок принимается как V = {v1, v2, v3, v4, v5}, сеть LSTM будет обучаться на V.
На рис. 3 три сети LSTM будут иметь одинаковые веса, и при сложении двух слоев LSTM будет увеличиваться пропускная способность сети. Кроме того, двунаправленная LSTM хорошо подходит для создания гармонической мелодии, например, если модель обучается только с данными положительного направления, что означает, что текущая нота будет определяться только предыдущими появившимися нотами, некоторые ноты не будут гармоничны с точки зрения негативного направления [6]. Двусторонняя стрелка на рис. 3 показывает, что сеть является двунаправленной. Путем объединения прямой и обратной информации модель создает гармоничную музыку.
Наконец, как только контекст ноты обучен системой, можно легко получить окончательную вероятность воспроизведения ноты. На каждом временном шаге окончательные активации текущей заметки определяются тремя элементами: контекстом заметки, предыдущими активациями и следующими активациями, поэтому они объединяются с вектором ввода LSTM. То же самое с направлением времени, складываются 2 слоя LSTM. Полная архитектура показана ниже (рис. 4), она содержит направление времени и направление нот.
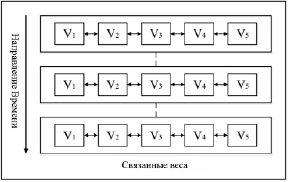
Рис. 3. Связанные веса во временном направлении
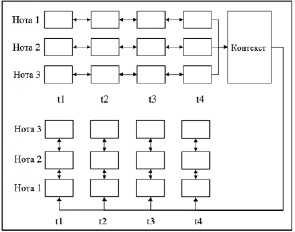
Рис. 4. Полная архитектура сети
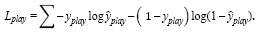 (1)
(1)
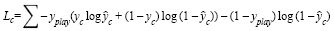 . (2)
. (2)
По сравнению с двухосевой сетью LSTM, данная архитектура изменяет форму входных данных и позволяет пользователю настраивать ход и гиперпараметры сети. Прежде всего, двунаправленная LSTM решает проблемы гармонии нот и улучшает производительность двухосевой LSTM.
Функция потери. На каждом временном шаге модель выводит два результата: вероятность воспроизведения и вероятность продолжения для каждой ноты. Двухосевая модель LSTM добавляет слой активации softmax для каждого выхода, а функция потерь представляет собой двоичную кросс-энтропию [7]. Принимаются 2-битные числа, многие из которых представляют пиано-ролл, однако если воспроизводимый бит принимается равным 0, а продолжающийся бит равен 1, то эта нота не имеет смысловой нагрузки. Таким образом, сумма бинарных кросс-энтропийных потерь даст много одинаковых, бессмысленных результатов. Для решения этой задачи вводятся функции потерь для сыгранного бита (1).
Формула (1) представляет собой нормальную потерю перекрестной энтропии, она измеряет расстояние между истинным значением и прогнозируемым значением. Как только бит воспроизведения определен, потеря продолжающегося бита является явной. Далее переопределяется Lc , который обозначает потерю между прогнозируемой вероятностью и реальной продолжительностью бита (2).
Формула (2) состоит из двух частей: первая часть обозначает потерю перекрестной энтропии бита продолжения при воспроизведении текущей ноты, а вторая часть ограничивает бит продолжения равным 0, если текущая нота не воспроизводится. Этот подход позволяет избежать множества бессмысленных результатов.
Тренировка и генерация. Модель обучается оптимизатором Адама, размер партии составляет 64, все слои LSTM сложены по 2, а размер единиц LSTM составляет 512. Чтобы предотвратить переобучение, нужно досрочно прекращать обучение, если потери при проверке больше не уменьшаются.
После того как модель была обучена, можно сгенерировать последовательность заметок следующим образом:
− Во-первых, случайным образом генерируется начальный ввод (или пользовательский ввод) и подается в сеть во времени, что выводит контекст на текущем временном шаге.
− Во-вторых, подается контекст на текущем временном шаге и предыдущих выбранных нотах (предыдущая из первой ноты является нулевым вектором) в сеть по направлению ноты и выводится условная вероятность воспроизведения и продолжения.
− Наконец, выбирается текущая заметка через выборочную стратегию по текущей условной вероятности.
− После завершения генерации заметки в течение одного временного шага модель обновит ввод первого шага и повторит процесс генерации.
Путем пошаговой итерации по направлению ноты и направлению времени модель может генерировать произвольное полиномическое музыкальное время шаг за шагом. Несмотря на то, что для генерации мелодии используется многократная итерация, занимающая много времени, общая производительность повышается [8].
Стратегия выборки. На этапе генерации на каждом временном шаге t последовательность нот принимается как V(t), для каждой ноты n вероятность воспроизведения ноты (или вероятность продолжения воспроизведения) принимается как p(t,n). Таким образом, окончательный вывод текущей позиции следует выбирать на основе p(t,n), для решения этой проблемы используется выборочная стратегия. Рассматривается вероятность сыгранной ноты как распределение Бернулли, случайным образом выбираемое значение посредством выборки, обусловленной p(t,n). Как следствие, музыкальный контент меняется каждый раз, даже если одни и те же входные данные подаются в сеть с помощью стратегии сэмплирования.
Заключение
Генеративная музыка становится все более востребованной, она хороша не только для персонального пользования, но, к примеру, для использования на фоне в видеоролике или видеоигре. Современные модели способны создавать самые разные композиции в различных жанрах на любой вкус, рассмотренная в этой статье двунаправленная рекуррентная сеть позволяет эффективно генерировать гармоничную музыку, которую можно использовать в бизнесе, не тратя большие деньги на авторские композиции и не нарушая авторские права.


 science-review.ru
science-review.ru