Scientific journal

Scientific Review. Technical science

ISSN 2500-0799

ПИ №ФС77-57440

Классические методы оценки энергетических спектров дискретных сигналов обычно основаны на применении процедур, использующих численные методы быстрых преобразований Фурье (БПФ). Они эффективны в вычислительном отношении и обеспечивают получение асимптотически достоверных оценок для весьма обширного класса сигналов, удовлетворяющих гипотезе стационарности, эргодичности и ограничению выборки большого объема [1]. При проведении анализа взаимного влияния сигналов необходима разработка математической модели анализируемого случайного процесса.

На первый взгляд при анализе спектра сигнала с квадратурной амплитудной модуляцией (КАМ) создается впечатление, что спектр сигнала состоит из одной спектральной составляющей, так как итоговый модулированный сигнал состоит из «кусочков» одной гармонической составляющей, отличающихся амплитудой и фазой, однако при анализе спектров численным методом Прони выявляется достаточно широкий спектр, оказывающий влияние на соседние каналы. Применительно к численным методам математического моделирования различают следующие типы моделей: АR-модель («авторегрессия»), MA-модель («скользящее среднее»), ARMA-модель. Наибольшее распространение получили методы, основанные на АR-модели формирования сигнала [2].

Статистические характеристики спектральных АР-оценок мало исследованы, и большая часть имеющихся сведений основана на результатах экспериментов, полученных путем моделирования. Для оценки АR-параметров используются метод Юла – Уокера, ковариационный метод, модифицированный ковариационный метод, метод Берга [3].

Затруднение в теории спектрального анализа вызывает определение совокупного спектра сигнала, включающего помеху «белый шум» и помеху, вызванную соседними каналами многоканальной телекоммуникационной системы (ТКС). Методический аппарат, позволяющий проводить такую оценку на основе БПФ или численных методов, требует сложных вычислений и технически сложно реализуем [1]. Использование коэффициента взаимного влияния сигналов в многомерных метрических пространствах [4] позволит решить эту научную проблему.

Попытки научного обоснования и расчета спектров в основном базируются на различных эмпирических опытах, а не на фундаментальной теоретической основе. Публикации новых методов спектрального оценивания нередко сопровождаются субъективными описаниями достигаемых на их основе характеристик, ожидающихся в результате ограниченного числа испытаний. Превосходство того или иного метода спектрального анализа определяется преимуществом или компромиссом, применительно к видам сигналов, длительности наблюдения, точности оценки, временным и аппаратурным затратам на получение результатов [5].

Цель исследования – разработать модифицированный сегментированный численный метод Прони с учетом взаимного влияния сигналов в многоканальной телекоммуникационной системе.

Материалы и методы исследования

Относительное превосходство того или иного метода спектрального анализа определяется необходимостью выделения того или иного преимущества, применительно к видам сигналов: длительности наблюдения, точности оценки, временных и аппаратурных затрат на получение результатов.

Метод Прони – это метод моделирования выборочных данных в виде линейной комбинации экспоненциальных функций [6, 7].

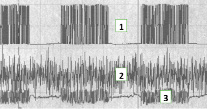
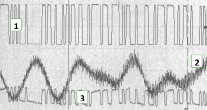
На рис. 1, а, представлены осциллограмма модуляции и демодуляции сигналов с КАМ-64, соответственно цифровой код (слово) содержит 6 символов. Осуществляется пакетный способ передачи. Причем цифрой 1 обозначен цифровой сигнал Манчестерского кода, поступающий на вход модема. Цифрой 2 обозначен сигнал с КАМ, поступающий из линии связи (радио или проводной) в демодулятор. Цифрой 3 обозначен выходной сигнал демодулятора, поступающий в оконечную аппаратуру. На рисунке 1, б, представлены осциллограммы модуляции и демодуляции сигналов КАМ с «белым» шумом и с помехой по соседнему каналу развернутого пакета.

а)

б)

Рис. 1. Осциллограммы модуляции и демодуляции сигналов с КАМ-64

Анализ осциллограмм показывает, что демодулированный сигнал претерпевает искажения формы.

Одним из допущений при разработке алгоритма обработки сигналов по методу Прони является предположение о точно известном времени начала сигнала. Если начало сигнала известно точно, тогда требуется оценить только амплитуду A сигнала, постоянную затухания α, частоту ω и фазу φ. В случае нескольких синусоид, помимо параметров каждой, дополнительно требуется оценить и их число [8]. Чтобы использовать метод Прони для представленного на рисунке 1, б, сигнала с «белым» шумом и помехой по соседним каналам, необходимо учитывать: какой длительности необходимо выбирать окно обработки; как устанавливать окно обработки (как определить начало исследуемого сигнала); как работает алгоритм, при взаимном влиянии сигналов.

Результаты исследования и их обсуждение

Исходя из общих принципов обработки сигнала, можно предложить следующую модификацию метода Прони. Длительность окна обработки принимается равной отрезку времени, в котором сосредоточен модулированный сигнал одного пакета (рис. 1), при условии, что начало окна обработки совпадает с началом первого сегмента сигнального созвездия с определенным уровнем КАМ. Первый сегмент определяется фронтом первого бита первого цифрового кода информационного пакета. Окончание окна совпадает со спадом последнего бита цифрового кода информационного пакета.

Следующий этап обработки начинается с поступлением фронта первого цифрового бита последующего цифрового кода информационного пакета, то есть окно обработки сдвигается на один цифровой информационный пакет. Процедура получения спектра сигнала методом Прони заключается в накоплении данных о спектральных составляющих модулированных цифровых слов информационного пакета (окна обработки). Далее полученные данные о спектральных составляющих обрабатываются с целью выявления составляющих, влияющих на соседний канал.

Никаких «априорных» ограничений на выбор сегментов не накладывается, и они содержат достаточное количество точек данных (> 20).

Таким образом, можно выполнять спектральный анализ очень коротких временных рядов с нестационарными процессами с помощью метода сегментации. Тогда для оценки спектров мощности различных сегментов необходима минимизация с ограничениями по методу наименьших квадратов. В научных исследованиях этот подход обозначен как «сегментированный метод Прони» (СМП) [7].

Предположим, что наблюдаемый процесс (окно обработки t0, tN-1), т. е. конечное время серии yn с n = 0, 1, 2, ..., N – 1, может быть разбито на s отрезков (tn, tn + 1), где ni+1 > ni и i = 1, 2, ..., s, таких что в каждом из них процесс можно считать асимптотически стационарным и каждый отрезок данных относительно времени tn = n?t – это элемент сигнала с КАМ, определяемый соответствующим цифровым кодом, определяющим слово в информационной цифровой последовательности, может быть представлено суммой q экспоненциально затухающих синусоид:

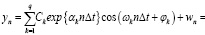
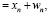(1)

где хп – неизвестный детерминированный сигнал, определяемый одним из отрезков n, а wn – белый шум со средним нулем и дисперсией σ2. Ck, ωk, φk и αk – амплитуды, частоты, фазы и коэффициенты затухания различных компонентов отрезка хп соответственно.

Можно показать, что хn удовлетворяет разностному уравнению

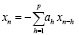(2)

при р = 2q, ассоциированное характеристическое уравнение которого имеет вид

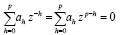(3)

(при а0 = 1). Оценки Прони частот и коэффициентов затухания являются функциями корней характеристического уравнения (2), и автоковариационная функция (где преобразование Фурье является спектром авторегрессии) является решением этого уравнения.

Как следствие из уравнения (3), для наблюдаемого ряда имеем

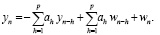(4)

Это стохастическая модель с авторегрессионным скользящим средним (ARMA) для у с равными коэффициентами AR и МА ah, которые связаны с параметрами, появляющимся в уравнении (4).

В статистическом анализе временных рядов модели с АRМА обеспечивают описание стационарного случайного процесса в терминах двух полиномов, один для авторегрессии (AR), а второй для скользящего среднего (МА).

Значения этих параметров вычисляются из комплексных корней zk характеристического уравнения (4). Появление действительных корней будет означать, что некоторые компоненты не имеют колебательного вида, и поэтому они не будут включены в модель. Частоты и константы электронного сворачивания получены путем

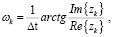(5)

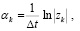(6)

при k = 1, 2, ..., qс, где qc ≤ q – число пар комплексных cопряженных корней. Затем фазы и амплитуды оцениваются путем подстановки значений wk и αk в уравнение (1), и решение задачи наименьших квадратов для всех N данных точек будет иметь вид (7).

Необходимо получить оценку коэффициентов ah в зависимости от варианта модели р. Следовательно, значения Ck, φk, ωk и αk не всегда имеют желаемую точность. Затем необходимо вычислить новый временной ряд хn» для детерминированной части уравнения (1) с оценочными значениями параметров. Когда при вычислении хn можно использовать ряд компонент qs ≤ qc, введение некоторых критериев выбора (например, значения wk должны находиться внутри заданного интервала или значения Ck должны быть больше фиксированного порога). Эта возможность будет очень полезна для игнорирования компонентов, в основном связанных с шумом или с физически несущественными частотами.

Также можно вычислить энергетический спектр сигнала, комбинируя вклады различных компонентов в каждую частоту. Для этого расчета необходимо знать аналитическое выражение для энергетического спектра каждой компоненты, которое легко вычислить с помощью преобразования Фурье затухающей синусоиды. Однако результат зависит от предполагаемого сигнала до и после наблюдаемого временного интервала, для которого нет никакой информации.

Модулированный информационный цифровой пакет содержит X сегментов, каждый из которых содержит достаточное количество точек данных (> 20) для получения достоверной оценки коэффициентов АR.

Предполагается, что наблюдаемый процесс является локально асимптотически стационарным, то есть интервал наблюдения во временной области может быть разделен на отрезки, достаточно короткие, чтобы процесс можно было характеризовать определенной спектральной плотностью мощности.

Фактически для получения значимых результатов стандартные методы Фурье предполагают медленное изменение частотных характеристик процесса во времени. В нашем подходе спектральная плотность не меняется на каждом отрезке, а может резко меняться при переходе от одного отрезка к другому. Ограничимся рассмотрением последовательных и непересекающихся отрезков (модулированных слов сигнального созвездия). Предположим, что найдена правильная сегментация, к каждому сегменту применяются первые две части метода Прони для оценки коэффициентов затухания частот ωd. Затем ко всем данным подгоняется глобальная модель для вычисления амплитуд и фаз. На этом шаге могут быть заданы заданные пользователем условия непрерывности сигнала и его производных до порядка r в точках сегментации tm. Тогда мы должны построить линейную систему наименьших квадратов с ограничениями:

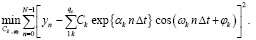(7)

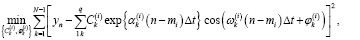(8)

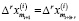
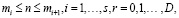
где ? – разностный оператор ?хn = хn – хn-1 с условием, что ?0 – тождественный оператор, а 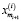– оператор экстраполированного значения следующих шагов.

Оценку спектральной плотности энергии можно производить, начиная непосредственно с аналитического выражения (1), пренебрегая шумом wn. Однако затухающую синусоидальную модель нельзя считать хорошей при произвольных значениях nΔt, поскольку амплитуда компоненты будет неограниченно возрастать либо в прошлом (ak < 0), либо в будущем (ak > 0).

Нужно наложить ограничения на модель для вычисления преобразования Фурье.

При условии, что ak < 0 для каждого k, можно считать, что амплитуды всех компонент тождественно равны нулю для всех моментов времени до начального. В этом случае энергетический спектр:

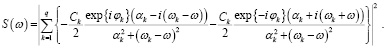(9)

Другая гипотеза предложена Марпл-мл. (1981), которая предполагает, что все компоненты симметрично затухают относительно начала координат. Соответствующий энергетический спектр

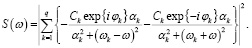(10)

В выражении 3.29 в проблеме взаимного влияния сигналов вызывает интерес помеха wn. В проводимых исследованиях помеха рассматривалась как «белый шум». Для оценки взаимного влияния сигналов помеху необходимо рассматривать как часть энергетического спектра одного канала, находящегося в полосе частот другого канала (рис. 2).

Эрмитова матрица, учитывающая взаимное влияние сигналов, может быть представлена как

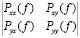(11)

и по определению является матрицей многоканальной спектральной плотности мощности (СПМ) многоканального случайного процесса. Диагональными элементами ее являются автоспектральные плотности отдельных каналов, а недиагональными – взаимные спектральные плотности пар каналов. Заметим, что матрица Рхх(f) эрмитова, т. е. Рхх(f) = Pнхх(f), и является положительно полуопределенной.

Двухканальная взаимная спектральная плотность мощности представляет собой дискретно-временное преобразование Фурье (ДВПФ) взаимной корреляционной функции

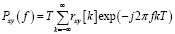(12)

Значения взаимного спектра на каждой частоте не превышают среднего геометрического значения спектров процессов х и у на этой частоте, т. е.

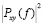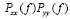≤ (13)

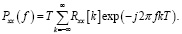(14)

Взаимное влияние по соседнему каналу будет определяться как

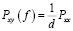, (15)

где d – коэффициент взаимного влияния сигналов, в соответствии с математическими моделями [4, 9].

Тогда Эрмитова матрица, учитывающая взаимное влияние сигналов с использованием многомерных метрических пространств, может быть представлена как

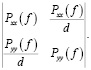(16)

Это матрица когерентности должна иметь неотрицательный детерминант для всех частот. Тогда квадрат модуля когерентности (КМК) может быть представлен в виде

КМК(f)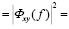

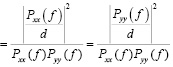(17)

и фазовый спектр когерентности или «фазовый» спектр взаимного влияния сигналов:

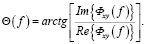(18)

Параметры взаимного влияния спектров сигналов

Величина КМК должна быть заключена между 0 (для частот, на которых отсутствует когерентность между каналами) и 1 (для частот, на которых каналы полностью когерентны в границах некоторых фиксированных фазовых соотношений). Таким образом, КМК можно использовать как для измерения сходства (как функции частоты) двух сигналов, так и для обнаружения общего сигнала в двух различных каналах. Фаза когерентности характеризует отставание или опережение по фазе в канале х по отношению к каналу у как функцию частоты.

На рис. 2 приведен пример взаимного влияния сигналов по соседнему каналу с КАМ-64 с сеткой частот 25 кГц.

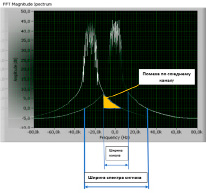
Рис. 2. Пример взаимного влияния сигналов по соседнему каналу с КАМ-64

В таблице приведены данные исследований «наложение спектров сигналов», вызывающее эффект взаимного влияния сигналов.

Заключение

Полученный модифицированный сегментированный метод Прони позволяет определить ширину спектра «перекрытия» соседнего канала связи и вычислить мощность помехи по соседнему каналу. Очень короткий временной ряд обнаружения взаимного влияния сигналов в частотно-фазовом пространстве определяется кодовым словом сигнального созвездия КАМ, что неприемлемо при использовании преобразований Фурье, использующих обобщенный анализ спектральных составляющих на интервале «окна» наблюдения. Разработанный метод позволяет оценить взаимное влияние сигналов как в частотном, так и «фазовом» спектре с использованием коэффициента взаимного влияния сигналов.