Scientific journal

Scientific Review. Technical science

ISSN 2500-0799

ПИ №ФС77-57440

Прогнозирование результатов спортивных событий требует оценки и анализа набора данных, влияющих на итоговый результат. Результатом прогноза являются численный результат или формализованное утверждение о наступлении некоторого исхода спортивного события. Набор данных, влияющих на итоговый результат прогноза, может быть слабо структурирован, иметь сильно отличающиеся по типу и размеру значения.

При прогнозировании с использованием средств машинного обучения такой набор данных называют обучающим набором, или обучающей выборкой [1]. Среди наиболее популярных средств ИИ, применяемых в качестве инструмента прогнозирования, можно выделить генетические алгоритмы, экспертные системы на основе логического вывода [2], математические средства моделирования [3], искусственные нейронные сети [4, 5, 6], в том числе комбинированные решения на основе нейронных сетей [7] – ансамбли нейронных сетей [8].

В данной работе в качестве основного инструмента прогнозирования рассматриваются нейронные сети.

Целью проводимых исследований являются оптимизация и повышение точности процесса прогнозирования в индивидуальных и командных видах спорта.

Материалы и методы исследования

В работах [9, 10] описываются эксперименты по прогнозированию различных спортивных результатов: командных, мультикомандных, индивидуальных – с применением каскада нейросетевых модулей.

При прогнозировании в экспериментах применялись три типа выборок. Обучающая выборка (dataset, выборка) – совокупность данных, обработанная для использования алгоритмами машинного обучения (Machine Learning). Под использованием подразумеваются обучение модели и дальнейшее ее применение для решения реальных задач на основе готового и структурированного набора данных, представленного в табличном виде. Благодаря обучающей выборке реализуются настройка и оптимизация параметров алгоритма, вследствие чего модель обучается. Контрольная (тестовая) выборка не зависит от обучающей выборки и в идеальном варианте должна содержать в себе новые данные. Благодаря этому этапу происходит проверка качества обученной модели. Валидационная выборка также не зависит от обучающей выборки, помогает выбирать наилучшую обученную модель.

Для обучения каскада, предлагаемого авторами, стандартная обучающая выборка прямоугольного вида (двумерный массив) (рис. 1) не может быть использована, поскольку структура каскада предполагает применение ограниченных фрагментов.

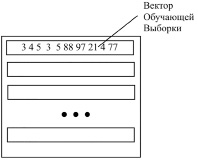
Рис. 1. Обучающая выборка (двумерный массив)

Каждая из строк двумерного массива содержит набор параметров одного «наблюдения» в один временной период. Набору таких параметров соответствует известный элемент, известный в данный момент времени итоговый (профильный) результат.

При формировании фрагментированной структуры обучающей выборки двумерный массив данных разбивается на двумерные массивы меньшей размерности (рис. 2). Основным принципом разбиения является наличие логических зависимостей между элементами выборки, при условии, что элемент изначально не является итоговым результатом.

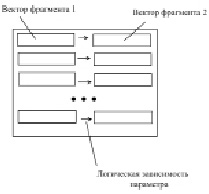
Рис. 2. Разбиение обучающей выборки на два фрагмента

Определение зависимости фрагментов обучающей выборки происходит на основе наличия логической зависимости между отдельным прямоугольным фрагментом и вектором и «столбцом» элементов из связываемого фрагмента. Количество связываемых фрагментов не ограничено. Логические связи могут быть выстроены исходя из предметной области, экспертного мнения или математической связи, выявленной с помощью отдельного блока анализатора.

Фрагменты выстраиваются в логически взаимосвязанную последовательность или последовательности (рис. 3).

Выделяются два типа параметров: предикторы – независимые переменные; целевые признаки – зависимые переменные, вычисляемые на основе предикторов.

Существует первичный набор исходных данных, называемый генеральной совокупностью. В процессе порождения данных из генеральной совокупности формируются выборки. Выборкой является конечное подмножество из элементов генеральной совокупности, проанализировав которое, можно узнать и поведение генеральной совокупности.

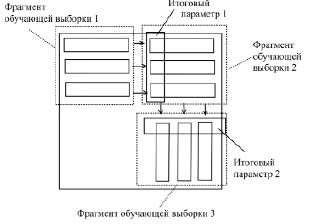
Рис. 3. Разбиение обучающей выборки на три фрагмента

Отдельные из параметров («столбцов») могут оказывать наибольшее влияние на результат или промежуточный результат (итоговый параметр в одном из фрагментов) прогноза. Такие параметры являются прогнозоформирующими предикторами, в работах [10-12] описан алгоритм определения прогнозофорирующих предикторов.

При обучении существующие фрагменты распределяются между выделенными уровнями нейросетевого каскада и являются обучающими выборками для отдельных нейросетевых модулей.

Результаты исследования и их обсуждение

На основе последовательностей определяются уровни нейросетевого каскада. Модули, содержащие сети, распределяются по ярусам каскада. Начиная со второго яруса, на каждый последующий ярус поступают данные промежуточных прогнозов, формирующие следующие прогнозные значения (параметры зависимых фрагментов). Количество прогнозоформирующих предикторов от яруса к ярусу может как уменьшаться, так и увеличиваться. В ряде задач при сокращении размеров обучающей выборки выделение прогнозоформирующих предикторов позволит уменьшить выборку без серьезных потерь в точности результата прогнозирования. Выявление зависимостей по ярусам каскада дает возможность определять те из предикторов, которые наибольшим образом воздействуют на текущие промежуточные результаты на выходе отдельных модулей.

Нейросетевые модули каскада обучаются отдельно, после чего соединяются друг с другом. В качестве эксперимента приведены результаты прогнозирования одного из международных спортивных событий – боксерского поединка. В эксперименте использовалась обучающаяся выборка, сформированная аналогично предыдущему примеру. Однако вектор выборки разбивается на две части. На основе результатов обработки исходных данных первым слоем получаем необходимые элементы выборки, поступающие на второй слой каскада. Нейронная сеть второго слоя обучалась отдельно. Пример разделения параметров во входной выборке и динамического формирования элементов выборок для последующих слоев приведен на рисунке 4.

Для реализации прогноза спроектирован каскад нейросетевых модулей. Каскад состоит из двух обобщенно-регрессионных нейронных сетей во входном (первом) слое и одной LVQ сети в заключительном модуле выходного (второго) слоя каскада [12]. Непосредственно результаты прогнозирования приведены в таблице.

Вектор (0,1) означает победу второго боксера, вектор (1,0) – победу первого боксера. В большинстве экспериментов система верно определила победителя. Определение логических взаимосвязей в обучающей выборке позволяет детализировать прогноз и динамически формировать промежуточные результаты, которые одновременно являются предикторами для последующих уровней каскада.

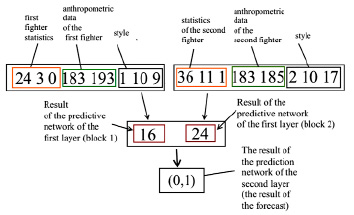
Рис. 4. Пример формирования обучающей выборки

Результат эксперимента

Нейросетевой каскада является «решающей» частью так называемой специализированной системы прогнозирования спортивных результатов. При этом фрагментирование выборки на основе логических зависимостей повышало точность прогнозирования как в мультиспортивных, так и в индивидуальных дисциплинах.

Заключение

Детализация прогноза путем динамического формирования вектора данных для последующих слоев каскада позволяет уменьшить объем информации, обрабатываемый последующими слоями, и увеличить точность прогноза.

Применение нейронных сетей для прогнозирования спортивных результатов в индивидуальных и командных дисциплинах перспективно и эффективно. Построение нейросетевого каскада невозможно без выделения логических взаимосвязей в обучающей выборке. На данный момент тестируется отдельный модуль системы, автоматически определяющий не только прогнозоформирующие предикторы, но и наиболее сильные логические взаимосвязи между фрагментами выборки.

Продолжается тестирование различных вариантов нейросетевого каскада на основе новых вариантов фрагментированных обучающих выборок. Фрагменты обучающих выборок могут быть дополнены уникальными параметрами, которые не содержатся в исходном датасете.

Применение системы на основе нейросетевого каскада в качестве инструмента прогнозирования специалистами сферы физической культуры и спорта позволит повысить точность прогнозов, на основе которых можно выстраивать процесс планирования тренировки и подготовки спортсменов.