science-review.ru
Криптографическим преобразованием информации (далее – КПИ) называется процесс изменения информации, зависящий от изменяемого параметра и обладающий свойством невозможности восстановления исходной информации по преобразованной, без знания действующего ключа, с трудоемкостью меньше заданной [1].
В настоящее время КПИ осуществляется программными, аппаратными и программно-аппаратными средствами. При этом в случае даже минимальной ошибки в 1 бит процесс восстановления информации становится невозможным.
Особенно актуальна проблема возникновения ошибки в ходе КПИ на автономных технических средствах (далее – АТС), осуществляющих работу на большом расстоянии от технического оператора и передающих криптографически преобразованную информацию на объект обработки по радиоканалам [2].
В связи с этим возникает необходимость автономного контроля выполнения КПИ на АТС для заблаговременного определения ошибки и, по возможности, устранения сбоя в работе устройства, осуществляющего КПИ.
Основным вычислительным устройством, выполняющим КПИ, в настоящее время служит программируемая логическая интегральная схема. Данное вычислительное средство является наиболее универсальным для реализации различных алгоритмов КПИ.
В основе наиболее криптостойких алгоритмов лежат четыре основные логические операции [3]:
- операция сложения по модулю 2;
- операция сложения по модулю 216;
- операция циклического сдвига;
- операция подстановки.
Контроль данных логических операций позволит наиболее полно определять техническое состояние ПЛИС, осуществляемой КПИ на АТС.
Рассмотрим числовой контроль логических операций. В основе построения схем контроля лежат две теоремы [4, 5].
Теорема 1. Сумма чисел сравнима по модулю q с суммой остатков r этих же чисел, то есть:
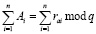(1)
Теорема 2. Произведение чисел сравнимо по модулю q с произведением остатков r этих же чисел, то есть:
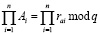(2)
Рассмотрим схему контроля для логической операции сложения по модулю 2.
Схема контроля преобразования [6] (суммирования) двух чисел A1 и A2 по модулю два представлена на рисунке 1.
Поясним работу данной схемы следующим образом [7, 8]. Результатом суммирования двух чисел A1 и A2 есть число A3. В блоках B1 и B2 осуществляется вычисление остатков r1 и r2 чисел A1 и A2 до преобразования соответственно. Далее в блоке S происходит суммирование полученных остатков. Поскольку сумма остатков может быть больше модуля, то на выходе сумматора необходимо еще раз выполнить операцию нахождения остатка с помощью преобразования в блоке B3. В результате выполняется сравнение остатка r3, полученного от числа A3, с суммой остатков чисел A1 и A2 – r∑ с формированием признака «норма» (Р) в виде логической единицы и нуля в противном случае.
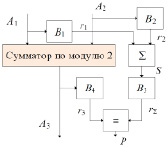
Рис. 1. Схема контроля суммирования по модулю 2
Алгоритм функционирования схемы контроля операции сложения по модулю 2 представлен на рисунке 2.
Условно работу данного алгоритма можно разбить на несколько этапов.
1. На начальном этапе осуществляются получение чисел A1 и A2, участвующих в операции сложения по модулю 2, а также получение остатков r1 и r2 из данных чисел.
2. На следующем этапе выполняются операция сложения по модулю 2 чисел A1 и A2 (получение числа A3), а также суммирование остатков r1 и r2 (S = r1 + r2).
3. На третьем этапе осуществляется поиск остатков от результата суммирования S и A3.
4. На заключительном этапе осуществляется сравнение остатков от суммы чисел A1 и A2 (числа A3) и суммы остатков r1 и r2 (S).
С формальной точки зрения данные этапы могут быть представлены совокупностью отображений:
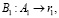(3)
где B1 – оператор, характеризующий процедуру получения остатка r1 от числа A1;
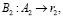(4)
где B2 – оператор, характеризующий процедуру получения остатка r2 от числа A2;
Необходимо отметить, что выражения (3) и (4) являются эквивалентными по функциональному представлению операторов B1 и B2.
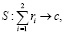(5)
где S – оператор, формализующий нахождение суммы остатков слагаемых r1 и r2, полученных в результате отображений (3) и (4);
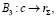(6)
где B3 – оператор, характеризующий процедуру получения остатка r∑ от суммы остатков r1 и r2;
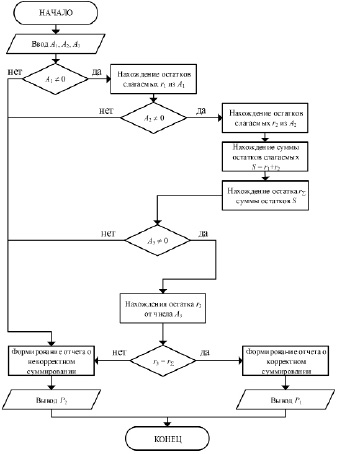
Рис. 2. Алгоритм выполнения контроля операции сложения по модулю 2
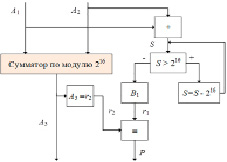
Рис. 3. Схема контроля суммирования по модулю 216
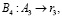(7)
где B4 – оператор, характеризующий процедуру получения остатка r3 от суммы чисел A1 и A2 (числа A3);
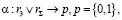(8)
где α – оператор, формализующий процедуру сравнения r3 и r∑.
При контроле сложения по модулю 216 схема упрощается (рис. 3) с учетом того, что вычисляется остаток двух чисел в самом преобразовании.Необходимо отметить, что в данном случае результатом выполнения суммирования по модулю 216 является получение непосредственно остатков чисел, что с практической точки зрения позволяет упростить реализацию процесса контроля. В свою очередь, формирование признака осуществляется аналогично описанному выше случаю.
Алгоритм функционирования представленной схемы контроля представлен на рисунке 4.
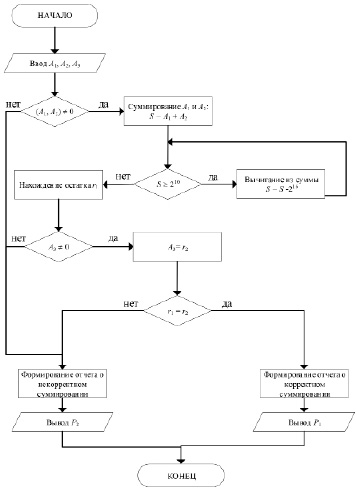
Рис. 4. Схема выполнения контроля операции сложения по модулю 216
Условно работу представленного алгоритма также можно разбить на несколько аналогичных этапов, представленных ранее. Отличие в данном случае заключается в отсутствии процедуры нахождения остатков при реализации отображений (3) и (4).
Следующим основным преобразованием, участвующим в алгоритмах КПИ, является операция сдвига. На рисунке 5 представлена обобщенная схема операции циклического сдвига.
Работу данной схемы можно описать следующим образом. Результатом сдвига числа A1 есть число A2. Для блоков B1 и B2 осуществляется разделение битовой последовательности двоичного представления числа A1 на два блока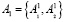 
, которые в ходе выполнения операции будут переставлены относительно старшего и младшего разрядов (рис. 6).
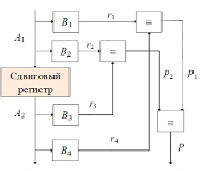
Рис. 5. Схема выполнения контроля операции сдвига
Поясним отдельно данное утверждение: в блоке B1 преобразуется в остаток r1 та часть двоичной последовательности (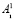
), которая в дальнейшем будет участвовать в операции сдвига и в полном объеме будет смещена циклически в сторону младшего разряда; в свою очередь в блоке B2 преобразуется в остаток r2 та часть двоичной последовательности (
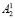), которая будет смещена в сторону старшего разряда и будет переписана на месте двоичной последовательности числа 
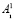. Далее в блоке сдвигового регистра происходит выполнение операции сдвига, в результате которой появляется число A2. Поскольку сдвиг является циклическим, смещенные биты не исчезают, а заполняют освободившиеся разряды с противоположной стороны битовой последовательности.
Исходя из этого, разделив битовую последовательность двоичного представления числа A2 на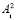 
и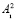 
, возможно осуществить контроль правильности выполнения операции сдвига следующим образом. В блок B3 (формирование остатка r3) необходимо записать количество разрядов, равное количеству разрядов для блока B2. Аналогично заполняется блок B4 (формирование остатка r4). После выполнения операции сдвига, сравнив остатки r1, r4 и r2, r3 блоков B1, B2, B3 и B4, можно сделать вывод о правильности выполнения циклического сдвига, тем самым осуществив контроль правильности выполнения операции. Необходимо отметить, что в блоках сравнения сопоставляются не целые значения чисел, а их остатки, что повышает скорость процесса сравнения сколь угодно больших блоков информации.
Алгоритм функционирования представленной схемы контроля представлен на рисунке 7. Работа представленного алгоритма может быть разбита на несколько этапов.
1. На начальном этапе осуществляются получение чисел A1 и A2, участвующих в операции сдвига, а также разбиение числа A1 на два блока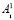 
и 
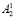битовой последовательности. Также на данном этапе происходит нахождение остатков r1 и r2 в блоках B1 и B2 соответственно.
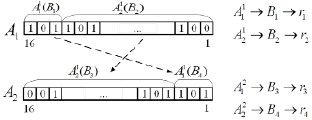
Рис. 6. Сдвиг в сторону старшего разряда на 3
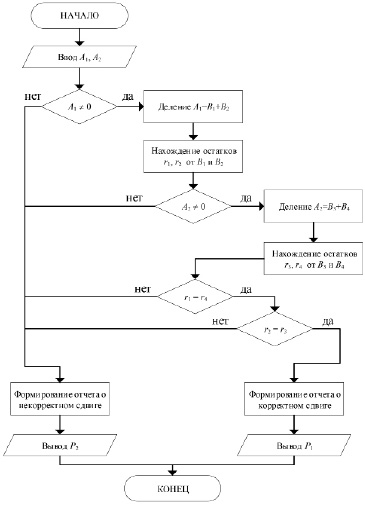
Рис. 7. Алгоритм выполнения контроля операции сдвига
2. Аналогично на следующем этапе осуществляются разбиение числа A2 на два блока B3 и B4 битовой последовательности и нахождение остатков r3 и r4 от блоков B3 и B4 соответственно.
3. На заключительном этапе осуществляются сравнение остатков r1 и r4 от блоков битовой последовательности B1 и B4, остатков r2 и r3 от блоков B2 и B3, а также формирование отчета о корректном или некорректном сдвиге (вывод P1 и P2 соответственно).
Представим данные этапы в виде совокупности отображений:
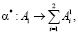(9)
где α* – оператор, характеризующий процедуру разбиения числа A1 на битовые последовательност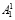и 
и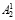 
соответственно;
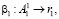(10)
где β1 – оператор, характеризующий процедуру получения остатка r1 от битовой последовательности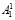 
в блоке B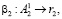1;
(11)
где β2 – оператор, характеризующий процедуру получения остатка r2 от битовой последовательности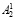 
в блоке B2.
Необходимо отметить, что отображения β3 и β4 имеют схожую интерпретацию для остатков r3 и r4.
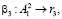(12)
где β3 – оператор, характеризующий процедуру получения остатка r3 от битовой последовательности A1 в блоке B3;
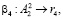(13)
где β4 – оператор, характеризующий процедуру получения остатка r4 от битовой последовательности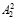 
в блоке B4;
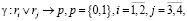(14)
где γ – оператор, формализующий процедуру сравнения r1, r4 и r2, r3 и принятие решения о корректном или некорректном сдвиге.
Последним рассматриваемым преобразованием является операция подстановки. Она заключается в том, что входная последовательность из n-ого количества бит разделяется на два блока с указанным количеством бит, эти блоки определяют адрес ячейки из таблицы замен, в которой записано значение, которое и будет являться результатом подстановки. Но с целью повышения криптостойкости в данном преобразовании применяется также и операция циклического сдвига выходной последовательности. Обобщенная схема контроля правильности выполнения данного преобразования представлена на рисунке 8.
Описание функционирования данной схемы выглядит следующим образом. Поступающее число A1, проходя через блок подстановки N, преобразуется в число A2, которое и является результатом выполнения операции подстановки. Число A1 разбивается на два числа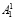 
и 
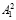, после чего они параллельно поступают в блок подстановки N и блок n. Блок n является таблицей остатков таблицы замены (блока N). Тем самым результат, полученный в ходе выполнения операции подстановки на выходе из блока n, будет представлен в остаточных классах. После этого над полученным результатом проводится операция циклического сдвига со сменой местами блоков двоичной записи результата.
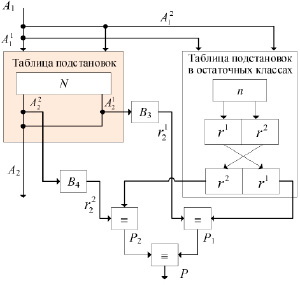
Рис. 8. Схема выполнения контроля операции подстановки
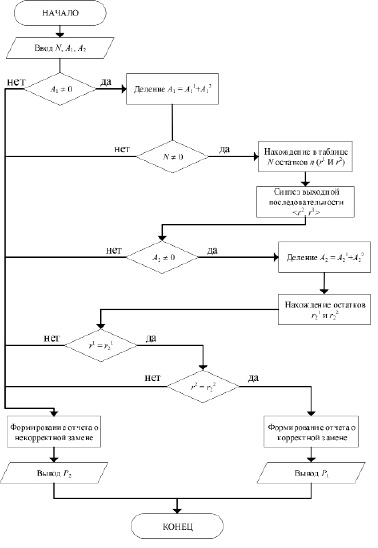
Рис. 9. Алгоритм выполнения контроля операции подстановки
Результатом прохождения чисел А11 и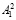 
через таблицу подстановок в остаточных классах n являются числа (остатки) r1 и r2 соответственно. После операции подстановки над блоками r1 и r2 выполняется операция циклического сдвига со сменой их местами. С целью контроля правильности выполнения преобразования подстановки число A2 делят на блок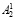и 
и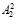 
. Далее в блоках B3 и B4 вычисляются числа (остатки) 
, 
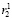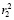битовых последовательносте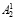й 
и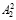 
, записанных в соответствующие блоки. Сравнение остатков r1 и r2, 
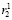и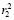 
в блоках сравнения (≡) с формированием результатов P1 и P2 и Р является результатом контроля правильности выполнения операции подстановки. В случае когда в результате сравнения получается, что r1 = 
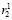и r2 =
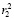, формируется отчет о правильности выполнения подстановки. В случае когда одно из равенств не выполняется либо не выполняются оба неравенства (r1 ≠ 
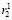, r2 ≠ 
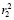), следует вывод о неправильном выполнении контролируемого преобразования.
Алгоритм функционирования данной схемы контроля представлен на рисунке 9.
Работа представленного алгоритма может быть разбита на несколько этапов.
1. На первом этапе осуществляется ввод чисел A1, A2 и таблица замен N. Затем A1 делится на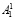 
и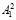 
. После этого находится таблица остатков n из таблицы замен N и находится выходная последовательность, представленная остатками r1 и r2.
2. Второй этап начинается с разделения числа A2 на блок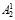и 
и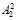 
таким образом, чтобы количество бит в блоках было равно количеству бит в блоках 
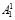и 
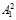соответственно. Далее из блоков 
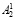и 
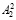формируются остатк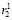и 
и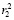 
.
3. На заключительном этапе остатки r1 и r2 сравниваются с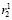 
и 
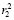, после чего, если равенство выполняется для обоих выражений, формируется отчет о правильности выполнения операции P1, в противном случае формируется отчет о некорректном выполнении операции подстановки P2.
С формальной точки зрения данные этапы могут быть представлены совокупностью отображений:
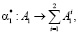(15)
где α1*– оператор, характеризующий процедуру разбиения числа A1 на битовые последовательност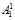и 
и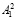 
соответственно;
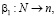(16)
где β1 – оператор, характеризующий процедуру получения таблицы остатков n от таблицы замен N;
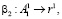(17)
где β2 – оператор, характеризующий процедуру получения значения r1 из таблицы остатков n от входной битовой последовательности А11 ;
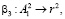(18)
где β3 – оператор, характеризующий процедуру получения значения r2 из таблицы остатков n от входной битовой последовательности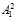 
;
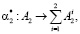(19)
где α2* – оператор, характеризующий процедуру разбиения числа A2 на битовые последовательност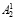и 
и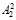 
соответственно;
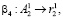(20)
где β4 – оператор, характеризующий процедуру получения значения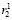 
из битовой последовательности 
;
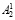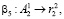(21)
где β5 – оператор, характеризующий процедуру получения значения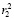 
и битовой последовательности 
;
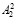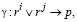
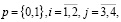(22)
где γ – оператор, формализующий процедуру сравнения r1 и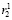 
, r2 и 
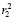, а также принятие решения о корректном или некорректном сдвиге.
Заключение
В ходе исследований были разработаны алгоритмы контроля основных операций алгоритма криптографического преобразования информации на основе модулярной арифметики и в соответствии с предложенными схемами контроля. Указанные алгоритмы лежат в основе формирования общего алгоритма технического диагностирования программируемых логических интегральных схем на автономных технических средствах.