science-review.ru
Одной из основных задач электродинамики является задача расчета параметров излучающих систем различной конфигурации, решаемая ввиду сложности зачастую численными методами [1, 2]. Задача излучения точечными зарядами является базовой моделью для исследования излучающих систем различного типа [2, 3]. Решения в виде аналитических соотношений, наиболее удобных для анализа физических свойств излучающих структур, ранее были получены только для простейших конфигураций: излучение точечных источников и излучение моделей бесконечно длинных заряженных стержней при однородном распределении линейной плотности заряда по длине проводника [4, 5]. Возможность получения аналитических решений при расчете полей различных конфигураций излучателей показана в [6]. Для реальных, но более сложных конфигураций используются численные методы расчета, что существенно затрудняет анализ и исследование физических свойств этих структур и проектирование излучающих антенных систем на их основе. Вопрос о необходимости учета неоднородности распределения линейной плотности заряда для корректного расчета излучаемых полей ставился в [7]. В настоящей работе показана возможность аналитического решения задачи расчета электростатического поля, создаваемого заряженным стержнем конечной длины с неоднородным распределением линейной плотности заряда по длине проводника. Получены аналитические соотношения для расчета компонент напряженности и потенциала электростатического поля заряженного стержня для некоторых функций, описывающих неоднородность распределения линейной плотности заряда по оси стержня, переходящие в пределе в известные соотношения для заряженного стержня неограниченных размеров и для точечного заряда. Рассмотрена структура поля в области заряженного стержня и ее зависимость от распределения линейной плотности заряда на стержне.
Целью работы являлось аналитическое решение задачи расчета электростатического поля заряженного стержня с неоднородным распределением плотности заряда по длине стержня, получение обобщения ранее известных аналитических соотношений для расчета компонент напряженности электростатического поля для неоднородного распределения линейной плотности заряда по стержню, численное исследование структуры электростатического поля, создаваемого заряженным стержнем.
Материалы и методы исследования
Для исследования использовались уравнения классической электростатики для расчета полей стержней ограниченных в пространстве размеров. Получено графическое представление поля излучения в пространстве.
Результаты исследования и их обсуждение
Рассмотрим тонкий заряженный стержень с плотностью распределения зарядов, вдоль оси стержня, описываемой в общем случае функцией τ(x) (рис. 1). Проведем расчет поля в произвольной точке А, положение которой определяется расстоянием r0 от оси стержня и углами β1, β2, под которыми видны концы стержня из точки наблюдения. Из рисунка следует, что соотношения между геометрическими параметрами имеют вид
, 
.
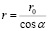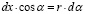Компоненты напряженности электростатического поля, создаваемого каждым элементом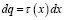 
заряженного стержня (рис. 1) под углом α, определяются соотношениями
,
.
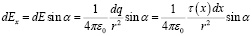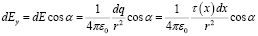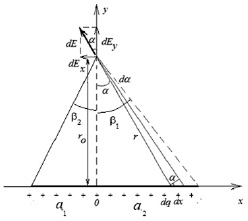
Рис. 1. К расчету электростатического поля, создаваемого заряженным стержнем, расположенным вдоль оси 0x в области (–a1,a2 )
Тогда x и y компоненты поля
,
.
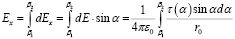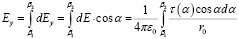Потенциал электростатического поля, создаваемого стержнем в той же точке:
.
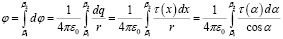В частном случае однородного распределения линейной плотности заряда вдоль оси стержня (τ(x) = сonst) имеем для компонент напряженности поля соотношения
,
,
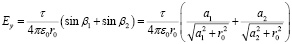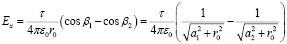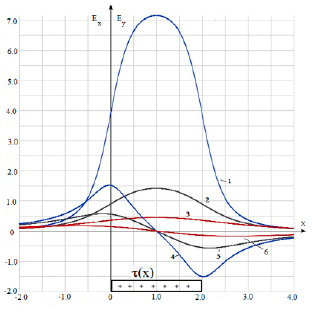
Рис. 2. Изменение нормированных на kτ (k = 9 ? 109) компонент напряженности электрического поля (Ex (кривые 4, 5, 6), Ey ( кривые 1, 2, 3) вдоль оси заряженного стержня с линейной плотностью распределения заряда τ = сonst, l = 2 , a1 = 0, кривые 1, 4 – r0 = 0,5, кривые 2, 5 – r0 =1, кривые 3, 6 r0 =2)
и для потенциала: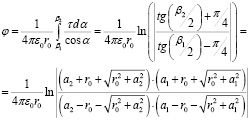 
.
Характер изменения компонент поля вдоль осей, параллельных оси стержня вблизи стержня, показан на рис. 2.
Характер изменения поля при разном удалении от стержня сохраняется, уменьшаясь по величине.
Изменения компонент поля при удалении точки наблюдения в направлении, перпендикулярном оси стержня, у одного из концов стержня показан на рис. 3, уменьшаясь по величине.
Наблюдается рост Ey компоненты поля при приближении к центральной части стержня. В центральной части стержня по оси перпендикулярной стержню компонента электростатического поля Ex = 0 при этом на любом расстоянии от стержня. На больших расстояниях от стержня (при r0 >> a1, a2), когда заряженный стержень можно считать точечным источником, расчетное соотношение для компонент напряженности электрического поля принимает известный вид
, 
, 
.
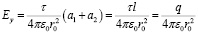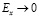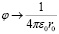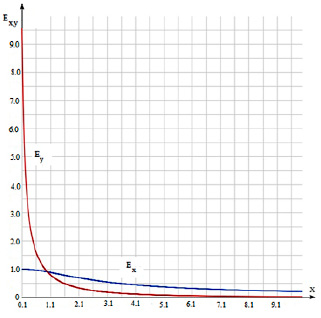
Рис. 3. Зависимость нормированных на kτ компонент поля от расстояния до стержня (длина стержня l = 2, x = r0/l, a1 = 0, a2 = l)
В случае неоднородного распределения линейной плотности заряда вдоль оси стержня, описываемого функцией τ = χα, компоненты поля определяются соотношениями
,
.
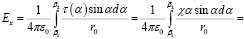
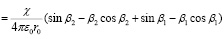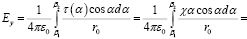
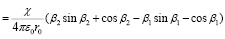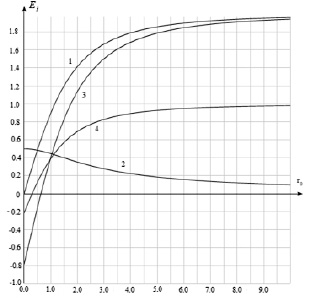
Рис. 4. Зависимость нормированных на kτ ( кривые 1, 2) и на kχ компонент Ex, Ey поля от расстояния до стержня при однородной (1, 2) и неоднородной (3, 4) линейной плотности распределения зарядов (здесь кривые 1, 4 – Ey – компоненты поля, кривые 2, 3 – Ex – компоненты поля)
На рис. 4 показана зависимость перпендикулярной и касательной к оси стержня компонент напряженности электростатического поля в зависимости от расстояния от оси стержня при однородном и неоднородном, описываемой линейной функцией, распределениях линейной плотности заряда. Изменение распределения линейной плотности заряда существенно влияет на структуру электрического поля – меняет не только величину, но и направление поля вблизи заряженного стержня. При этом нормированная перпендикулярная к оси стержня компонента поля при удалении от стержня имеет одинаковый характер изменения и различается при приближении с стержню, касательная составляющая поля (рис. 1) меняет характер изменения (вместо убывания величины компоненты поля при однородном распределении заряда – величина поля возрастает).
В случае другого типа неоднородного распределения линейной плотности заряда, описываемого квадратичной функцией распределения, τ = χ2α2 компоненты поля определяются соотношениями
,
.
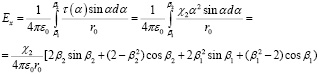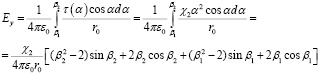Неоднородность распределения плотности заряда приводит к существенному изменению структуры поля вблизи концов заряженного стержня, что необходимо учитывать при расчете реальных структур. Таким образом, используемая во многих работах модель однородной плотности распределения не отражает реальной ситуации. Полученные в данной работе результаты позволяют обобщить ранее известные результаты и провести их коррекцию.
Заключение
Рассмотрена зависимость структуры электростатического поля, создаваемого заряженным стержнем конечной длины в зависимости от распределения линейной плотности заряда. Получены аналитические соотношения для расчета компонент вектора напряженности электрического поля при однородном и неоднородном распределении линейной плотности заряда вдоль заряженного стержня. Полученные соотношения обобщают известные соотношения для предельного случая бесконечно длинного стержня с однородным распределением линейной плотности заряда. Распределение заряда влияет на характер поля вблизи источника поля, что может быть использовано для исследования распределения зарядов путем измерения структуры распределения полей в области источников поля.