science-review.ru
При наложении волн, создаваемых когерентными источниками, возникает эффект интерференции, широко используемый на практике для создания различных оптических, акустических, радио- и квантовых устройств, таких как интерференционные фильтры, спектроскопы, интерферометры и др. Эти устройства используются во многих областях науки и техники, включая оптику, электронику, устройства телекоммуникаций, медицину. Интерференция, возникающая при наложении волн, излучаемых когерентными осцилляторами, сравнительно хорошо изучена. Наиболее простой моделью интерференции от излучения двух когерентных источников оптического диапазона длин электромагнитных волн является известный опыт Юнга [1], который имеет аналоги и для других типов волновых процессов. В многочисленных работах, посвященных исследованию явления интерференции, основное внимание уделяется удаленным фотонным когерентным системам передачи информации [2-4] многолучевой интерференции когерентных излучателей [5], влиянию интерференции на передачу сигналов по линиям связи [6], влиянию на интерференцию поляризации [7], временной интерференции [8; 9], вопросам взаимодействия когерентных и квазикогерентных осцилляторов [10]. Вопросы нарушения когерентности излучения и временные аналоги опыта интерференции на двух щелях рассматривались в [9; 10]. В настоящей работе установлено, что отклонение частот излучения осцилляторов от точной когерентности приводит к качественному изменению картины интерференции– статическое распределение интенсивности меняется на динамическое, и в каждой точке пространства возникает биение интенсивности результирующего излучения с частотой, определяемой величиной сдвига частот осцилляторов. Рассмотрена интерференционная картина, формируемая квазикогерентными осцилляторами для различных положений осцилляторов.
Целью исследования являлся анализ изменения физических свойств системы при малом нарушении когерентности излучения двух точечных осцилляторов, получение аналитических решений для расчета распределения интенсивности излучения и сопоставление с картиной интерференции, создаваемой системой когерентных осцилляторов.
Материалы и методы исследования
Рассматривается суперпозиция электромагнитных волн, создаваемых системой квазикогерентных осцилляторов, получены аналитические соотношения для расчета интенсивности излучения системы квазикогерентных осцилляторов в зависимости от разности частот излучения. Представлены графики полученной картины интерференции пространственного распределения излучения при некогерентности излучения осцилляторов.
Базовые соотношения
Для простоты физической модели сцелью получения аналитического решения рассмотрим два осциллятора с различными (но близкими) частотами осцилляции. В соответствии с принципом суперпозиции результирующее поле в произвольной точке P пространства (рис. 1) можно представить в виде:
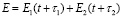, (1)
где τ1, τ2– время запаздывания колебаний в точке наблюдения Р (рис. 1) от колебаний, создаваемых в момент времени t осцилляторами, расположенными в точках с координатами: x = 0, y = d и x = 0, y = -d.
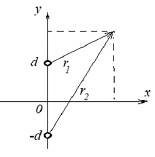
Рис. 1. Конфигурация двух квазикогерентных осцилляторов
Расстояния от каждого осциллятора до точки наблюдения определяются в соответствии с рисунком 1 соотношениями:
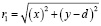
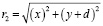
Каждое из двух однонаправленных колебаний описывается функцией:
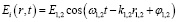, (2)
где Е1,2– амплитуды,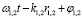 
– фазы колебаний, создаваемых осцилляторами в точке наблюдения Р, частоты осцилляторов в общем случае различаютсяω1 ≠ ω2, при этом для квазикогерентных колебаний двух источников ω1 ≈ ω2, k1,2– волновые векторы. Для простоты полагаем φ1,2 = 0 и амплитуды осцилляторов одинаковыми. Обобщение на случай большего числа осцилляторов проводится аналогично [5].
Результаты исследования и их обсуждение
В частном случае одиночного излучателя из (1) следует, что распределение интенсивности волн стабильно во времени и имеет равномерное распределение в пространстве. Для двух квазикогерентных источников имеем соотношение:
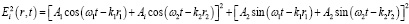,(3)
где частоты квазикогерентных колебаний различаются и соответственно равны:
,
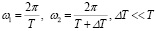волновые числа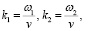 
v– скорость распространения волн.
В рассматриваемом случае амплитуда результирующего колебания зависит не только от положения точки наблюдения в пространстве (как в стабилизированной картине распределения энергии при интерференции волн когерентных источников), но и от времени t. Соотношение (3) представим в другом виде, более удобном для аналитического исследования картины интерференции. Сложение колебаний (3) дает соотношение:
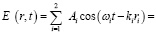
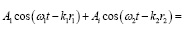
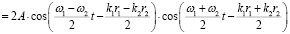(4)
Из которого следует, что в частном случае когерентных источников (ω1 = ω2) амплитуда результирующего поля зависит только отположения точки наблюдения в пространстве: от параметра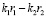 
, и не зависит от времени. В случае же некогерентных источников ω1 ≠ ω2 и амплитуда 
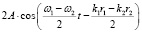зависит не только от положения точки наблюдения в пространстве, но и меняется со временем с частотой Δω/2, определяемой расстройкой частот осцилляции. В каждой точке пространства наблюдается биение интенсивности. На рисунке 2а показано распределение интенсивности картины интерференции двух когерентных источников, и для сравнения на рисунке 2б показано распределение интенсивности тех же источников при нарушении когерентности излучения этих осцилляторов (для Δω ≈ 0.1ω). Осцилляторы расположены на расстоянии длины волны. Нарушение когерентности меняет структуру поля.
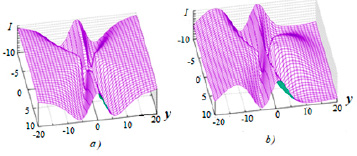
Рис. 2. Интерференция когерентных (a) и квазикогерентных (b) источников, расположенных на расстоянии d = λ
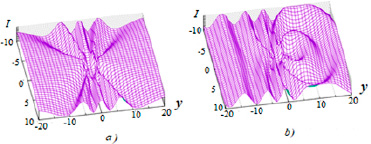
Рис. 3. Интерференция когерентных (a) и квазикогерентных (b) источников излучения, расположенных на расстоянии d = 2λ
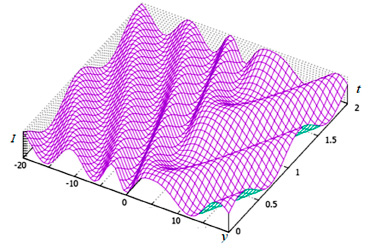
Рис. 4. Изменение со временем интерференционного распределения интенсивности излучения некогерентных осцилляторов на экране, расположенном по оси Оy в плоскости x = 5
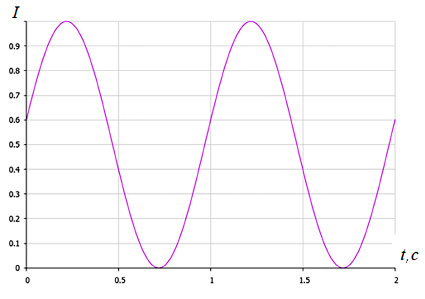
Рис. 5. Зависимость интенсивности излучения от времени
На рисунке 3а показано распределение интенсивности излучения картины интерференции двух когерентных источников, и для сравнения на рисунке 3б показано распределение интенсивности тех же источников при таком же нарушении когерентности для источников, расположенных на расстоянии d = 2λ. При удалении осцилляторов друг от друга наблюдается более значительная деформация картины интерференции.
На рисунке 4 показано изменение со временем картины интерференционного распределения интенсивности излучения двух некогерентных осцилляторов на проекционном экране, расположенном на расстоянии х = 5 см от линии, проходящей через заряды. С течением времени интерференционная картина смещается со скоростью, пропорциональной разности частот осцилляторов.
На рисунке 5 показана зависимость изменения интенсивности излучения двух осцилляторов от времени, наблюдающаяся в каждой точке пространства.
Из рисунков 2 и 3 видно, что для всех точек пространства, расположенных на оси Оx, перпендикулярной к линии расположения излучателей, амплитуда колебаний максимальна и постоянна для всех точек, относительно которых осцилляторы расположены симметрично (для которых выполняется соотношение: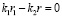 
). Вдругих точках пространства амплитуда, наоборот, пульсирует с частотой Δω и периодом T = 2π / Δω. Период пульсаций растет с уменьшением разности частот осцилляторов. Пульсации исчезают для когерентных осцилляторов (T → ∞ при Δω → 0).
Заключение
Рассмотрено изменение интерференционной картины при нарушении когерентности частот излучения осцилляторов, расположенных в изотропной однородной среде. Установлено, что отклонение от когерентности излучения приводит к нарушению симметрии интерференционной картины относительно осцилляторов: область минимумов интенсивности излучения смещается в сторону осциллятора с наименьшей частотой излучения. Кроме того, уменьшается длина волны, формируемой между осцилляторами. Это приводит к формированию воздействия на осцилляторы: на осцилляторы с более высокой частотой осцилляции действуют силы в направлении осцилляторов с низкой частотой осцилляции. Нарушение когерентности приводит к неустойчивости системы свободных осцилляторов, к возникновению зависимости результирующей амплитуды колебаний не только от положения точки наблюдения, но и от времени. Возникает пульсация величины интенсивности излучения во всех точках пространства с частотой, равной разности частот излучателей. Показана зависимость интерференционной картины от величины разности частот излучения квазикогерентных излучателей и их взаимного положения в пространстве.