Для измерения скорости движения тел часто используется физический эффект изменения частоты излучения волн между взаимодействующими объектами при их взаимном перемещении, известный как эффект Доплера, получивший широкое применение в технике [1–3]. Этот способ косвенных измерений часто является единственным для измерений скорости движения объектов любой природы в том случае, когда прямые измерения становятся недоступны [4–6]. Он также лежит в основе построения большого числа современных теорий о физике различных природных процессов, в том числе и о структуре Вселенной [4]. Известны и экспериментально зафиксированы многочисленные разновидности эффекта Доплера, в том числе: аномальный, обратный, двойной, угловой, вращательный, мультимодовый [7, 8], в киральных, нелинейных [9], метасредах, в акустооптике, магнитооптике, плазмонике и др. Эти разновидности эффекта Доплера значительно расширяют возможности его практического использования в различных диапазонах частот (оптическом, микроволновом) с применением волн различной физической природы (упругих, электромагнитных и др.). Следует отметить, что на практике, в технике измерений эффект Доплера может быть использован обычно в ограниченные и сравнительно кратковременные промежутки времени работы измерительных приборов. При этом выполняются условия равномерного друг относительно друга перемещения источника излучения и приемника волн или волн отраженных от равномерно движущейся границы раздела сред. В то же время известно, что часто при измерениях, например, в задачах радиолокации всегда имеет место неравномерность движения взаимодействующих объектов, получившее название эффекта микро-Доплера [7]. В этих условиях характеристики эффекта существенно меняются, и учет неравномерности движения является важной для практики задачей. Для теоретического описания и анализа эффекта Доплера обычно используются достаточно наглядные геометрические модели [1, 2], которые позволяют провести анализ сравнительно простых ситуаций. В то же время для решения более широкого круга задач может быть использована менее разработанная волновая теория [1, 4, 8]. Задача отражения волн от подвижных границ рассматривалась авторами [10, 11] без учета всех параметров граничащих сред, которые, как показывает анализ, могут существенно влиять на параметры эффекта. Отметим, что движение сред увлекает волновые процессы в этих средах, что приводит к изменению скорости волн в этих средах и анизотропии параметров. На отражение волн влияют как движение и характер этого движения (равномерное или неравномерное движение) границ раздела сред, так и скорости перемещения самих волноведущих сред, примыкающих к границе. Установлено, что помимо эффекта Доплера при неравномерном движении границы наблюдается дополнительный нестационарный во времени сдвиг частоты, определяемый величиной ускорения. В аналитическом виде получено решение задачи о нахождении частот отраженных и прошедших через границу раздела волн с неравномерно движущимися границами также подвижных сред. Было также установлено, что учет только доплеровского смещения частоты в некоторых случаях приводит к большим ошибкам измерения скорости объектов. Показано, что смещение частоты отраженных волн от ускоренно движущейся границы раздела сред может наблюдаться и в отсутствие эффекта Доплера и в определенных условиях превышать смещение частоты, наблюдаемого за счет классического эффекта Доплера.
Материалы и методы исследования
Методами электродинамики была рассмотрена задача анализа отражения и прохождения волн от неравномерно движущейся границы раздела двух различных сред, каждая из которых (для общности) также может перемещаться. Рассмотрим движение границы в направлении оси 0z (рис. 1). Для постоянной скорости [1, 8, 10] ее координата описывается в виде функции z(t) = ut, что соответствует условиям выполнения эффекта Доплера [2]. При равнопеременном движении границы ее координата описывается функцией
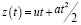 . (1)
. (1)
Отметим, что зависимость изменения частоты движущимся источником излучения от величины ускорения для задачи ускоренного сближения источника и приемника рассматривалась для другой конфигурации Ритцем, который обнаружил ее отличие от эффекта Доплера [12]. Эти эффекты не зависят от физической природы волнового процесса.
Граница разделяет две среды, характеризуемые параметрами ε1, μ1 и скоростью распространения волн с1 в первой среде и ε2, μ2, с2 во второй среде. Каждая среда может перемещаться самостоятельно или вместе с границей раздела вдоль оси 0z со скоростью υ1 и υ2 соответственно. Движение сред приводит к увлечению волнового процесса в каждой из этих средах, тогда и результирующие скорости распространения волн в средах меняются: вдоль оси 0z скорость прямых волн в первой среде равна с10 = с1 + υ1, скорость распространения обратных волн с1R = с1 – υ1. Во второй среде в рамках полубезграничной среды волны, прошедшие через границу раздела сред, распространяются вдоль оси 0z со скоростью с2T = с2 – υ2. Функции тангенциальных к границе раздела компонент напряженности электрического поля падающей E10, отраженной E1R и прошедшей E2T волн удовлетворяют волновым уравнениям для электромагнитных волн в этих средах. Граничные условия непрерывности y-компоненты волны Ey, Hx, Hz имеют вид [13, 14]:
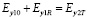 . (2)
. (2)
Решение волновых уравнений в первой и второй средах ищутся в виде волн
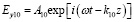 ,
,
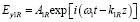 , (3)
, (3)
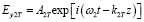 .
.
где выбраны различные частоты для прямой ω, обратной ω1 и прошедшей ω2 волн в соответствии с эффектом изменения частоты волн при взаимодействии с движущейся границей раздела сред (эффектом Доплера).
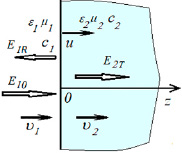
Рис. 1. Падение волны на подвижную границу раздела сред
Волновые числа для каждой из этих волн определяются соответственно соотношениями
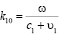 ;
; 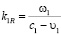 ;
; 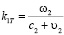 .
.
Поиск решений волновых уравнений в виде (3) дает возможность получить аналитическое решение задачи прохождения волны через движущуюся границу раздела, удовлетворяющее и волновым уравнениям в каждой среде, и граничным условиям (2). Отметим, что прошедшие волны, как и отраженные также при некоторых условиях могут изменить частоту, что ранее в литературе не рассматривалось, поскольку это условие возникает только при различии параметров первой c1 и второй c2 сред (c1 ≠ c2).
Результаты исследования и их обсуждение
Учет граничных условий дает соотношение
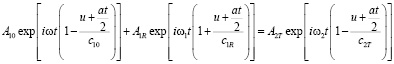 ,
,
которое должно выполняться в любой момент времени t, что приводит к необходимости выполнения соотношений меду фазами
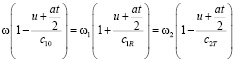 . (4)
. (4)
Полученное соотношение показывает связь частот волн, падающей на границу раздела сред ω, отраженной от границы ω1 и прошедшей ω2 волн. В отличие от известных результатов [1] здесь появляется зависимость частот отраженной и прошедшей волн дополнительно от ускорения и от времени. Соотношения (4) переходят в формулы для эффекта Доплера при u = const (a = 0). Отметим, что это приближение часто выполняется на практике и может быть использовано и при неравномерном движении тел в промежутки времени, когда выполняется условие at < < u,c (которое, однако, с течением времени нарушается). В этом случае параметр at растет и основным в соответствии с (4) становится именно эффект изменения частоты, связанный с ускорением. Отметим, что этот эффект существует и в более общем случае для переменного ускорения, который требует отдельного анализа. Отметим, что эффект Доплера и эффект Ритца (изменение частоты обратной волны) существуют при условии существования обратной волны. Поэтому для наблюдения эффекта Доплера необходимо обеспечить выполнение условия c1 + υ1 > u при движении первой среды или (если эта среда неподвижна и υ1 = 0), c1 > u. Эффект Ритца существует при выполнении более общего соотношения:
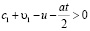 .
.
В случае, если выполняется условие:
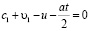
или становится отрицательным, то волна в первой среде, движущаяся в направлении границы раздела сред, не догоняет движущуюся границу раздела сред и эффект сдвига частоты отраженной волны и сама отраженная волна не формируются. Этот же случай наблюдается и при выполнении соотношения: c1 = υ1 (в тот момент, когда скорость движения среды совпадает скорости распространения волн). В этих случаях отраженная волна отсутствует и частота отраженной волны (3) при c1 → υ1 уменьшается, в пределе вплоть до ω1 → 0. Из соотношения (3) следует, что изменение частоты отраженных волн включает постоянную во времени составляющую (которая определяется равномерной частью скорости движения границы, что соответствует эффекту Доплера), и переменную во времени составляющую. Изменение частоты наблюдается ограниченный промежуток времени, равный для постоянного ускорения
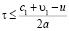 ,
,
и частота отраженных волн со временем уменьшается вплоть до ω1 → 0 в тот момент, когда увеличивающая за счет ускорения скорость движения «убегающей от падающей волны» границы раздела сред достигает скорости распространения падающей волны. За это время граница раздела сред смещается на расстояние равное
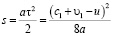 .
.
В наиболее простом, известном [1, 3] случае равномерно движущейся границы раздела также движущихся сред (a = 0, u ≠ 0) из уравнения (4) следуют соотношения
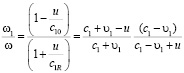 ,
, 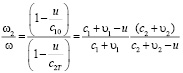 . (5)
. (5)
Если примыкающие к границе среды неподвижны, тогда υ1 = 0, υ2 = 0 и первое соотношение (5) дает известное соотношение для эффекта Доплера [2, 8]:
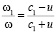 .
.
Второе соотношение (5) дает связь частот прошедшей и падающей волн:
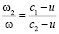 . (6)
. (6)
Это соотношение между частотами показывает возможность изменения частоты прошедшей волны только на границе сред с разными параметрами скорости распространения волн (c1 ≠ c2). На границе раздела сред с равными параметрами скорости частота прошедшей волны не меняется. В зависимости от направления движения границы и соотношения скоростей волны в средах частота отраженной и прошедшей волн может возрастать или уменьшаться. При u > 0 (волна и граница раздела движутся в одном направлении), частота отраженной волны ω1 < ω. Частота прошедшей волны ω2 > ω при условиях и 0 < u < c2 < c1 или при выполнении соотношения u < 0 < c1 < c2.
Практическое использование эффекта Доплера заключается в измерении скорости движения тел или границ путем сопоставления частот, падающей и отраженной волн. Тогда скорость ищется из соотношения (6) преобразованием
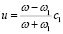
путем изменения частоты отраженной волны ω1, или из соотношения:
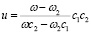
путем изменения частоты прошедшей волны ω2.
При движении сред (υ1, υ2≠0) эти соотношения существенно усложняются. Из соотношений (4) следует, что при наличии ускоренного движения границ измерение частотного сдвига или отраженной, или прошедшей через границу раздела двух сред волн позволяют измерить уже не скорость движения границ, а параметр u + (at / 2). Таким образом, все выводы [1], основанные на измерении скорости движения u, как измерения смещения частот становятся ошибочными. Причем погрешность изменения скорости за счет измерения сдвига частоты прошедшей волны меньше из-за меньшей зависимости ее частоты от параметра at (рис. 2).
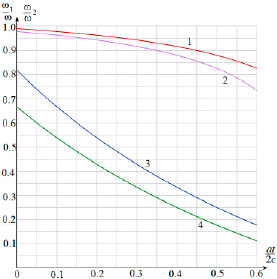
Рис. 2. Изменение частоты отраженной (1, 2) и прошедшей (3, 4) волн (u/c = 0,1–1,3; u/c = 0,2–2,4; - ω1 /ω – 3,4; ω2 /ω – 1,2)
Соотношение (4) может быть использовано для измерения ускорения, с которым движется граница раздела сред последовательным измерением сдвига частот через малый интервал времени τ:
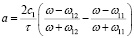 ,
,
где ω11, ω12 – частоты отраженной волны, измеренные c интервалом времени τ.
В случае неравномерного движения границы раздела сред (a ≠ 0) зависимость от нормированного времени относительного изменения частоты отраженной и прошедшей волн показана на рис. 2. Смещение частоты по эффекту Доплера зависит только от скорости и не зависит от времени. Смещение частоты, происходящее за счет ускоренного движения границы раздела, зависит от времени и становится определяющим через промежуток времени t~u/a даже при малой величине ускорения a, когда выполняется условие at~u.
Заключение
Стационарное изменение частоты волн, наблюдающееся при их при отражении от равномерно движущихся границ раздела сред, зависит не только от скорости движения границ, но и от параметров граничащих сред. При отражении от неравномерно движущихся тел (границы этих тел) возникает дополнительное нестационарное во времени изменение частоты, величина которого зависит от величины ускорения движения границы. Этот сдвиг частоты может существовать и в те моменты, когда эффект Доплера отсутствует (в те моменты, когда скорость движения границы равна нулю (u = 0)). Измерение частоты отраженных волн может быть использовано для измерения ускорения, с которым движутся границы раздела сред.


 science-review.ru
science-review.ru