science-review.ru
Введение
Посадочный модуль (ПМ) в виде летательного аппарата (ЛА) совершает посадку на Землю. В точке входа в атмосферу известны параметры движения ПМ. Определение текущих параметров движения осуществляется по информации, поступающей с бесплатформенного инерциального блока (БИБ), посредством бортового вычислительного цифрового комплекса (БЦВК), то есть при помощи бесплатформенной инерциальной навигационной системы (БИНС). Считается, что на момент входа в атмосферу ошибки БИНС в определении координат и скоростей полностью скомпенсированы, а ошибки углового положения скомпенсированы полностью или с конечной точностью.
На основе программно-математической модели движения было сформировано два варианта управления, приводящие ЛА в заданную точку на поверхности Земли. В варианте 1 реализован известный алгоритм «прямого наведения» [1, с. 129], а для варианта 2 был разработан алгоритм управления, позволяющий уложиться в ограничение на величину угла наклона траектории [2]. Для обоих вариантов управления была проведена оценка его точности в зависимости от шага формирования.
Вдоль полученных траекторий движения ЛА сымитированы показания БИБ, по которым осуществляется расчет текущей навигации и ориентации посредством реализованного алгоритма БИНС. На полученных вариантах траектории движения ЛА произведена оценка влияния на точность БИНС инструментальных ошибок акселерометров и ДУС и погрешностей задания начальной угловой ориентации, а также влияния формы траектории движения. На основе данных о точности управления и точности БИНС была произведена оценка точности системы управления в целом.
В работе приняты следующие глобальные допущения: не учитывается суточное вращение Земли; не учитывается влияние ветра; поверхность Земли представляет собой сферу.
Цель исследования – оценка точности системы управления посадочного модуля с бесплатформенным инерциальным блоком.
Материалы и методы исследования
БИНС представляет собой БИБ и алгоритм БИНС, реализуемый в БЦВК. БИБ, в свою очередь, содержит акселерометры и датчики угловой скорости (ДУС) в количестве, необходимом для получения полной информации о поступательном и угловом движениях объекта. С помощью ДУС возможно получение (пересчет) информации об угловой ориентации объекта относительно инерциальной системы координат (ИСК) и пересчет приращения кажущейся скорости (по информации, поступающей с акселерометров) из связанной системы координат (ССК) в ИСК [3, с. 54, 56]. В целом получаем навигационную информацию в виде координат и скорости объекта управления в ИСК. Информация, поступающая с акселерометров и ДУС, является входной для алгоритма БИНС. В данной работе считаем, что БИБ состоит из трех акселерометров и трех ДУС, оси чувствительности которых ортогональны и расположены по связанным осям ЛА.
Точность БИНС в определении координат и скоростей вычисляется по следующим формулам (параметры движения, получаемые путем интегрирования уравнений движения, считаются траекторными (идеальными) и обозначаются с нижним индексом «ТР», а параметры движения, получаемые с алгоритма БИНС, обозначаются с нижним индексом «Б»):
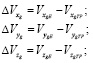
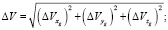(1)
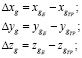
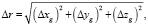
где ΔVxg – ошибка БИНС в определении х-составляющей скорости в земной системе координат (ЗСК); ΔVyg – ошибка БИНС в определении y-составляющей скорости в ЗСК; ΔVzg – ошибка БИНС в определении z-составляющей скорости в ЗСК; ΔV – ошибка БИНС в определении скорости в ЗСК; Δxg – ошибка БИНС в определении координаты х в ЗСК; Δyg – ошибка БИНС в определении координаты у в ЗСК; Δzg – ошибка БИНС в определении координаты z в ЗСК; Δr – ошибка БИНС в определении местоположения в ЗСК.
Таким образом, по формулам (1) производится оценка точности БИНС в определении скорости и геометрических координат.
Для расчета точности БИНС в определении углового положения на выходе алгоритма БИНС имеется матрица Т перехода от ССК к ЗСК, вычисляемая путем решения матричного уравнения Пуассона [4, с. 55], которую обозначим ТБ в соответствии с принятым выше. Траекторная матрица ТТР выражается следующим образом:
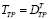(2)
где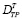 
– траекторная матрица D.
Введем произведение матриц
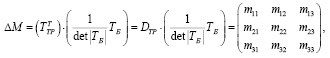(3)
результатом которого является матрица ΔМ. Матрицу ΔМ назовем матрицей углового расхождения, которая характеризует отличие матрицы ТБ от матрицы ТТР. В формуле (3) для матрицы ТБ применена операция нормировки путем деления каждого ее элемента на ее же определитель det|TБ|, так как при численных расчетах в алгоритмах БИНС матрица направляющих косинусов имеет свойство терять ортогональность, и невыполнение операции нормировки привело бы к дальнейшей некорректной оценке угловой погрешности БИНС.
Матрица углового расхождения может быть задана и при использовании матрицы, составленной с помощью параметров Родрига – Гамильтона [5]
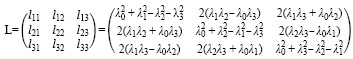, (4)
где λ0, λ1, λ2, λ3 – параметры Родрига – Гамильтона, задающие пространственный разворот между угловыми ориентациями, заданными матрицами направляющих косинусов ТБ и ТТР.
Имеем равенство матриц ΔМ (3) и L (4). Две матрицы равны, если равны их соответствующие элементы: mij = lij. Таким образом, существует возможность составить необходимое число уравнений для нахождения λ0, λ1, λ2, λ3.
Путем рассуждений была составлена следующая система для нахождения λ0,λ1,λ2,λ3:
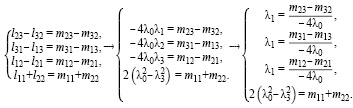(5)
Подставив выражение для λ3 (третье уравнение системы (5)) в четвертое уравнение системы (5) и решив полученное уравнение, получим выражение для λ0
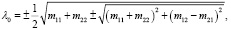(6)
где знаки для λ0 будут определены чуть позже.
Зная параметры λ0, λ1, λ2, λ3, можно вычислить параметры вектора конечного поворота Фх, Фу, Фz c нормой Ф, зная которые можно оценить погрешность БИНС в определении углового положения [6]. Параметры Фх, Фу, Фz вычисляются по следующим формулам:
o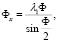 
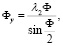(7)
o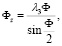 
o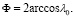 
Так как используемый при моделировании алгоритма БИНС шаг интегрирования Δt = 4 мс мал, то от шага к шагу будет мала и норма вектора конечного поворота Ф, а значение cos малой величины ≈1, то есть λ0 ≈ 1, λ0 > 0, также матрица ΔM будет близка к единичной, поэтому в формуле (7) выбираем знаки «+».
Найдя таким образом параметры Фх, Фу, Фz, по формуле (8) можно вычислить погрешность БИНС в определении углового положения:
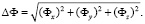(8)
Вычисление параметров навигации и ориентации, так же как и интегрирование уравнений движения, осуществляется методом Рунге–Кутты 4 порядка с шагом 4 мс. В качестве начальных значений координат вводятся координаты точки входа в атмосферу.
Результаты исследования и их обсуждение
Результаты моделирования работы БИНС представлены на графиках изменения погрешностей БИНС в определении скорости ΔV(t), определении координат Δr(t), определении угловой ориентации ΔФ(t) для вариантов 1 (рис. 1–3, а) и 2 (рис. 1–3, б) траектории движения.
Данные погрешности являются методическими погрешностями алгоритма БИНС [7; 8].
Значения представленных погрешностей БИНС (вариант 1) на конечный момент времени следующие: ΔV(t) = 0,12 м/с, Δr(t) = 7,5 м, ΔФ(t) = 0,05′. Значения методических погрешностей БИНС (вариант 2) на конечный момент времени для данного варианта траектории движения следующие: ΔV(t) = 0,05 м/с, Δr(t) = 1,3 м, ΔФ(t) = 0,02′.
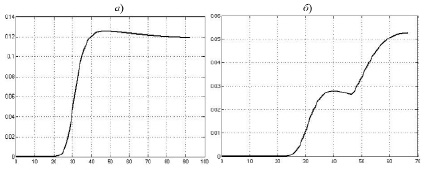
Рис. 1. Графики изменения ошибки ΔV(t)
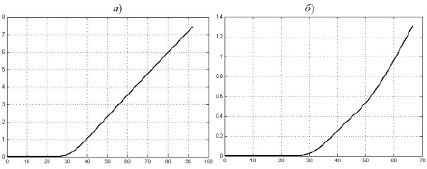
Рис. 2. Графики изменения ошибки Δr(t)
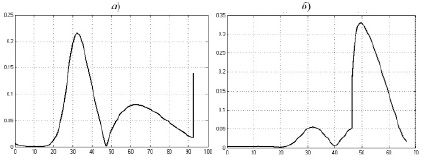
Рис. 3. Графики изменения ошибки ΔФ(t)
Величины методических погрешностей небольшие и, как видно из рис. 1–3, мало зависят от начальных условий, поэтому в дальнейшем была проведена их компенсация, чтобы оценить влияние только инструментальных ошибок БИБ и ошибок задания начальной ориентации на точность БИНС.
Проведена оценка влияния ошибок БИБ и погрешности задания начальной ориентации на точность навигации на траектории движения варианта 1, дополнив существующую модель в Simulink Matlab возможностью задавать погрешности смещения нуля и погрешности масштабного коэффициента по каждому акселерометру и ДУС, а также возможностью вносить погрешности задания начальной ориентации.
Анализируя полученные данные, можно сделать следующие выводы:
– при наличии погрешности смещения нуля ΔAi [8] у i-го акселерометра, максимальные погрешности БИНС возникают по соответствующим i-м составляющим (например, при наличии погрешности ΔAx – максимальные погрешности в определении координаты xg и составляющей скорости Vxg); то же справедливо и при наличии δKai;
– наибольшее влияние из инструментальных погрешностей ДУС оказывают инструментальные погрешности ДУС Гу и Гz, при этом самое сильное влияние оказывает δKωz;
– наибольшее влияние на погрешности БИНС оказывают погрешности задания начальной ориентации Δψk, Δϑk, Δγk (углы рыскания, тангажа и крена) [9] при этом самое сильное влияние оказывает погрешность задания Δϑk;
– j-я составляющая погрешностей БИНС от действия k-го фактора со знаком «+» равна j-й составляющей от действия фактора со знаком «–», но с противоположным знаком (например, Δxg (ΔAx) = -Δxg (-ΔAx) ); это справедливо для всех составляющих погрешностей БИНС за исключением ΔV, Δr и ΔФ;
– погрешности БИНС (3σ) на конечный момент времени при действии всех факторов в определении координат Δr не превышают 234 м, в определении скорости ΔV не превышают 4,1 м/с, в определении угловой ориентации ΔФ не превышают 6,1′.
По изменениям погрешностей БИНС во времени можно отметить следующее:
– резкий рост погрешностей в определении координат и составляющих скорости происходит с момента времени t ≈ 30 c, что соответствует максимальным перегрузкам по связанным осям;
– погрешность определения ориентации в начальный момент времени равна
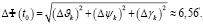
Для оценки погрешностей БИНС на траектории движения варианта 2 был применим тот же подход, что и при оценке погрешностей БИНС на варианте 1 траектории движения с единственным отличием в том, что будем задавать факторы, влияющие на точность БИНС, только со знаком «+», так как было выявлено, что j-я составляющая погрешностей БИНС от действия k-го фактора со знаком «+» равна j-й составляющей от действия фактора со знаком «–», но с противоположным знаком.
Анализируя полученные данные, можно сделать такие же выводы, как и по результатам варианта 1 траектории движения. Однако погрешности БИНС на конечный момент времени при действии всех факторов в определении координат Δr не превышают 128 м, в определении скорости ΔV не превышают 3,9 м/с, в определении угловой ориентации ΔФ не превышают 4,9′.
По изменениям погрешностей БИНС во времени аналогично варианту 1 траектории движения можно отметить следующее:
– резкий рост погрешностей в определении координат и составляющих скорости происходит с момента времени t ≈ 30 c, что соответствует максимальной продольной перегрузке;
– погрешность определения ориентации в начальный момент времени равна
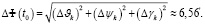
Сравнивая между собой погрешности БИНС, полученные на двух вариантах траектории движения при действии всех факторов, можно отметить, что на варианте 2 погрешность БИНС определения местоположения Δr на конечный момент времени почти в 2 раза меньше, чем на варианте 1, что может быть связано с меньшим временем движения. Ошибки определения скорости ΔV и угловой ориентации ΔФ в обоих случаях приблизительно равны. С точки зрения использования БИНС предпочтительнее использование варианта 2 управления, дающего вариант 2 траектории движения, так как в этом случае время движения до точки цели меньше и меньше погрешность определения местоположения, чем на траектории движения варианта 1.
Результаты показывают, что точность СУ в основном определяется точностью БИНС. Однако управление было сформировано с учетом точных знаний атмосферы, аэродинамических коэффициентов и без учета запаздывания формирования навигации, поэтому влияние этих факторов на точность формирования управления требует дополнительного исследования.
Заключение
В данной работе была проведена оценка точности системы управления посадочного модуля с бесплатформенным инерциальным блоком двух вариантов управления, приводящих ЛА в заданную точку на поверхности Земли. Показано, что предпочтительнее использование варианта 2 управления, так как в этом случае время движения до точки цели меньше и меньше погрешность определения местоположения ЛА.
Результаты данной работы могут быть использованы при разработке требований к БИБ и БЦВК, а также при формировании тестовых траекторий посадочного модуля на атмосферном участке при заданных начальных и конечных параметрах движения
Для дальнейших исследований возможно уточнение математической модели посредством учета влияния суточного вращения и реальной формы поверхности Земли, учета влияния ветра, учета динамики вращения вокруг центра масс. При формировании управления возможен учет ограничений на величины максимально допустимой перегрузки и аэродинамического нагрева, а также учет запаздывания формирования навигационной навигации. При оценке точности БИНС возможно расширение моделей погрешностей акселерометров и ДУС и использование многошаговых алгоритмов БИНС.