Введение
Интерактивная карта – современный и крайне удобный способ представления геоданных с множеством функций, среди которых одна из самых востребованных – это навигация [1]. Но для реализации поиска оптимальных маршрутов на интерактивной карте офиса, помещения или другого замкнутого пространства необходимо иметь соответствующий навигационный граф, по которому будут строиться кратчайшие пути. Поэтому можно считать актуальным разработку алгоритма для генерации навигационного графа на основе схемы помещения.
Цель исследования – рассмотреть основные шаги разработанного алгоритма генерации навигационного графа для помещений на основе скелета его схемы, формирующегося с использованием метода Straight Skeleton.
Материалы и методы исследования
Задачу, которую решает исследуемый алгоритм, можно сформулировать следующим образом: необходимо построить оптимальный навигационный граф на основании схемы помещения для последующего его использования в определении оптимальных маршрутов на интерактивной карте.
Навигационный граф – структура, моделирующая набор возможных маршрутов внутри помещения или любого другого пространства, для которого есть необходимость анализа и поиска кратчайших путей или любых других задач, связанных с графами. Каждая вершина имеет координаты по OX и OY. Ребра соединяют вершины между собой и могут иметь предустановленный вес [2].
Критерием оптимальности графа можно считать адекватное как количество, так и расположение вершин графа в двумерном пространстве, а также набор ребер, соединяющих узлы графа.
Построенная структура помещения должна позволять строить оптимальный маршрут от одной точки до другой так, чтобы быть максимально схожим с тем, как человек добирается от одного места к другому в реальной жизни.
Поэтому граф обязательно должен быть связным, либо в случае наличия набора островных точек необходимо потом вручную их удалять или соединять с графом другого помещения (этажа).
Минимизация количества вершин и ребер графа связана с необходимостью хранить его отдельно в базе данных и памяти приложения. Поэтому важно получить такой набор вершин и ребер, который позволит эффективно строить кратчайшие пути и при этом не будет занимать много памяти.
Общая структура разработанного алгоритма представлена на следующей схеме (рис. 1). Далее последует подробный разбор каждого шага алгоритма из представленной схемы и применяемых методов.
Методы Medial Axis и Straight Skeleton
В основе алгоритма лежат методы для построения скелета помещения, из которого далее будут выделяться ключевые точки и проводиться ребра графа. Среди наиболее популярных методов можно выделить два основных: Medial Axis (медиальная ось) и Straight Skeleton (прямолинейный скелет).
Medial Axis можно рассматривать как отдельное определение – набор точек, имеющих более одной ближайшей точки на контуре геометрического объекта. То есть для каждой точки медиальной оси можно построить окружность определенного радиуса, и она будет касаться внешнего контура в двух и более точках [4].
Таким образом, получается топологический скелет, который определяет форму и сохраняет основные детали геометрической фигуры.
Straight Skeleton же сильно схож с Medial Axis, но имеет отличие в использовании преимущественно прямых отрезков в своей основе, в то время как медиальная ось может включать в себя параболические кривые (рис. 2) [5].
Именно данное различие повлияло на выбор прямолинейного скелета в качестве основы для рассматриваемого алгоритма, так как такой формат позволит проще определять ключевые точки. Рассматриваемый алгоритм можно адаптировать и под использование Medial Axis в качестве скелета помещения, но придется переопределить набор ключевых точек.
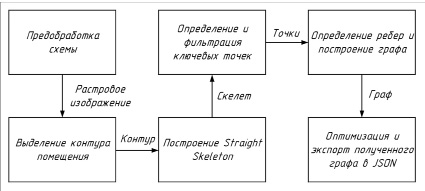
Рис. 1. Схема алгоритма Источник: составлено авторами на основе [3]
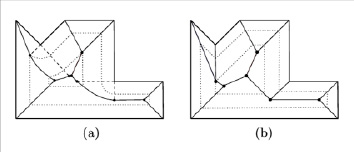
Рис. 2. Сравнение скелетов многоугольника (а – Medial Axis, b – Straight Skeleton) Источник: составлено авторами на основе источников [4; 5]
Предобработка схемы
Перед выполнением основных шагов алгоритма необходимо провести преобразование схемы помещения. Нужно убрать лишние детали, которые могут помешать определить контур и скелет помещения, и преобразовать схему (из SVG или другого формата) в растровое изображение.
Так как в итоге выполнения алгоритм экспортирует граф с координатами по OX и OY, то важно, чтобы загружаемое изображение было оригинального разрешения для корректного наложения полученного графа при загрузке в интерактивную карту.
В случае с форматом SVG это делается достаточно просто, если правильно настроена разметка, которая позволит вручную или программно удалить лишние части схемы. Но при преобразовании такой схемы в растровое изображение могут возникнуть проблемы с масштабированием, особенно при использовании онлайн-сервисов. Здесь необходимо определить коэффициент масштабирования разрешения схемы, временно уменьшить ее разрешение с помощью SVG-атрибутов кратно полученному коэффициенту и выполнить преобразование в растр.
В итоге изображение обрабатывается алгоритмом: выполняется загрузка, бинаризация и устранение шумов, которое убирает небольшие помехи и не препятствует дальнейшему формированию корректного контура помещения.
Выделение контура помещения
Далее следует шаг по вычислению контура помещения. Данный алгоритм реализован в математических пакетах языка программирования Python, поэтому для построения контура использовалась функция библиотеки OpenCV findContours.
Важно также при определении контура использовать в функции для параметра mode значение RETR_TREE для получения иерархии контуров и далее объединить эту иерархию в единый полный контур помещения. Это необходимо для последующей оптимизации ребер графа. На выходе получается бинарная матрица, которая показывает, есть ли точка контура для конкретного пикселя изображения.
Построение скелета помещения
Далее необходимо построить скелет помещения. Метод Straight Skeleton реализован в библиотеке skimage.morphology и представлен функцией skeletonize. Также в библиотеке есть функция medial_axis для построения медиальной оси изображения, так что алгоритм можно доработать и выборочно использовать как прямолинейный скелет, так и медиальную ось в качестве основы для генерации графа. Но в случае Medial Axis будут отличаться дальнейшие шаги по выделению ключевых точек из-за ранее упомянутых различий двух подходов к построению скелета. На выходе данного блока алгоритма также получается бинарная матрица, которая показывает, присутствует ли точка скелета в конкретном пикселе изображения.
Выделение и фильтрация ключевых точек
Далее предстоит выделить ключевые точки скелета, которые станут вершинами графа. Для всех точек прямолинейного скелета (в виде бинарной матрицы) можно применить 8-связный шаблон: пиксель считается связанным с другим, если является соседом как по горизонтали, так и по диагонали матрицы [3].
Выделяемые ключевые точки можно поделить на 3 типа:
1. Листья – в качестве соседа имеют только одну точку. Обычно представляют собой переходы в кабинеты, лестницы, лифты и т.д.
2. Узлы – в качестве соседей имеют 3 и более точек, то есть являются разветвляющими точками.
3. Точки изгиба – с них начинается изгиб отрезков прямолинейного скелета, то есть для этих точек применим формат шаблона, при котором они имеют одного горизонтального соседа и при этом одного соседа по диагонали, что отражает положение точки на углу (не 90° и 180°) соединения двух отрезков скелета.
Так как количество точек после их поиска на скелете может получиться огромным (особенно точек изгиба из-за неровности отрезков), то необходимо отфильтровать их относительно друг друга по расстоянию между собой. Было определено, что оптимально фильтровать каждый полученный набор точек по отдельности, листья относительно узлов и точки изгиба относительно набора узлов и листьев.
Так как приемлемое расстояние между точками может зависеть от разрешения изображения, то предусмотрено назначение минимальных допустимых расстояний в качестве констант. На выходе получается три набора ключевых точек, для которых определены их координаты по OX и OY.
Построение графа
Следующим шагом алгоритма будет непосредственно формирование графа на основе ранее выделенных ключевых точек. Но сначала необходимо понять, как проводить ребра между вершинами.
Принцип формирования ребер между ключевыми точками следующий: для каждой вершины проводятся аппроксимированные отрезки к другим ключевым точкам, и если данное ребро пересекает или проходит слишком близко к полному контуру помещения, то это ребро не рассматривается. Все остальные ребра сохраняются и входят в сформированный граф [3]. Такой подход позволит соединять между собой только те точки, на пути которых нет преград.
Оптимизация полученного графа
Но полученный набор ребер все равно избыточен из-за множества перекрестных соединений или соединений под слишком острыми или тупыми углами. Самым оптимальным набором ребер можно считать такой набор, в котором соединения идут под ~45°, ~90° и ~180° [6].
Поэтому необходимо отфильтровать полученный набор ребер с учетом неоптимальных углов. Сделать это можно перебором всех ребер, вычислением углов между ними с помощью формулы косинуса угла между векторами и удалением тех соединений, которые проходят под некорректным углом. Для этого также была выделена константа, определяющая «чувствительность» таких углов.
Дальше остается только экспортировать сформированный граф в нужный формат (например, JSON) и использовать его для построения кратчайших путей на интерактивной карте [1].
Результаты исследования и их обсуждение
В качестве примера работы алгоритма выбран третий этаж учебного корпуса № 3 кампуса Калужского филиала МГТУ им. Н.Э. Баумана. Схема этажа представлена в виде SVG-документа. Выполнено преобразование плана коридора в растровое изображение с сохранением оригинального разрешения. В результате выполнения алгоритма получается следующий граф, наложенный на схему коридора (рис. 3).
Результат программного поиска кратчайшего маршрута между аудиториями на интерактивной карте представлен на следующем изображении (рис. 4).
Хотя сейчас алгоритм генерирует вполне адекватный и рабочий граф, все равно есть моменты, которые можно усовершенствовать.
1. Объединение близких точек в кластеры. Вместо фильтрации можно объединять рядом стоящие вершины и аккумулировать все соединения в этот кластер. Данное улучшение сделает граф более подходящим для поиска реальных маршрутов [7].

Рис. 3. Результат применения алгоритма на схеме коридора третьего этажа УАК3 кампуса КФ МГТУ Источник: составлено авторами по результатам работы алгоритма
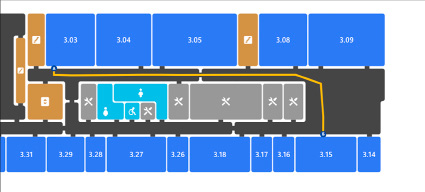
Рис. 4. Пример программного построения оптимального маршрута на основе сформированного графа Источник: составлено авторами по результатам работы алгоритма
2. Расширение области генерации графа до аудиторий. Сейчас граф строится только на однородном коридоре и не учитывает кабинеты. Это не очень удобно, так как приходится предобрабатывать схему, убирая лишние помещения и детали, и исключаются случаи, когда нужно расширить область графа до внутренних комнат.
3. Доработка фильтрации ребер. Сейчас алгоритм удаляет множество лишних ребер за счет выборки по углу, но часто отсекаются корректные ребра или остаются некорректные при небольших изменениях порогового угла.
4. Реализация собственного алгоритма скелетизации помещения. Это позволит на этапе построения прямолинейного скелета отсечь ненужные точки и оставить только ключевые, что повысит производительность алгоритма [5].
Заключение
В данной статье были рассмотрены основные шаги алгоритма построения графа для навигации внутри помещения и обоснован выбор метода Straight Skeleton вместо Medial Axis. Разработанный алгоритм позволяет быстро вычислять навигационный граф по схеме помещения, но имеет ряд недоработок, которые можно исправить в будущем.


 science-review.ru
science-review.ru