Повышение прочности и одновременно облегчение элементов различных конструкций достигается использованием волнистых тонких пластин, заменяющих ортотропные материалы, при проектировании строительных сооружений [1], [2], [3], [4], [5].

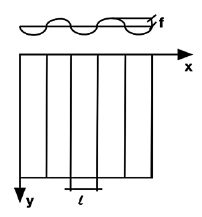
Рис.1.

Рассматривается прямоугольная гофрированная пластина, нагруженная распределённой нагрузкой, перпендикулярной срединной плоскости (Рис. 1). Форма волны пластины имеет вид: .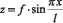

Пластинка рассматривается как конструктивно ортотропная плоская пластина с различными жёсткостями на изгиб. Дифференциальное уравнение изгиба ортотропной пластинки на упругом основании имеет вид [6] :

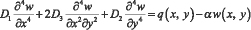(1)

где , ,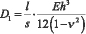

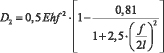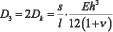, E и ? – упругие постоянные материала пластины, h – толщина пластины, 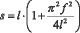– длина дуги полуволны.

Перейдя к безразмерным переменным ξ,η следующей заменой 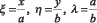получим (1) в следующем виде:

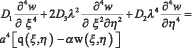(2)

Выражение прогиба w(ξ,η) выберем в виде двойного ряда: ,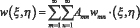

где w(ξ,η) – функция, удовлетворяющая статическим и кинематическим граничным условиям пластинки, Amn – неизвестные коэффициенты.

Функциональное уравнение метода Бубнова – Галёркина [7], [8] гофрированной пластинки на упругом основании, когда к пластине приложена распределённая нагрузка по всей поверхности и соприкасается с упругим основанием по всей поверхности пластины, примет вид:

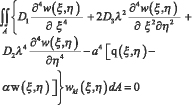(3)

k, l = 1,2,3,... После подстановки w(ξ,η) в (3) получим:

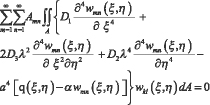(4)

k, l = 1,2,3,...

Рассмотрим различные случаи приложения нагрузки и опирания пластины на упругое основание. Систему линейных алгебраических уравнений (4) относительно неизвестных Amn можно представить в виде:

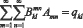, k, l = 1,2,3,... (5)

где

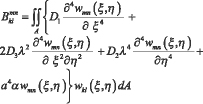(6)

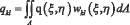(7)

Формулы (6) и (7) для 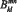и qkl получены для случая, если распределённая нагрузка действует на пластину по всей поверхности пластины и пластина соприкасается с упругим основанием по всей поверхности.

В случае, если пластина c упругим основанием соприкасается в точках волны, то (6) принимает вид:

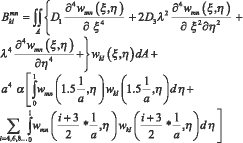
В случае, если распределённая нагрузка передаётся через рёбра пластины, то (7) принимает вид:

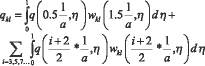
где l – длина волны, i – номер волны гофры пластины.

Определив коэффициенты Amn из системы линейных алгебраических уравнений (5), получим выражения w(ξ,η), которые позволяют определить неизвестные НДС пластины.