1
Кадомцева Е.Э. 1 Бескопыльный А.Н. 1 Бескопыльная Н.И. 1 Бердник Я.А. 1
1 Академия строительства и архитектуры Донского государственного технического университета
В статье рассматривается изгиб тонкой гофрированной пластины на упругом основании. В плане пластина прямоугольная. Гофр представляет собой волну по синусоиде, направленной параллельно одной из сторон пластинки. За расчётную схему принимается ортотропная плоская пластинка с разными цилиндрическими жёсткостями в двух взаимно перпендикулярных направлениях. За основную неизвестную НДС принимается прогиб пластины. Прогиб представляется как двойной ряд по функциям, удовлетворяющим граничным условиям с неизвестными коэффициентами. Задача решается методом Бубнова- Галёркина. Определение прогиба сводится к решению системы линейных неоднородных алгебраических уравнений относительно неизвестных коэффициентов. Получены выражения для коэффициентов и свободных членов системы линейных алгебраически уравнений, которые определяются через функции разложения, размеры пластины и приложенные нагрузки. Рассмотрены различные случаи соприкосновения пластины с упругим основанием, а также различные случаи приложения распределённой нагрузки.
гофрированная пластина
упругое основание
ортотропная
плоская пластина
прогиб
метод Бубнова- Галёркина
1. Кадомцева Е.Э., Бескопыльный А.Н.. Расчёт на прочность армированных балок с заполнителем из бимодульного материала с использованием различных теорий прочности. [Электронный ресурс] // «Инженерный вестник Дона», 2013, № 4. – режим доступа: www.ivdon.ru/ru/magazine/archive/n4y2013/2125 (доступ свободный)-Загл. с экрана . - Яз.рус.
2. Моргун Л.В., Богатина А.Ю., Кадомцева Е.Э. О поведении фибропенобетона при изгибе армированных балок. Бетон и железобетон - взгляд в будущее: научные труды I Всероссийской (П Международной) конференции по бетону и ж/б (Москва, 12-16 мая 2014) в 7 т. Т.3. Арматура и системы армирования. Фибробетоны и армоцементы. Проблемы долговечности. Москва : МГСУ, 2014. – С.151…157.
3. Кадомцева Е.Э. Прочность при ударе по составной балке. ”Строительство 2009”, Материалы юбилейной международной научно- практической конференции/Ростовский государственный строительный университет - Ростов-на-Дону: редакционно-издательский центр РГСУ, 2009
4. В.Н. Моргун, П.Н. Курочка, А.Ю. Богатина, Е.Э. Кадомцева, Л.В. Моргун. К вопросу о сцеплении стержневой арматуры с бетоном и фибробетоном. Ж. «Строительные материалы», 2014, №8. – С.56…59.
5. Е.Э. Кадомцева, Л.В. Моргун. Учёт влияния отличия модулей упругости на сжатие и растяжение при расчёте на прочность армированных балок с заполнителем из фибропенобетона. [Электронный ресурс] // «Инженерный вестник Дона», 2013, № 2. – режим доступа: www.ivdon.ru/magazine/archive/n2y2013/1655 (доступ свободный) - Загл. с экрана . - Яз.рус.
6. Прочность, устойчивость, колебания. Справочник в трёх томах. Под общей редакцией И.А. Биргер и Я.Г. Пановко. Т.2.,с.147 - М. изд-во” Машиностроение”, 1988.-832 с.464.
7. Мышкис А.Д. Прикладная математика для инженеров. Специальные курсы. –М. изд-во “Физматлит”, МАИК «Наука/Интерпериодика», 2007.-687 с.
8. Yin J.H. Comparative modeling study on reinforced beam on elastic foundation // ASCE Journ. of Geotechn. and Geoenvironmental Engineering. -2000. Vol. 126, № 3. -P. 265-271.
Повышение прочности и одновременно облегчение элементов различных конструкций достигается использованием волнистых тонких пластин, заменяющих ортотропные материалы, при проектировании строительных сооружений [1], [2], [3], [4], [5].
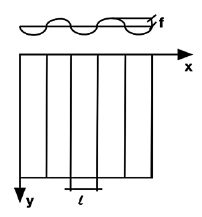
Рис.1.
Рассматривается прямоугольная гофрированная пластина, нагруженная распределённой нагрузкой, перпендикулярной срединной плоскости (Рис. 1). Форма волны пластины имеет вид: 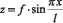 .
.
Пластинка рассматривается как конструктивно ортотропная плоская пластина с различными жёсткостями на изгиб. Дифференциальное уравнение изгиба ортотропной пластинки на упругом основании имеет вид [6] :
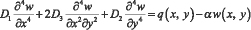 (1)
(1)
где 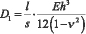 ,
, 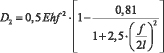 ,
,
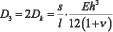 , E и ? – упругие постоянные материала пластины, h – толщина пластины,
, E и ? – упругие постоянные материала пластины, h – толщина пластины, 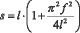 – длина дуги полуволны.
– длина дуги полуволны.
Перейдя к безразмерным переменным ξ,η следующей заменой 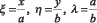 получим (1) в следующем виде:
получим (1) в следующем виде:
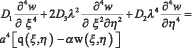 (2)
(2)
Выражение прогиба w(ξ,η) выберем в виде двойного ряда: 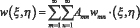 ,
,
где w(ξ,η) – функция, удовлетворяющая статическим и кинематическим граничным условиям пластинки, Amn – неизвестные коэффициенты.
Функциональное уравнение метода Бубнова – Галёркина [7], [8] гофрированной пластинки на упругом основании, когда к пластине приложена распределённая нагрузка по всей поверхности и соприкасается с упругим основанием по всей поверхности пластины, примет вид:
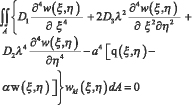 (3)
(3)
k, l = 1,2,3,... После подстановки w(ξ,η) в (3) получим:
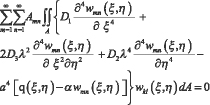 (4)
(4)
k, l = 1,2,3,...
Рассмотрим различные случаи приложения нагрузки и опирания пластины на упругое основание. Систему линейных алгебраических уравнений (4) относительно неизвестных Amn можно представить в виде:
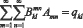 , k, l = 1,2,3,... (5)
, k, l = 1,2,3,... (5)
где
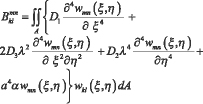 (6)
(6)
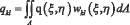 (7)
(7)
Формулы (6) и (7) для 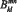 и qkl получены для случая, если распределённая нагрузка действует на пластину по всей поверхности пластины и пластина соприкасается с упругим основанием по всей поверхности.
и qkl получены для случая, если распределённая нагрузка действует на пластину по всей поверхности пластины и пластина соприкасается с упругим основанием по всей поверхности.
В случае, если пластина c упругим основанием соприкасается в точках волны, то (6) принимает вид:
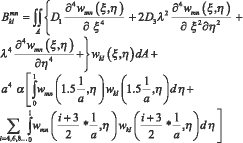
В случае, если распределённая нагрузка передаётся через рёбра пластины, то (7) принимает вид:
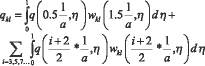
где l – длина волны, i – номер волны гофры пластины.
Определив коэффициенты Amn из системы линейных алгебраических уравнений (5), получим выражения w(ξ,η), которые позволяют определить неизвестные НДС пластины.
Библиографическая ссылка
Кадомцева Е.Э., Бескопыльный А.Н., Бескопыльная Н.И., Бердник Я.А. РАСЧЁТ НА ЖЁСТКОСТЬ ГОФРИРОВАННОЙ ПЛАСТИНЫ НА УПРУГОМ ОСНОВАНИИ МЕТОДОМ БУБНОВА-ГАЛЁРКИНА // Научное обозрение. Технические науки. 2016. № 6.
С. 33-35;
URL: https://science-engineering.ru/ru/article/view?id=1124 (дата обращения: 04.02.2026).

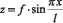 .
.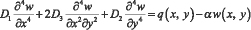 (1)
(1)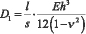 ,
, 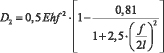 ,
,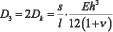 , E и ? – упругие постоянные материала пластины, h – толщина пластины,
, E и ? – упругие постоянные материала пластины, h – толщина пластины, 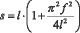 – длина дуги полуволны.
– длина дуги полуволны.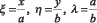 получим (1) в следующем виде:
получим (1) в следующем виде: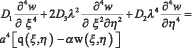 (2)
(2)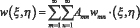 ,
,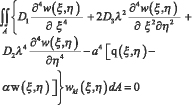 (3)
(3)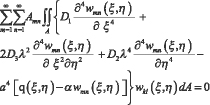 (4)
(4)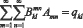 , k, l = 1,2,3,... (5)
, k, l = 1,2,3,... (5)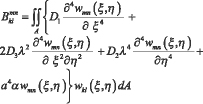 (6)
(6)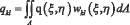 (7)
(7)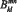 и qkl получены для случая, если распределённая нагрузка действует на пластину по всей поверхности пластины и пластина соприкасается с упругим основанием по всей поверхности.
и qkl получены для случая, если распределённая нагрузка действует на пластину по всей поверхности пластины и пластина соприкасается с упругим основанием по всей поверхности.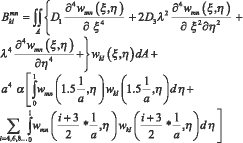


 science-review.ru
science-review.ru