science-review.ru
Изучение механизмов внутреннего трения в твердых телах имеет, по меньшей мере, два аспекта практического использования. Во-первых, метод внутреннего трения является очень информативным и тонким методом исследования структуры и свойств конденсированного состояния. Например, этим методом можно определять коэффициенты диффузии примеси в кристаллах в условиях низких и комнатных температур, когда получение этих величин из диффузионного опыта затруднительно и требует высокой точности измерения малых концентраций, а также значительной продолжительности проведения эксперимента. Метод внутреннего трения позволяет определять основные параметры дефектной структуры кристаллов, распределения структурных дефектов по геометрическим признакам, параметры равновесного и неравновесного фазового состояния и т.д. В некоторых случаях этот метод является единственным для измерения отдельных параметров. Во-вторых, понимание механизмов процесса позволяет прогнозировать физические свойства новых материалов и проектировать их состав и структуру с целью получения высоких демпфирующих свойств.
Известно, что границы зерен являются важнейшим типом дефектов в поликристаллических материалах. Их состояние и физические процессы с их участием в значительной степени определяют поведение материала в условиях внешних воздействий полей различной природы. При аналитическом рассмотрении проскальзывания по границам и обусловленного им внутреннего трения сами границы обычно принимаются плоскими. Реальные границы неизбежно содержат различные отклонения от плоской конфигурации. В общем случае при разориентации зерен, близкой к специальной, границы имеют фасетированную структуру. Описание кинетики фазового перехода фасетирования межзеренных границ дано в работах [1 – 3]. Подобная структура поверхностей раздела в металлах приводит к ряду особенностей протекания релаксационных процессов с их участием [4]. Возросший интерес к изучению механизмов релаксационных процессов в твердом теле актуален не только в связи с развитием физики конденсированного состояния, но также и рядом приложений этой науки к техническим проблемам [5].
Целью настоящей работы является описание механизмов зернограничного внутреннего трения при нагружении материала периодической внешней силой.
Модели высокотемпературного фона
Примем модель, в которой граница имеет структуру из симметрично чередующихся плоских фасеток, расположенных под углами ±α к некой воображаемой усреднённой плоскости, вдоль которой действует переменное сдвиговое напряжение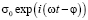 
, где σ00 – амплитуда. Поверхность границы гофрирована, с размером фасеток в одном направлении порядка размера зерна. Такая структура является одномерно фасетированной. Под действием напряжения сегменты поочерёдно становятся источниками и стоками вакансий в зависимости от времени. Можно считать, что в пределах каждого сегмента действует периодический источник 
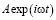, фаза которого в общем случае не совпадает с напряжением.
Исходя из симметрии задачи, достаточно рассмотреть один такой сегмент-фасетку ширины L, наклонённый под углом α к направлению внешнего сдвигового напряжения. Координатные оси выберем в плоскости фрагмента так, что ось x направлена вдоль отрезка направляющей ломаной линии, а y – вдоль образующей. Задача диффузии вакансий является одномерной, поскольку мы пренебрегаем потоком их в объём зёрен по сравнению с граничными потоками по причине малости отношения коэффициентов объемной и граничной диффузии.
Для избыточной концентрации вакансий на сегменте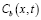 
можно записать неоднородное уравнение диффузии:
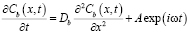.(1)
Здесь Db – коэффициент зернограничной диффузии вакансий. Симметрия диктует выполнение граничных условий
.
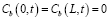Решаем задачу методом Фурье. С этой целью представляем постоянную A в (1) в виде ряда по синусам. Решение (1) имеет вид
,
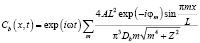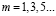(2)
Здесь введены обозначения:
,
,
,
.
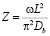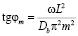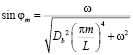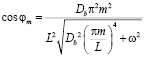При невысоких значениях внешнего напряжения нормальное напряжение σn на сегменте линейно связано с избыточной концентрацией вакансий на нём:
,
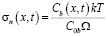где Ω – атомный объём. С учетом (2) это дает [6]:
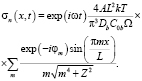(3)
Скорость движения зёрен определяется плотностью потока j вакансий из сегмента через обе его границы:
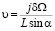, (4)
где δ – диффузионная толщина границы. Находя поток и подставляя его в (4), получим
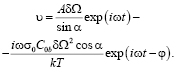(5)
Внутреннее трение, обусловленное вкладом одного сегмента длиной y, равно
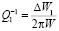. (6)
Здесь в числителе стоит энергия, рассеянная за цикл
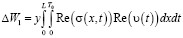
на площади сегмента. В знаменателе величина
,
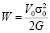где G – модуль сдвига, равна упругой энергии зерна. Величину А найдем, учитывая т.н. эффект подстройки напряжений [7]. С этой целью приравняем величину сил внешнего и внутреннего напряжений на сегменте
.
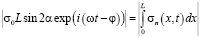За объём зерна примем
,
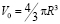где R – средний его размер. Учитывая предыдущие формулы, найдем величину внутреннего трения [8]:
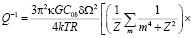
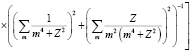.(7)
Геометрический множитель κ учитывает долю принадлежности границы зерну и его реальную форму.
Размеры фасеток на границах зерен могут значительно различаться. Интересен случай бимодального их распределения. Если один вид фасеток имеет малый размер относительно другого, и угол взаимного наклона их близок к прямому, то такие границы называют ступенчатыми. Проскальзывание по ним имеет диффузионный характер [9]. Рассмотрим границу, состоящую из равноотстоящих друг от друга ступенек высоты d чередующихся знаков. Между ними расположены протяженные плоские участки длины 2l. Переменное сдвиговое напряжение, действующее на них, приводит к тому, что на ступеньках противоположного знака возникают растягивающие и сжимающие напряжения. Это влечет изменение химического потенциала вакансий и их диффузии между ступеньками. Решение диффузионной задачи, подобной описанной выше с периодическими источниками на ступеньках, приводит к выражению для скорости и напряжения:
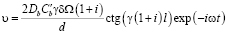, (8)
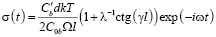. (9)
Здесь
,
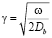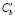– константа, определяющая амплитуду концентрации на ступеньке,
,
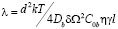η – эффективная вязкость границы.
Повторяя выкладки, подобные приведенным ранее, после преобразований получаем [10] выражение для величины внутреннего трения:
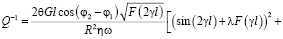
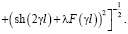(10)
, 
, 
.
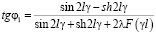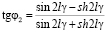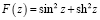Избыточные вакансии в объеме зерна имеют тенденцию оседать на границах, где они при определенных условиях могут образовать поры. В [11] предложена двумерная модель внутреннего трения на границах, имеющих параллельные ступеньки и цилиндрические поры диаметра, равного размеру ступенек. Симметрия граничных условий теряется, поэтому граница в условиях действия переменного сдвигового напряжения является источником и стоком вакансий для объемной диффузии. В двух предельных случаях внутреннее трение имеет вид:
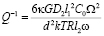, (11)
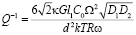. (12)
Выражение (11) описывает область низких частот или высоких температур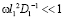 
, а (12) – обратную ситуацию. D1 и D2 – зернограничный и объемный коэффициенты диффузии, l1 – расстояние между ступенькой и порой, l2 – расстояние от границы до стоков вакансий в объеме.
На основе приведенной модели можно описать высокотемпературный фон внутреннего трения в двумерно фасетированных границах. Необходимо учесть диффузионные потоки в двух независимых направлениях в границе. Если пренебречь объемными диффузионными потоками, то можно ограничиться рассмотрением картины диффузии по развертке граничной поверхности, которая имеет различный вид в соответствующих частных случаях. Решение диффузионной задачи в общем случае приводит [4, 12] к выражению:
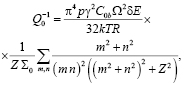(13)
где m и n принимают значения 1, 3, 5,..., а коэффициент p учитывает геометрию границы.
Пики внутреннего трения
В то время как проскальзывание по границе в целом имеет диффузионный характер вследствие наличия на фасетках нормальных составляющих напряжений, проскальзывание по самим фасеткам под действием касательных напряжений имеет консервативный характер. Такое проскальзывание ограничивается линиями сопряжения фасеток, а в центральной их области имеет наибольший размах. В приближении квазиоднородного сдвига, ограниченного линейными дефектами дислокационного типа в линиях, ограничивающих фасетки, можно найти величину внутреннего трения. Его частотная зависимость имеет характер дебаевского пика. Подробное рассмотрение вопроса [12 – 14] приводит к выражению для частотной зависимости величины затухания колебаний
,
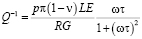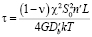, (14)
Здесь R – размер зерна, ν – коэффициент Пуассона, G – модуль сдвига, L – ширина фасетк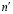и, 
и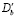 
– концентрация и коэффициент диффузии примеси в границе.
Полученное выражение хорошо согласуется с экспериментально полученным спектром в ультрамелкозернистой меди, приготовленной методом равноканального углового прессования с последующей прокаткой [15].
Границы зерен в реальных материалах очень часто содержат различные примеси. В условиях переменного внешнего напряжения примесные атомы периодически диффузионным путем перераспределяются между различно ориентированными фасетками. Эффективная толщина границ зависит от концентрации в них примесных атомов. Это приводит к появлению специфического пика внутреннего трения. Аналогичный эффект возникает в нанокристаллическом материале [14, 16, 17] при перераспределении примеси между разными гранями кристаллитов. На основе решения уравнения бародиффузии и использования результатов, приведенных выше, найдено выражение для пика внутреннего трения в этом случае.
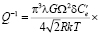
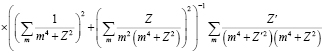. (15)
Здесь
, 
,
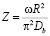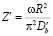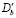– зернограничный коэффициент диффузии примеси, 
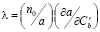– размерный фактор, определяемый из концентрационной зависимости постоянной решетки раствора; 
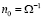– количество атомов матрицы в единице объёма. Концентрация 
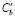определяется как количество примесных атомов на единицу объёма материала границы.
Обсуждение результатов
На рис. 1 приведен график зависимости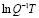 
от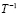 
согласно выражению (7). Он имеет два прямолинейных участка, по-разному наклоненных к оси абсцисс. Это соответствует различным энергиям активации процесса.
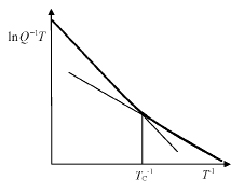
Рис. 1. Температурная зависимость фона ВТ
Такой вид зависимости внутреннего трения можно понять из соображений оценочного характера. Поток вакансий J из сегмента определяется градиентом их концентрации, который пропорционален
,
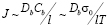где l – диффузионная длина вакансий. Тогда потери ΔW за период колебаний T0 пропорциональны
,
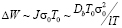упругая энергия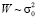 
. Следовательно, 
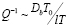. При низких частотах или высоких температурах диффузия успевает пройти на всем сегменте. оэтому за диффузионную длину можно принять его размер L, который от периода колебаний не зависит, тогда 
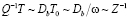. В области высоких частот или низких температур основную роль в диффузионных процессах играют области вблизи границ сегмента протяженностью
.
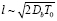В этом случае
.
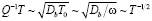Переход от одного участка к другому с разными наклонами не является резким, а происходит в некотором температурном интервале, ширина которого связана с разбросом в размерах фасеток. Оценка их среднего размера дает выражение
.
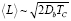Подобная температурно-частотная зависимость характерна для фона внутреннего трения двумерно фасетированных, а также ступенчатых границ.
Температурно-частотная зависимость внутреннего трения F(Z) (множителя в (15), зависящего от Z, пропорционального частоте) для случая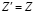 
представлена на рис. 2. В отличие от дебаевского пика изображенный здесь пик несколько несимметричен.
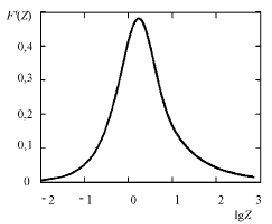
Рис. 2. Пик, связанный с перераспределением примеси
Заключение
В работе рассмотрены основные модели внутреннего трения на границах зерен, имеющих одномерно и двумерно фасетированную структуру. Высокотемпературный фон связан с наличием на фасетках нормальных напряжений и имеет диффузионную природу. На его температурной зависимости имеются области с разными эффективными энергиями активации. Существование пиков внутреннего трения связано с зернограничным проскальзыванием вдоль фасеток или с перераспределением между ними примесных атомов.