science-review.ru
Многосвязная система автоматического управления (МСАУ) – система, в которой одновременно осуществляется регулирование нескольких взаимосвязанных координат. Из-за тесной взаимосвязи между процессами регулирования отдельных координат в таких системах тяжело изучать в полной мере процессы самой системы [1, 2].
Наличие запаздывания в системах автоматического управления усложняет задачу управления объектом, особенно если объект еще и многомерный. Потому что задержка в контуре управления приводит к возрастанию фазового сдвига, которая способна спровоцировать неустойчивость замкнутой системы, в том числе при наличии небольших коэффициентов усиления регулятора [3, 4].
В статье рассматривается линейная многосвязная система автоматического управления, состоящая из множества идентичных (однотипных) сепаратных подсистем и связей через многомерный объект управления. Объектом исследования является МСАУ с запаздыванием со связями через объект управления (рис. 1).
Данная МСАУ представляется с помощью следующих уравнений движения:
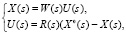(1)
где X0(s), X(s), U(s) – векторы задающих, регулируемых, управляющих воздействий соответственно;
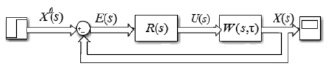
Рис. 1. Структурная схема МСАУ: X0 (s), X(s) – векторы входных и выходных величин; E(s)– единичная матрица; W(s, τ) – передаточная функция; R(s) – МПФ регулятора
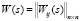– матричная передаточная функция (МПФ) многомерного объекта по управляющим воздействиям, с запаздыванием в перекрестных связях;
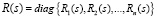– МПФ сепаратных регуляторов [5, 6].
Цель исследования: на основе системного подхода описания МСАУ через характеристики связей и характеристики подсистем предлагается определение устойчивости системы с запаздыванием в перекрестных связях.
Используем подход, где линейная МСАУ рассматривается как множество управляемых подсистем, взаимосвязанных и взаимодействующих друг с другом и образующих единое целое. Данный вид системы можно описать на уровне физических подсистем и многомерных элементов связи между ними, которые рассматриваются в качестве первичных базовых элементов системы [7, 8].
Рассмотрим однотипную МСАУ с запаздыванием в подсистемах. Передаточные функции объекта управления (ОУ) Wij(s) – однотипные, следовательно:
,
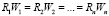где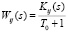 
– матричная передаточная функция многомерного объекта;
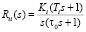– передаточная функция регуляторов с учётом требования астатизма первого порядка по каждому из каналов, равные между собой.
Для МСАУ, соответствующей системе уравнений (1), передаточные функции индивидуальных характеристик подсистем имеют вид [9]:
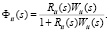(2)
Для полной МСАУ, состоящей из n подсистем и соответствующей системе уравнений (1), характеристика связи (ХС) в общем виде между k подсистемами имеет вид
,
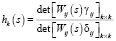где Wij(s) – передаточные функции МСАУ.
; 
.
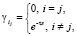
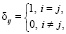
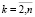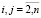Характеристическое уравнение МСАУ в общем виде имеет вид
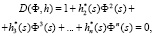(3)
где hk*(s) = hk(s)e-ts, k = 1,…,n.
Проанализируем уравнение связей относительно переменной x:
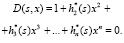(4)
Данное уравнение получается из (3) с помощью подстановки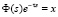 
.
Построив на комплексной плоскости годограф функции Wз(jω) без запаздывания, и корни уравнения (4)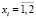 
, можно найти критическое значение τiкр.
Для нахождения критического значения запаздывания tкр необходимо, чтобы годограф Ф(jw), построенный на одной комплексной плоскости с корнями уравнения (3), проходил через ближайший из них и не охватывал при этом другие, то есть МСАУ оказалась на границе устойчивости [10, 11]. Из этого условия получаем систему из двух уравнений относительно t и ω0:
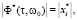
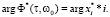(5)
Критическое значение запаздывания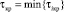 
, 
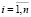– это минимальное из найденных значений ti .
Согласно известному критерию устойчивости для многомерных систем необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики (АФХ) подсистем Ф*(jw,t), для всех w∈(–∞, +∞), построенный на плоскости корней уравнения связи, не охватывал ни один из его корней [11].
Результаты исследования и их обсуждение
Рассмотрим многосвязную САУ с тремя одинаковыми подсистемами, где передаточная функция каждой равна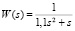 
. Характеристики связей равны h2 = 2,015; h3 = 0,76.
Матричная передаточная функция:
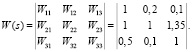
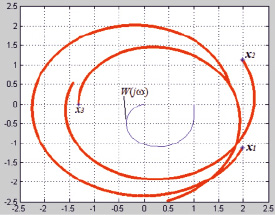
Рис. 2. Годограф МСАУ с запаздыванием в перекрестных связях
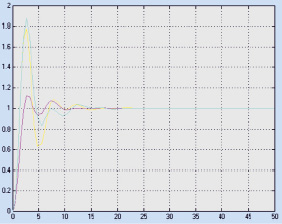
Рис. 3. Переходный процесс МСАУ с запаздыванием в перекрестных связях
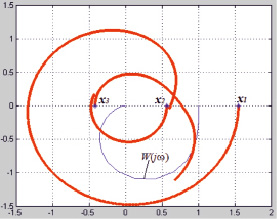
Рис. 4. Годограф МСАУ с запаздыванием в перекрестных связях
Добавив запаздывание в перекрестные связи, получаем
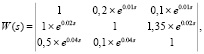
где t1 = 0,02; t2 = 0,05; t3 = 0,07.
Характеристическое уравнение связи для САУ с тремя подсистемами равно
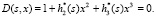(6)
Корни характеристического уравнения связи (6) при w = 0 равны:
x1,2 = 1,9864 ± 1,1352i;
x3 = –1,3176 + 0,0000i.
Так как корни характеристического уравнения не пересекают годограф W(jw), следовательно, система устойчива (рис. 2). Эффективность подхода подтверждена с помощью моделирования (рис. 3) [12, 13].
Поскольку колебания затухают, следовательно, это свидетельствует об устойчивости трехсвязной МСАУ при данных значениях запаздываний.
Повлиять на устойчивость системы можно не только с помощью других значений t, но и изменив коэффициенты перекрестных связей.
Рассмотрим ту же замкнутую САУ с тремя одинаковыми подсистемами, где передаточная функция каждой равна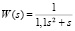 
. Характеристики связей равны h2 = 4,23; h3 = –0,914.
Матричная передаточная функция:
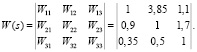
Добавив запаздывание в перекрестные связи, получаем
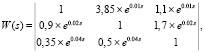
где t1 = 0,02; t2 = 0,05; t3 = 0,07.
Корни характеристического уравнения связей (6) при w = 0 равны
x1 = 1,5348;
x2 = 0,5658;
x3 = –0,4134.
Так как один корень характеристического уравнения находится в области годографа W(jw), следовательно, система неустойчива (рис. 4).
Эффективность подхода подтверждена с помощью моделирования (рис. 5), где видно, что система выходит из состояния равновесия в неустойчивое [13].
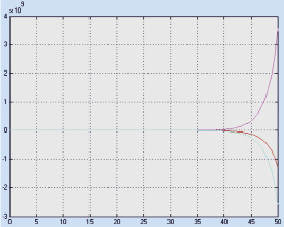
Рис. 5. Переходный процесс МСАУ с запаздыванием в перекрестных связях
Заключение
В работе предложен метод декомпозиции, который позволяет с помощью описания МСАУ через характеристики связей и характеристики подсистем определить устойчивость МСАУ с запаздыванием. Также рассмотрен способ нахождения критического значения запаздывания для многосвязных систем. Правильность результатов подтверждена с помощью моделирования МСАУ с запаздыванием в перекрестных связях.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (Гранты РФФИ №18-08-00702 А, 18-08-01299 А).