Получившая в последнее время широкую известность задача «Извлечение знаний» (англ.: data mining) формулируется так [1, 2]. Имеется достаточно объемный банк данных, в котором, как предполагается, присутствуют априори не известные, не тривиальные, практически значимые и интерпретируемые в предметной области закономерности, которые необходимо сформулировать явно. К такой постановке относится большое число задач бизнеса, науки, технологии. Все они имеет практическую значимость, так как в условиях конкуренции их решение может привести к дополнительным технологическим, научным или конкурентным преимуществам. Понятно, что используемые термины носят достаточно нечеткий характер. Так под неизвестными закономерностями понимаются новые, а не сведения, подтверждающие уже полученные. Нетривиальные – которые нельзя просто обнаружить при непосредственном визуальном анализе данных или вычислении простых статистических характеристик. Практическую значимость уточнить затруднительно, поэтому полагаем, что этот термин базируется на здравом смысле [3].
Разнообразие методов извлечения знаний в настоящее время весьма значительно. Каждый из них базируется на определенной методике и применим в той или иной конкретной ПО при решении тех или иных задач. В этой статье приводится еще одно решение упомянутой задачи, которое может оказаться практически значимым в случаях, как представляется, неполного определения предметной области (ПО), когда имеется предположение, что множество имеющихся данных может быть расширено за счет новых.
Вначале сформулируем, как на содержательном уровне понимается задача определения закономерностей по имеющемуся набору данных. Пусть имеется некоторая совокупность данных, назовем их экспериментальными, которая относится к определенной ПО. Каждое их них представляет собой некоторый объект ПО, который удалось наблюдать, например, в результате экспериментов. И для этих данных необходимо установить описывающую их закономерность. Здесь задача установления закономерности понимается как возможность предсказать, какие еще объекты ПО могут возникнуть и какие нет. Конечно, вопрос о наличии новых объектов решается с некоторой неопределенностью, так как имеющиеся данные могут быть неполными, что может повлечь ошибку предсказания. Предсказание может осуществляться на основе различных критериев, дающих разные результаты. В этой статье мы рассмотрим предсказание на основе так называемого отношения ортогональности признаков, которыми характеризуются объекты ПО.
Цель статьи состоит в том, чтобы описать метод предсказания существования новых данных ПО, основываясь на имеющихся экспериментальных данных. Кроме того, в статье устанавливается, какое количество новых объектов может содержать ПО в зависимости от мощности множества экспериментальных данных.
Описание данных графами ортогональности
Теперь изложим те же соображения формально. Пусть имеется множество P независимых признаков, в терминах которых описываются объекты ПО. Каждый объект характеризуется подмножеством O ⊆ P признаков. Количество признаков у объекта не фиксировано, и они никак не упорядочены. Пусть O есть множество объектов, которые составляют подмножество всевозможных объектов ПО. Назовем эту совокупность – экспериментальными данными. В экспериментальных данных нас интересуют лишь нетривиальные объекты, т.е. содержащие не менее двух признаков. Задача состоит в том, чтобы, основываясь на имеющейся совокупности O, для множества O' ⊆ P признаков установить, может ли оно представлять некоторый объект ПО. Тем самым задачу извлечения знаний мы понимаем как построение объектов, наличие которых в ПО логически следует из экспериментальных данных.
Будем исходить из допущения полноты экспериментальных данных: если два признака p1, p2 ∈ P не встречаются одновременно в одном объекте из O, то они не встречаются одновременно ни в одном объекте ПО. Такие признаки назовем ортогональными. В противном случае, если они принадлежат хотя бы одному экспериментальному объекту, – совместимыми. То есть любые совместимые признаки p1, p2 ∈ P обязательно встречаются хотя бы в одном экспериментальном объекте.
Используемая нами гипотеза для предсказания принадлежности нового объекта ПО состоит в следующем: объект представляется всяким подмножеством признаков, среди которых нет ни одной пары ортогональных. Ее назовем 2-гипотезой, так как она касается вхождения в один объект пары неортогональных признаков, и чтобы отличать ее от других гипотез, которые будут сформулированы далее. Таким образом, никакая пара ортогональных признаков не может входить в описание объекта рассматриваемой ПО.
Построим по совокупности O экспериментальных данных граф GO ортогональности: его узлами являются признаки множества P поименованные также, два узла смежные в том случае, если соответствующие признаки ортогональные [4]. Очевидна следующая теорема.
Теорема 1. Каждому объекту экспериментальных данных O в графе GO ортогональности соответствует пустой подграф.
Однако не каждому пустому подграфу соответствует объект в множестве O экспериментальных данных. Может сложиться ситуация, когда нетривиальный пустой подграф графа ортогональности не определяет объекта из экспериментальных данных. Если пустой подграф E ⊆ GO не определяет объекта, принадлежащего экспериментальным данным, то назовем совокупность узлов этого подграфа – потенциальным объектом. Покажем, что наличие потенциального объекта в предметной области не противоречит 2-гипотезе.
Введем следующее определение.
Пусть GO есть граф ортогональности с множеством P узлов. Базисом для GO назовем множество максимальных пустых подграфов, полностью определяющих отношение смежности узлов в GO. Очевидно, что подграфы базиса графа GO покрывают все узлы множества P. Базис называется не избыточным, если из него нельзя выбросить ни одного пустого подграфа без нарушения свойства быть базисом.
Базисы графа ортогональности имеют непосредственное отношение к имеющимся экспериментальным данным. Экспериментальные объекты в совокупности определяют несколько неизбыточных базисов графа ортогональности. Если экспериментальные данные определяют совокупность E базисов построенного графа ортогональности, то заключение о принадлежности ПО нового объекта, не содержащегося в экспериментальных данных, вытекает из допущения, что совокупность E включает базис для графа ортогональности, который можно построить по всей ПО, а не только по экспериментальным данным. А так как базис однозначно определяет граф, то построенный граф GO и есть граф ортогональности для всей ПО. Тем самым закономерности экспериментальных данных распространяются на все ПО. На этом основывается предсказание наличия в ПО объектов, которых нет среди экспериментальных.
Пример 1. Рассмотрим совокупность экспериментальных данных O = {ac, bd, ad, ef} над множеством признаков {a, b, c, d, e, f}. Построенный по совокупности O граф ортогональности GO выглядит как на рисунке. В нем пунктиром выделены все пустые подграфы, определяемые экспериментальными данными. Нетрудно увидеть, что они образуют (избыточный) базис. Возникает вопрос: за счет каких объектов можно расширить множество O, не вызывая противоречия с 2-гипотезой. Присутствие новых объектов ПО должно логически следовать из имеющихся экспериментальных данных и 2-гипотезы.
В графе GO можно отметить следующие нетривиальные максимальные пустые подграфы, которые не вошли в приведенный базис: af, bfe. Таким образом, в соответствии с 2-гипотезой, ПО может быть пополнена включением в нее двух новых объектов af, bfe. И такое пополнение является следствием экспериментальных данных и 2-гипотезы. В свою очередь 2-гипотеза есть следствие того, что экспериментальные данные обладают свойством полноты, т.е. содержат все соотношения ортогональности признаков, которые наличествуют в ПО.
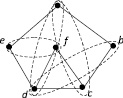
Граф ортогональности с выделенным базисом
О числе новых объектов, определяемых экспериментальными данными
Естественно возникает желание оценить число новых объектов ПО, которые не являются экспериментальными, но могут быть включены в ПО, основываясь на 2-гипотезе. Здесь будем рассматривать те объекты, которые определяются максимальными нетривиальными пустыми подграфами графа ортогональности, построенного по экспериментальным данным. Понятно, что, решив задачу в такой постановке, без труда удается причислить к ПО и объекты с меньшим числом признаков, соответствующие не максимальным пустым подграфам.
Введем такое определение. Пусть каждый узел из подграфа E1 совпадает или смежный с некоторым узлом из E2. В этом случае говорим, что подграф E1 смежный с E2. Очевидно, что граф E2 может не быть смежным с E1. То есть такое отношение смежности несимметрично. Поэтому потребует, что каждый узел из E2 совпадает или смежный с некоторым узлом из E1. В этом случае говорим, что пара графов E1 и E2 смежная, а все ребра инцидентные одновременно узлам E1 и E2 назовем их ребрами смежности. Такое отношение смежности симметрично.
Очевидны следующие утверждения.
Теорема 2. Если B есть базис графа G, то каждая пара его подграфов смежная. Для любых узлов v1, v2 графа G и всякого его базиса B либо они принадлежат одному подграфу этого базиса, либо разным подграфам, и тогда они соединены ребром. Пусть {E1, E2, …, Eq} есть не избыточный базис. Тогда любой подграф Ei , i ∈ {1, 2, …, q} не покрывается остальными подграфами базиса.
Если E1 и E2 суть максимальные, нетривиальные пустые подграфы графа ортогональности, то они смежные. Содержательно это понимается так: подграфы E1 и E2 определяют разные объекты, которые разделяются хотя бы одной парой ортогональных признаков. Хотя остальные признаки этих объектов могут совпадать.
Так как в неизбыточном базисе {E1, E2, …, Eq} каждый граф содержит хотя бы один узел, который не содержится во всех остальных, то при рассмотрении неизбыточных базисов можно ограничиться базисами с числом подграфов не более n, где n – число узлов.
Известно, что всякая матрица смежности размера n×n описывает не менее чем 2(n-1)2/2n! различных не изоморфных графов с n узлами.
Каждое подмножество P' ⊆ P узлов графа, где n = |P|, определяет максимальный пустой подграф, узлы которого образуют множество P'. Тогда во всех графах с n узлами число различных максимальных пустых подграфов равно 2n.
Так как разные графы имеют несовпадающие базисы, то, если из произвольного графа G удалить или добавить ребро, в результирующем графе G' ни один базис не совпадает ни с одним базисом графа G. Отсюда следует такое утверждение.
Теорема 3. Почти каждый граф с n узлами обладает неизбыточным базисом, мощность которого по порядку равна n.
Доказательство. Будем порождать все графы числом 2(n-1)2/2n! = 2с1n2, определяя для каждого неизбыточный базис. Для первого элемента базиса подходит один из 2n максимальных пустых подграфов. Для второго 2n – 1, и т.д. Для того, чтобы таким способом породить все 2с1n2 графов с n узлами, нам потребуется выбрать порядка n элементов базиса. Отсюда следует, что почти каждый граф с n узлами обладает неизбыточным базисом мощности порядка n.
Теорема доказана.
Таким образом, если принять 2-гипотезу, то n = |P| объектов могут определить все объекты ПО, которые можно описать в терминах признаков P. Для этого достаточно найти неизбыточный базис, который определяет граф ортогональности. И затем по построенному графу ортогональности построить все объекты ПО, определяемые максимальными пустыми подграфами.
Естественно возникает вопрос, сколько объектов может быть в ПО, чтобы определяемый ею граф ортогональности совпадал с графом ортогональности, построенным по экспериментальным данным. Как мы показали, нахождение пустых подграфов в произвольных графах имеет немалое прикладное значение в плане извлечения новых знаний. В связи с этим интерес представляет такое утверждение.
Теорема 4. Существует граф ортогональности с n узлами, в котором имеется не менее 2сn пустых подграфов, где c – некоторая положительная константа.
Построение такого графа ортогональности основывается на так называемых графах-расширителях, которые характеризуются следующим свойством [5]. Для каждого подграфа с m узлами в графе расширителе его граница имеет число ребер, сравнимое с m. Это свойство расширителей позволяет строить сложные объекты, по сравнительно простым спецификациям. В частности, удается построить логические выводы и множества единичных означиваний экспоненциальной сложности от длины логических формул.
Таким образом, если экспериментальные данные определяют базис графа ортогональности всей ПО, то в некоторых случаях они могут быть расширены за счет новых объектов, число которых определяется экспонентой от числа признаков, в которых описываются объекты. И тогда получаем, что информация, представленная в экспериментальных данных, при принятии 2-гипотезы, оказывается достаточной, чтобы построить весьма объемную предметную область.
N-гипотеза
Однако возможна ситуация, когда из множества n ≥ 3 признаков каждые n – 1 попарно совместимые, но все n не встречаются ни в одном объекте из экспериментальных данных O. В этом случае 2-гипотеза оказывается слабой, чтобы только на ее основании прогнозировать наличие объектов в ПО, которых нет в экспериментальных данных. В этом случае необходимо усилить эту гипотезу до n-гипотезы, которая запрещает в отдельных случаях одновременное вхождение n признаков. Для конкретности, будем рассматривать ситуацию, когда n = 3 и следующим образом формулируем 3-гипотезу. Случаи, когда n > 3, восстанавливаются аналогично.
Пусть признаки a, b, c попарно не ортогональные, однако в экспериментальных данных не встречаются одновременно в представлении ни одного объекта. Если обозначить A высказывание: «признак a встречается в описании объекта O», B: «признак b встречается в описании объекта O», C: «признак c встречается в описании объекта O», то высказывание «признаки a, b, c не встречаются одновременно в описании одного объекта» представляется формулой: F3(A, B, C) = A(B⊕C) ∨ B(A⊕C) ∨ C(A⊕B). Действительно, если признак a встречается в описании объекта, то признаки b и c не могут встретиться в его описании одновременно. Аналогично для двух других признаков b, c. Тривиальный случай, когда ни один из признаков не встречается в описании объекта, не рассматривается, как не представляющий интереса. Для случаев большего числа признаков подобный критерий строится рекурсивно. Следует отметить, что установление выполнимости этой и подобных ей формул для большего числа признаков осуществляется проверкой на пустых подграфах графа ортогональности и поэтому не требует большого перебора.
Тогда 3-гипотеза выглядит так: если для попарно не ортогональных признаков a, b, c верно, что они не встречаются в представлениях ни одного объекта экспериментальных данных, то они не встречаются в представлении ни одного объекта ПО. Для того, чтобы удостовериться в верности этой гипотезы для всякого набора признаков, необходимо удостовериться в ее истинности для каждой тройки признаков из множеств, определяемых пустыми подграфами графа ортогональности GO.
Таким образом, проверка 2-гипотезы сводится к проверке совместимости троек признаков из максимальных пустых подграфов графа ортогональности.
Заключение
Решена задача предсказания принадлежности объектов предметной области в соответствии с так называемой n-гипотезой (n ≥ 2). Последняя предполагает, что экспериментальные данные, в которых осуществляется поиск закономерностей, позволяют сделать вывод о совместимости признаков объектов во всей предметной области. Тем самым логически обосновывается наличие объектов, которых нет в экспериментальных данных, но добавление которых не противоречит им.


 science-review.ru
science-review.ru