I. Моделирование кривых и поверхностей
В начертательной геометрии моделирование поверхности решается прямой задачей: по данным поверхности и аппарату проецирования получить модель поверхности на плоскости, а решение обратной задачи – конструирование поверхности решается следующим образом: по данным модели и аппарату проецирования сконструировать поверхность. При решении прямой и обратной задач вид и тип модели и поверхности зависит от взаимного расположения аппарата проецирования относительно поверхности или модели.
Так как свойства поверхности во многом определяются свойствами ее линий, поэтому моделирование и конструирование кривых представляет важную компоненту сложных задач моделирования и конструирования поверхностей.
В методе двух изображений, при проецировании двумя пучками прямых, только плоскость и поверхности моноидального типа Σn с двумя и более (n-1) – кратными точками, в две из которых помещаются центры проецирования, моделируются на плоскости изображений взаимно однозначными соответствиями. Остальные поверхности моделируются на плоскости проекций многозначными соответствиями. Многозначные соответствия сложны, значит изучение свойств поверхностей, инцидентных ей линий, особых точек и т.д. затруднено. Поэтому в начертательной геометрии возникает актуальная задача проецирования подбором аппарата отображения получать в качестве модели поверхности или кривых взаимно однозначные соответствия. При конструировании поверхностей на уровне заданных моделей можно прогнозировать их тип и вид, а при конструировании двух поверхностей прогнозировать тип их пересечения, касание определенного порядка гладкости.
I. 1. Анализ методов изображений в начертательной геометрии
Одна из главных задач начертательной геометрии заключается в исследовании взаимосвязи характеристик моделируемого пространства, имеющего ту или иную размерность и структуру, модели, аппарата отображения и носителя моделей.
При геометрическом моделировании в n-мерном пространстве размерность оригинала, характеристики аппарата отображения и изображения связаны с размерностью операционного пространства, в качестве которого обычно принимают расширенное евклидово n-мерное пространство Еn.
Оригиналом в Еn может быть линейное или нелинейной подпространство размерности k, Kk , где 0£ k < n-1.
В качестве основного элемента пространства рассматривают линейные или нелинейные подпространства  размерности
размерности  , где
, где 
Аппарат отображения может состоять из проецирующих линейных или нелинейных многообразий Mm размерности  где
где 
Изображение строится на носители модели, являющимся линейным или нелинейным подпространством  размерности
размерности  где
где 
Моделью основного элемента оригинала может являться линейное или нелинейное подпространство  размерности
размерности  где
где 
Впредь в качестве операционного пространства будем рассматривать трехмерное пространство E3 в котором оригиналом может быть поверхность (плоскость), кривая (прямая), точка, то есть  а основным элементом оригинала может выступать кривая линия (прямая) или точка, то есть t = 0,1.
а основным элементом оригинала может выступать кривая линия (прямая) или точка, то есть t = 0,1.
В качестве аппарата проецирования можно использовать многообразия поверхностей (плоскостей), кривых линий (прямых), то есть  Носителем моделей может быть трехмерное пространство, поверхность (плоскость), кривая линия (прямая), то есть
Носителем моделей может быть трехмерное пространство, поверхность (плоскость), кривая линия (прямая), то есть 
Основной элемент может моделироваться плоской кривой линией (циклография, одноосевое проецирование), парами, тройками и т. д. точками, значит 
Моделью оригинала в зависимости от аппарата проецирования может быть линейное или нелинейное многообразие точек, линий.
На практике размерность  отображаемого пространства больше размерности носителя модели. Однако есть примеры, когда пространство меньшей размерности отображается на пространство большей размерности [1].
отображаемого пространства больше размерности носителя модели. Однако есть примеры, когда пространство меньшей размерности отображается на пространство большей размерности [1].
В процессе отображения участвуют:
- оригинал,
- аппарат отображения,
- модель (изображение),
- носитель модели.
В начертательной геометрии трехмерного пространства рассматриваются оригиналы, образованные или из множества точек, или из множества прямых. Отсюда возникают два подхода моделирования:
- метод двух изображений,
- метод двух следов.
Метод двух следов применяется при моделировании линейчатых пространств, где основным элементом является прямая. На практике распространение получил метод двух изображений, который применяется при моделировании точечного пространства. В результате применения классических методов двух изображений и двух следов модели получаются линейными.
Построение моделей точечного пространства начинается естественно, с отображения точки. Ее можно изображать либо каким-то одним геометрическим элементом (например, в циклографии точка пространства моделируется кривой линией на плоскости изображений), либо двумя (например, в методе Монжа – парой точек), тремя и т.д. геометрическими элементами. Когда точка моделируется одним геометрическим элементом, модель называется моно моделью, когда двумя – бинарной моделью, тремя – тернарной, четырьмя – кватернарной и т.д. В результате моделирования элементам оригинала сопоставляются элементы модели. В зависимости от сопоставления различают следующие способы моделирования:
- аксиоматический,
- конструктивный,
- аналитический.
Аксиоматический способ моделирования основан на параметрическом исчислении. При аксиоматическом способе моделирования оригинал не связан непосредственно с моделью. Модель, получаемая таким способом, называется независимой.
При конструктивном способе моделирования оригинал и модель связаны проецирующим аппаратом, модели, получаемые таким конструктивным способом, называются зависимыми. В основе всякого конструктивного способа отображения ряда пространственных объектов на плоскость лежит определенная теория преобразования плоскости проекций, позволяющая изучать свойства и расположения пространственных объектов по полученным моделям. Если линейные методы отображения основаны в общем случае на теории проективных преобразований, то нелинейные методы – главным образом на теории нелинейных преобразований, которые называются кремоновыми многозначными соответствиями [2]. Наличие конструктивной взаимосвязи пространства и его модели позволяет изучать свойства оригиналов по их моделях. Вся совокупность моделей, подлежащих систематизации, может дать цельную картину взаимосвязей между моделями, упорядочить имеющиеся методы изображений и позволят осуществить направленный поиск моделей с наперед заданными свойствами для тех или иных областей приложений.
При аналитическом способе моделирования оригинал и модель связаны аналитической зависимостью. Результаты такого моделирования являются числа, уравнения и пр. Аналитический способ моделирования широко применяется в математическом моделировании.
В начертательной геометрии применяются аксиоматический и конструктивные способы моделирования.
Наряду с линейными моделями существуют нелинейные модели, которые получаются:
- при замене центрального проецирования проецированием конгруэнциями или комплексами кривых (прямых);
- при проецировании поверхностями (плоскостями);
- при замене плоскости проекций поверхностями или кривыми.
I. 2. Систематизация аппаратов отображения и носителей моделей
До середины 18-го века проецирование оригинала выполнялось одной или двумя связками прямых на одну плоскость и редко на сферу и цилиндрическую поверхность (купольная и панорамные перспективы). Развитие науки и техники потребовало исследование проецирования объектов любой размерности и структуры на различные носители, для чего потребовалось использовать в качестве аппарата проецирования геометрические многообразия различных размерностей. Рассмотрим детально эти вопросы для трехмерного пространства и дадим систематизации аппаратов проецирования и носителей моделей.
В качестве аппарата отображения в конструктивном способе проецирования целесообразно использовать проецирующие многообразия, позволяющие через точку пространства проводить лишь один элемент многообразия, или другими словами, произвольная точка пространства выделяет из данного проецирующего многообразия только один элемент многообразия.
Подсчетом параметров, исходя из требования инцидентности произвольной точке пространства конечного числа проецирующих элементов, можно показать, что в качестве проецирующих многообразий для моделирования трехмерного точечного пространства можно использовать:
- одномерные многообразия (кривые линии, в частном случае, прямые);
- двумерные многообразия (поверхности, в частном случае, плоскости).
Так, например, аппарат отображения, используемый в методе двух следов и двух изображений, состоят из связок прямых, то есть двупараметрического множества прямых пространства, которое позволяет точке пространства выделить из связки прямых только одну прямую.
I. 3. Многообразие прямых
В пространстве E3 прямых ∞4. Подмножества этого многообразия суть ∞1,∞2, ∞3, которые соответственно называются:
- однопараметрическими,
- двупараметрическими,
- трехпараметрическими множествами прямых.
Однопараметрические множества прямых образуют:
- семейство касательных прямых к плоской кривой (рис. 1),
- пучок прямых (множество прямых плоскости, инцидентных одной точке) (рис. 2),
- образующие линейчатой поверхности.

Рис. 1

Рис. 2
Двупараметрическим множеством прямых называется конгруэнция прямых и обозначается Kг(n, k).
Трехпараметрическим множеством прямых называется комплекс Km(n) прямых.
Для отображения точечного трехмерного пространства необходимы двупараметрические и трехпараметрические одномерные многообразия.
В самом общем случае конгруэнцию прямых образуют общие касательные прямые к двум поверхностям или двойные касательные прямые к одной поверхности. Эти поверхности называются фокальными поверхностями, а точки касания прямых конгруэнции с ними называют фокусами этих прямых.
Если каждый луч системы касается фокальной поверхности дважды; в соответствии с этим различаются две «полости» фокальной поверхности.
Если фокальные поверхности заменить пространственными кривыми линиями  и
и  , то конгруэнция прямых будет состоять из прямых
, то конгруэнция прямых будет состоять из прямых  , пересекающих обе фокальные кривые линии, или из бисекант
, пересекающих обе фокальные кривые линии, или из бисекант  одной пространственной линии
одной пространственной линии  (рис. 3).
(рис. 3).

Рис. 3
Известно [3], что существуют различные способы задания конгруэнции прямых. Конгруэнции прямых Кг ( характеризуются порядком
характеризуются порядком  и классом
и классом  . Порядок
. Порядок  конгруэнции равен числу прямых конгруэнций, проходящих через произвольную точку пространства. Класс k конгруэнции равен числу прямых конгруэнций, принадлежащих произвольной плоскости пространства.
конгруэнции равен числу прямых конгруэнций, проходящих через произвольную точку пространства. Класс k конгруэнции равен числу прямых конгруэнций, принадлежащих произвольной плоскости пространства.
Из многих способов задания конгруэнций прямых наиболее подходящим применительно к моделированию поверхностей является способ, в котором конгруэнция прямых определяется как множество прямых, пересекающих данные  и
и  кривые линии (рис. 4).
кривые линии (рис. 4).

Рис. 4
Если кривые линии  и b алгебраические соответственно порядков n1 и n2, не имеющие общих точек, то они определяют дуальную конгруэнцию Kг(n, n) прямых, у которой порядок и класс равны между собой, то есть n = n1 × n2 = k.
и b алгебраические соответственно порядков n1 и n2, не имеющие общих точек, то они определяют дуальную конгруэнцию Kг(n, n) прямых, у которой порядок и класс равны между собой, то есть n = n1 × n2 = k.
В качестве аппарата проецирования целесообразно использовать конгруэнции прямых первого порядка Kг (1, k), чтобы через точку пространства проходила единственная проецирующая прямая данной конгруэнции. Конгруэнция прямых Kг(1,k), задается фокальной прямой  и пространственной фокальной кривой линией bk порядка k, имеющей с прямой
и пространственной фокальной кривой линией bk порядка k, имеющей с прямой  (k-1) – фиксированных общих точек (рис. 5).
(k-1) – фиксированных общих точек (рис. 5).

Рис. 5
Частным случаем конгруэнции прямых Kг(1, k) является конгруэнция прямых первого класса Kг (1, 1), которая может быть гиперболической, эллиптической и параболической. Эти конгруэнции получаются, когда фокальными линиями конгруэнции прямых являются прямыми:
- если прямые фокальные конгруэнции являются скрещивающимися действительными прямыми, то конгруэнция прямых будет гиперболической (рис. 6);

Рис. 6
- если фокальные прямые конгруэнции мнимые прямые – эллиптической;
- если фокальные прямые совпадут, то конгруэнция прямых будет параболической. В пределе, когда фокальные прямые пересекутся, конгруэнция Kг(1,1) прямых распадется на связку Кг (1,0) (множество прямых пространства, инцидентных общей точке) прямых (рис. 7) и плоское поле прямых Кг (0,1) (рис.8).
Кг (1,1)=Кг (1,0)+Кг (0,1).

Рис. 7

Рис. 8
Как известно, через произвольную точку P пространства E3проходит ∞1 прямых данного комплекса. Они образуют конус, который называется конусом комплекса с вершиной P. Каждый комплекс характеризуется степенью. Степень комплекса определяется порядком конической поверхности, выделяемой из комплекса произвольной точкой P (рис. 9).

Рис. 9
Из ∞4 множества прямых пространства можно выделить комплекс прямых многими способами:
- множество прямых, пересекающих пространственную кривую линию  . Частным случаем такого комплекса прямых является комплекс Kм (1), когда
. Частным случаем такого комплекса прямых является комплекс Kм (1), когда  прямая. Множество прямых такого типа образуют трехпараметрическое множество прямых, так как точек на кривой ∞1, а каждая точка выделяет в пространстве связку (∞ 2) прямых. Значит, всего прямых комплекса будет ∞3;
прямая. Множество прямых такого типа образуют трехпараметрическое множество прямых, так как точек на кривой ∞1, а каждая точка выделяет в пространстве связку (∞ 2) прямых. Значит, всего прямых комплекса будет ∞3;
- множество прямых, касающихся поверхности;
- множество прямых, соединяющих соответственные точки кремонова преобразования пространства (ассоциированный комплекс преобразования), [4].
I. 3. Многообразие кривых
Многообразия кривых линий трехмерного пространства весьма обширны и не подлежат, по-видимому, строгой систематизации.
Нас интересуют лишь двумерные многообразия плоских алгебраических кривых линий, которые будут нами использованы в качестве проецирующих линий обобщенного аппарата проецирования, то здесь приведем лишь примеры конгруэнций и комплексов кривых линий:
1. Семейство окружностей, инцидентных пучку ( ) плоскостей αi. Инцидентных точке Ai и точке Ai, получаемой как пересечение пространственной кривой линии
) плоскостей αi. Инцидентных точке Ai и точке Ai, получаемой как пересечение пространственной кривой линии  порядка n с плоскостью a i пучка плоскостей (
порядка n с плоскостью a i пучка плоскостей ( ) . Для кривой линии
) . Для кривой линии  порядка n ось
порядка n ось  пучка плоскостей
пучка плоскостей  является (n-1) – секантой. То есть кривая линия
является (n-1) – секантой. То есть кривая линия  порядка n, будет иметь (n-1) пересечений с прямой
порядка n, будет иметь (n-1) пересечений с прямой  и только одно пересечение с плоскостью αi пучка плоскостей. Такое семейство окружностей двупараметрично: окружностей, проходящих через две фиксированные точки Ai и P – ∞1, а плоскостей в пучке (
и только одно пересечение с плоскостью αi пучка плоскостей. Такое семейство окружностей двупараметрично: окружностей, проходящих через две фиксированные точки Ai и P – ∞1, а плоскостей в пучке ( ) – ∞1, значит ∞1 × ∞1 = ∞2, (рис. 10).
) – ∞1, значит ∞1 × ∞1 = ∞2, (рис. 10).

Рис. 10
2. Семейство коник, принадлежащих пучку ( ) плоскостей и пересекающих в двух точках каждую из пространственных кривых линий
) плоскостей и пересекающих в двух точках каждую из пространственных кривых линий  и bn порядков n , для которых ось
и bn порядков n , для которых ось  пучка плоскостей является (n-2) – секантой, таких коник будет – ∞2, плоскоcтей в пучке (
пучка плоскостей является (n-2) – секантой, таких коник будет – ∞2, плоскоcтей в пучке ( ) – ∞1, коник, инцидентных 4-ем фиксированным точкам A,B,C,D – ∞1 (рис. 11) и т. д. В плоскости
) – ∞1, коник, инцидентных 4-ем фиксированным точкам A,B,C,D – ∞1 (рис. 11) и т. д. В плоскости  лежит коника
лежит коника  .
.

Рис. 11
Как говорилось выше, коник на плоскости ∞5, то есть коника определяется на плоскости, например, 5-ю точками, окружности – множество коник плоскости инцидентных двум общим циклическим точкам, поэтому окружностей на плоскости – ∞3, то есть окружность на плоскости можно определить, например, 3-мя точками, или центром окружности – ∞2 и величиной радиуса окружности – ∞1 и т.д.
В качестве проецирующих линий можно использовать не только кривые линии второго порядка, но и плоские кривые линии высших порядков. Кривых линий 3-го порядка на плоскости ∞9, кривых линий 4-го порядка – ∞14, кривых линий n-го порядка на плоскости – 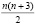 параметрическое множество. Закрепив в плоскости пучка (
параметрическое множество. Закрепив в плоскости пучка ( ) плоскостей соответственно 8, 13,
) плоскостей соответственно 8, 13, 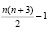 – точек, будем получать ∞1 кривых линий соответственно третьего, четвертого, n-го порядков, то множество этих кривых в пучке плоскостей будет двупараметрическим.
– точек, будем получать ∞1 кривых линий соответственно третьего, четвертого, n-го порядков, то множество этих кривых в пучке плоскостей будет двупараметрическим.
Элементами комплекса линий могут быть также плоские кривые линии. Например, семейство окружностей, принадлежащих пучку ( ) плоскостей и проходящих через общую точку P ∈
) плоскостей и проходящих через общую точку P ∈  (рис.12). Это семейство окружностей трехпараметрическое множество, так как на плоскости окружностей, инцидентных одной точке P – ∞2 , плоскостей в пучке (
(рис.12). Это семейство окружностей трехпараметрическое множество, так как на плоскости окружностей, инцидентных одной точке P – ∞2 , плоскостей в пучке ( ) – ∞1, и т. д. Аналогично рассуждая, можно показать принципиальную возможность применения в качестве аппарата проецирования пространственных кривых линий. Например, конгруэнций пространственных кривых линий третьего порядка (нормкривых) можно задать пятью точками. Нормкривая однозначно определяется 6-ю точками (12 параметров). Чтобы получить двупараметрическое множество нормкривых, необходимо закрепить 10 параметров, например, 5 точек на какой-либо поверхности и т.д.
) – ∞1, и т. д. Аналогично рассуждая, можно показать принципиальную возможность применения в качестве аппарата проецирования пространственных кривых линий. Например, конгруэнций пространственных кривых линий третьего порядка (нормкривых) можно задать пятью точками. Нормкривая однозначно определяется 6-ю точками (12 параметров). Чтобы получить двупараметрическое множество нормкривых, необходимо закрепить 10 параметров, например, 5 точек на какой-либо поверхности и т.д.

Рис. 12
I. 4. Проецирующие плоскости и поверхности
Исчислением параметров можно показать, что множество проецирующих плоскостей и поверхностей при моделировании точечного пространства могут быть одно -, дву- и трехпараметрическими. В первом случае поверхность (плоскость) является проецирующей для всех своих точек, например, известное «осевое проецирование» [5]. Во втором случае каждая проецирующая поверхность является проецирующей для каждых ∞1 своих точек, например, точек принадлежащих одной образующей. В третьем случае через каждую точку пространства проходит своя проецирующая поверхность, след которой на плоскости проекций будет изображением этой точки. Очевидно, по этой схеме получаются циклографические модели.
Как в случае проецирования многообразиями кривых линий (прямых), здесь возможны многочисленные варианты задания проецирующих поверхностей (плоскостей). Например, однопараметрическое множество (пучок) плоскостей составляют:
- множество плоскостей  , инцидентных фиксированной прямой
, инцидентных фиксированной прямой  , которая называется осью пучка плоскостей. Она пересекает некоторую плоскость
, которая называется осью пучка плоскостей. Она пересекает некоторую плоскость  , не принадлежащую пучку
, не принадлежащую пучку  плоскостей, в точке
плоскостей, в точке  , а каждая плоскость пучка
, а каждая плоскость пучка  плоскостей пересекает плоскость
плоскостей пересекает плоскость  по прямой, которые в плоскости П образуют пучок
по прямой, которые в плоскости П образуют пучок  прямых
прямых  (рис. 13);
(рис. 13);
- множество плоскостей, касающихся, в общем случае, торсовой поверхности.

Рис. 13
Приведем также примеры пучков поверхностей:
- множество сфер, инцидентных фиксированной окружности;
- множество сфер, пересекающих прямую в двух фиксированных точках и касающихся данной плоскости и т.д.
Указанные множества являются однопараметрическими. Так в первом случае множество плоскостей, инцидентных прямой, имеют один свободный параметр, т.е. их – ∞1. Во втором случае сфер в пространстве ∞4 условие инцидентности фиксированной окружности требует затраты трех параметров, значит, у всех сфер данного пучка остается один свободный параметр. В третьем случае, пересечение множества сфер с прямой в двух фиксированных точках закрепляет два параметра, касание плоскости сферами – один параметр, остается свободным один параметр.
Примерами двупараметрического семейства поверхностей является связка плоскостей (рис. 14), выполненный на основе рис. 7 для демонстрации связи связки (S) прямых и связки (S) плоскостей пространства.
Т. к. пересечение плоскости, например  , не проходящей через точку S, со связкой (S) прямых получаем плоское поле точек, а пересечение ее со связкой (S) плоскостей получаем плоское поле прямых; множество плоскостей, касающихся не развертывающейся поверхности и т. д.
, не проходящей через точку S, со связкой (S) прямых получаем плоское поле точек, а пересечение ее со связкой (S) плоскостей получаем плоское поле прямых; множество плоскостей, касающихся не развертывающейся поверхности и т. д.
Двупараметрические семейства поверхностей имеют два свободных параметра. Например, множество сфер, проходящих через две фиксированные точки, или семейство сфер, касающихся плоскости и поверхности и т.д.

Рис. 14
В качестве примеров трехпараметрических множеств поверхностей можно привести:
- множество сфер, инцидентных фиксированной точке;
- множество сфер, касающихся плоскости и т. д.
Таким образом, все вышеизложенное, связанное с систематизацией проецирующих многообразий, можно представить в виде схемы (рис. 15). Заметим, что способов задания проецирующих множеств, отличающихся своими характеристиками бесконечное множество.

Рис. 15
Выбор тех или иных проецирующих множеств зависит от особенностей решаемых теоретических и прикладных задач. Кроме того, следует отметить, что в начертательной геометрии для моделирования применяется только связки линий, а остальные проецирующие многообразия ждут своих применений.
Систематизация носителей моделей
Носителями моделей, как раньше указывалось, в E3могут быть:
- кривая линия (прямая);
- поверхность (плоскость);
- трехмерное пространство.
Прямая как носитель модели применяется в аналитической геометрии, где оси координат являются носителями моделей, а проецирующим аппаратом являются плоскости, параллельные соответствующим координатным плоскостям (рис. 16).
Кривая линия как носитель модели применяется в дифференциальной геометрии (криволинейные координаты на поверхности). В начертательной геометрии прямая как носитель модели используется, например, в случае осевого проецирования.
Если за основной элемент пространства (оригинал) принять плоскость, то она в пересечении с фиксированной пространственной кривой линией  определяет систему точек. Полученная система точек на кривой линии а n определяет положение моделируемой плоскости в пространстве. При проецировании таких систем точек на плоскость
определяет систему точек. Полученная система точек на кривой линии а n определяет положение моделируемой плоскости в пространстве. При проецировании таких систем точек на плоскость  появляется возможность отобразить множество плоскостей пространства на систему точек, принадлежащих некоторой плоской кривой
появляется возможность отобразить множество плоскостей пространства на систему точек, принадлежащих некоторой плоской кривой  (рис.17).
(рис.17).

Рис. 16

Рис. 17
Плоскость как носитель модели широко используется в инженерной графике, например, в методе двух следов и двух изображений. Кроме плоскости в качестве носителей моделей применяются поверхности: полусфера, полуцилиндр, конус и другие алгебраические поверхности высших порядков. Интересное практическое применение полуцилиндрических и полусферических носителей моделей нашли при построении оптических изображений (кино, телевидение), в купольной и панорамной перспективе.
Рассмотрим примеры получения различных моделей одного и того же оригинала с различными аппаратами проецирования и на различных носителях моделей. В качестве оригинала возьмем точку пространства: в качестве аппарата проецирования связку прямых, точку будем проецировать на различные носители моделей и в качестве модели точки будем иметь:
- на плоскости – точку;
- на квадрике (поверхности второго порядка) – две точки;
- на торе – четыре точки;
аппарат проецирования – связка плоскостей:
- на плоскости – прямая;
- на квадрике – коника (кривая 2-го порядка);
- на торе – плоская кривая линия 4-го порядка;
аппарат проецирования – связка квадрик:
- на плоскости – коника;
- на квадрике – пространственная кривая линия 4-го порядка;
- на торе – пространственная кривая линия 8-го порядка и т.д.
В качестве оригинала возьмем в пространстве прямую, в качестве аппарата проецирования – связку прямых:
- на плоскости – пара точек;
- на квадрике – четыре точки;
- на торе – восемь точек;
в качестве аппарата проецирования – связка плоскостей:
- на плоскости – пара прямых;
- на квадрике – пара коник;
- на торе – пара плоских кривых 4-го порядка (потому, что прямая в пространстве определяется двумя точками, а две точки выделяют из связок аппаратов проецирования по два проецирующих элементов);
в качестве аппарата проецирования – связка квадратик:
- на плоскости – пара коник;
- на квадрике – пара пространственных кривых 4-го порядка;
- на торе – пара пространственных кривых 8-го порядка и т.д.
На приведенных примерах ярко видно влияние взаимного расположения аппарата проецирования и носителя модели на полученную модель. Если аппарат проецирования – связка квадрик, носитель модели – тор, то модель – пара пространственные кривые 8-го порядка которые могут распадаться на: пространственные кривые 6-го порядка и коники, на пространственные кривые 5-го порядка и на пространственные кривые 3-го порядка, на две пространственные кривые 4-го порядка, на четыре коники, которые могут совпадать. Если в качестве аппарата проецирования взять связку квадрик (линейчатых поверхностей) и носителем тоже линейчатую квадрику, то модель оригинала может распасться на несколько прямых и т. д.
Развитие начертательной геометрии тесно связано с научно-техническим прогрессом. До последнего времени изображение любого объекта выполнялось на плоскости, то есть трехмерный объект изображался на двухмерной плоскости. При современном развитии техники носителем моделей может быть и трехмерное пространство. Примером тому служит экран цветного телевизора, голографические и спектрографические изображения.
Применение различных носителей моделей вызвано необходимостью решения многочисленных сложных прикладных и теоретических задач.
Из приведенного выше анализа аппаратов проецирования и носителей моделей следует существование тесной взаимосвязи их характеристик. При этом различные модели оригиналов получаются всевозможными сочетаниями способов проецирования на различных носителях. Выше изложенная систематизация аппаратов проецирования и носителей моделей позволяет целенаправленно вести поиск необходимых аппаратов проецирования для получения изображений (моделей) пространственных форм, обладающих заданными свойствами.
Особо остро вопрос подбора аппарата проецирования встает при моделировании поверхностей в методе двух изображений, когда в качестве модели требуется получить взаимно однозначное соответствие.
I. 5. Моделирование основных геометрических форм в классических методах двух изображений и двух следов
Начертательная геометрия решает две задачи: прямую и обратную. При решении прямой задачи начертательной геометрии, т. е. моделировании, предметом изучения являются не реальные представители живой природы или объектов неорганического мира, а их условные модели – геометрические фигуры. Большинство геометрических фигур имеют три измерения. Для отображения трехмерных образов на плоскость необходимо иметь способы, позволяющие преобразовывать трехмерную фигуру (оригинал) в однозначно соответствующую ей модель, имеющую два измерения. В связи с этим возникает необходимость в создании науки, перебрасывающей мост между трехмерным пространством En и плоскостью чертежа E2. Наведение мостов между E3 и E2 осуществляется в начертательной геометрии с помощью метода проецирования, составляющего теоретическую основу начертательной геометрии. Как говорилось выше, в начертательной геометрии в качестве аппарата проецирования, в основном, используются связки прямых. Так, например, при моделировании точки на плоскости P через точку A (оригинал) проходит один луч связки (S) прямых, который отобразит точку A на плоскости P в точку ? (модель) (рис.18).

Рис. 18
При этом имеем, что одной точке пространства A ставится в соответствие одна точка А′ плоскости P, но обратное утверждение не имеет смысла, так как одной точке А′ плоскости P соответствует множество точек проецирующего луча SА′ Это несоответствие возникает из-за разности мерностей проецирующих множеств, так как множество точек A пространства E3 – ∞ 3, а множество точек А′ плоскости P – ∞2. Одна проекция точки на плоскости не только не позволяет определить положение ее оригинала, но и не позволяет судить по одной проекции о форме, размерах пространственных геометрических фигур.
Таким образом, возникает необходимость проецировать точку пространства из двух центров двумя связками прямых (S1) и (S2) для получения взаимно однозначного соответствия между оригиналом и моделью (рис.19).
На этом же рис. 19 покажем решение обратной задачи, т. е. по данной модели точки построить ее оригинал. Дана модель точки С - С1, С2 на прямой  пучка
пучка  прямых и аппарат проецирования – две связки S2 и S2 прямых, которые определяют прямую m. Прямые m ∩ c определяют плоскость Δ, в которой будем конструировать точку С для этого из пучка
прямых и аппарат проецирования – две связки S2 и S2 прямых, которые определяют прямую m. Прямые m ∩ c определяют плоскость Δ, в которой будем конструировать точку С для этого из пучка  прямых точка С1 выделит единственную прямую, а точка С2 из пучка
прямых точка С1 выделит единственную прямую, а точка С2 из пучка  прямых выделит единственную прямую, которые находясь в плоскости
прямых выделит единственную прямую, которые находясь в плоскости  , пересекутся в одной точке С. Так получается оригинал точки по ее модели.
, пересекутся в одной точке С. Так получается оригинал точки по ее модели.

Рис. 19
Признак обратимости чертежа (изображения): изображение (чертеж) являются обратимым, если равны мерности оригинала и изображения. Например, в методе двух изображений – основной элемент пространства – точка, моделируется на плоскости изображений парой точек, лежащих на линии связи. Так как точка A пространства из связки  прямых выделит единственную прямую, которая ее спроецирует на плоскость П в точку A1 на что будет затрачено ∞2. Точка A1 из пучка
прямых выделит единственную прямую, которая ее спроецирует на плоскость П в точку A1 на что будет затрачено ∞2. Точка A1 из пучка  прямых плоскости
прямых плоскости  единственную прямую
единственную прямую  . Точка A из связки
. Точка A из связки  прямых выделит единственную прямую, которая ее спроецирует на плоскость
прямых выделит единственную прямую, которая ее спроецирует на плоскость  в точку A2 на прямую
в точку A2 на прямую  на что будет затрачено
на что будет затрачено  . Точек в пространстве E3 – ∞ 3, точек на плоскости – ∞ 2, точек на луче А1A2 – ∞ 1, значит для определения пары точек на плоскости P потребуется затратить мерность ∞ 3, тогда мерность модели и оригинала будут равными. При моделировании точечных множеств возникают некоторые особенности, которые позволяют открывать особенности оригиналов по их моделям. Рассмотрим пример. Аппарат проецирования возьмем связки
. Точек в пространстве E3 – ∞ 3, точек на плоскости – ∞ 2, точек на луче А1A2 – ∞ 1, значит для определения пары точек на плоскости P потребуется затратить мерность ∞ 3, тогда мерность модели и оригинала будут равными. При моделировании точечных множеств возникают некоторые особенности, которые позволяют открывать особенности оригиналов по их моделям. Рассмотрим пример. Аппарат проецирования возьмем связки  и
и  прямых, которые определяют в пространстве прямую
прямых, которые определяют в пространстве прямую  , пересекающую плоскость
, пересекающую плоскость  в точке
в точке  и носитель модели плоскость
и носитель модели плоскость  . Точку C пространства проецируем из центров
. Точку C пространства проецируем из центров  и
и  в точки C1 и C2 на плоскость
в точки C1 и C2 на плоскость  (рис. 20).
(рис. 20).
Если в качестве оригинала будет выступать тело, то оно пучком m плоскостей будет расслаиваться на сечения, которые из центров (S1) и (S2) проецирования будут моделироваться в пучке  прямых на плоскости П.
прямых на плоскости П.
На оригинале точки могут быть: просто точка (как, например, точка С) двойная точка (как, например, точка  ), конкурирующие точки (как, например, точки
), конкурирующие точки (как, например, точки  и
и  ).
).

Рис. 20
Проекция точек А и В из центра проецирования  на носитель модели прямую
на носитель модели прямую  проецируются в конкурирующие точки
проецируются в конкурирующие точки  , которые образуют двойную точку, а из центра проецирования
, которые образуют двойную точку, а из центра проецирования  проецируются в пару точек
проецируются в пару точек  . Двойная точка
. Двойная точка  моделируется из центров проецирования
моделируется из центров проецирования  на носителе модели
на носителе модели  двойными точками
двойными точками  и
и  . Из вышеизложенного видим, что одна проекция точек не определяет их положение на оригинале. Если нам будут даны только проекции
. Из вышеизложенного видим, что одна проекция точек не определяет их положение на оригинале. Если нам будут даны только проекции  и
и  мы не сможем сделать заключение об оригиналах точек А, В и С, D, они могут быть на оригинале как двойная точка так и как конкурирующими.
мы не сможем сделать заключение об оригиналах точек А, В и С, D, они могут быть на оригинале как двойная точка так и как конкурирующими.
Геометрии бывают различные: аффинная геометрия, проективная геометрия, и т. д.
В аффинной геометрии прямая продолжается в разные стороны далеко, далеко, плоскость продолжается в любую сторону то же далеко, далеко. Аффинная плоскость двусторонняя и прямая на аффинной плоскости то же двусторонняя. На аффинной плоскости прямые пересекаются или не пересекаются, если они параллельные. Поэтому на аффинной плоскости не возможно взаимно однозначное соответствие, которое заключается в следующем: прямая на плоскости определяется двумя точками, но точка не определяется двумя прямыми, если они параллельные. Для устранения этого недостатка, договорились [6, 7, 8, 9 и др.], что параллельные прямые пересекаются в несобственной точке, введенной на аффинной плоскости и превратившей аффинную плоскость в проективную плоскость. На проективной плоскости возможно взаимно однозначное соответствие, т. к. прямая определяется двумя точками, а точка определяется в пересечении двух прямых. Введение несобственной точки на прямой оставило непонятным вопрос ее образования. Если рассматривать прямую на аффинной плоскости и ее организовать как числовую ось, т. е. на ней задать начало отсчета, масштаб и положительное направление, то двигаясь по ней вправо числа будут увеличиваться до  , при движении влево числа будут уменьшаться до
, при движении влево числа будут уменьшаться до  . Когда мы организуем проективную прямую, то прямая становить замкнутой. Если замыкание происходит точками
. Когда мы организуем проективную прямую, то прямая становить замкнутой. Если замыкание происходит точками  и
и  встык, то точки будут две, значит замыкание будет внахлест, т. е. точки
встык, то точки будут две, значит замыкание будет внахлест, т. е. точки  и
и  образуют двойную точку на модели и точки
образуют двойную точку на модели и точки  и
и могут быть только конкурирующими на оригинале. Проективная плоскость с точки зрения начертательной геометрии представляет одну проекцию ее оригинала и поэтому точки
могут быть только конкурирующими на оригинале. Проективная плоскость с точки зрения начертательной геометрии представляет одну проекцию ее оригинала и поэтому точки  и
и  на оригинале могут быть только конкурирующими. Оригинал проективной прямой можно представить как виток цилиндрической винтовой линии
на оригинале могут быть только конкурирующими. Оригинал проективной прямой можно представить как виток цилиндрической винтовой линии  [10, 11], (рис. 21) проекция которой на плоскость
[10, 11], (рис. 21) проекция которой на плоскость  является проективной прямой
является проективной прямой  .
.

Рис. 21
Все прямые проективной плоскости замыкаются на несобственной прямой, как «собачкой» на замке молнии замыкают проекцию проективную плоскость, делая ее односторонней. Оригинал проективной прямой – двусторонняя, оригинал проективной плоскости виток цилиндрической винтовой поверхности – двусторонняя.
Конкретизируем здесь вышеизложенное на примерах моделирования основных геометрических образов пространства E3 в методах двух изображения и двух следов. Аппарат метода двух изображений состоит, в общем случае, из плоскости P – основной плоскости проекций, двух вспомогательных плоскостей Π1 и Π2 и трех центров проецирования :S – основного, S1 и S2 – вспомогательных центров. Центры S, S1, S2 – коллинейны некоторой прямой m, пересекающей плоскость проекций P в исключенной точке F0. Произвольная точка A пространства изображается на плоскости P двумя точками A1 и A2 коллинейными с точкой F0. Сначала точка A проецируется из вспомогательных центров S1, S2 на вспомогательные плоскости Π1, Π2 соответственно в точки ?1, ?2, которые перепроецируются из основного центра S на плоскость P во вторичные проекции A1 и A2 (рис. 22).

Так как прямая  пространства определяется двумя ее точками A, B, то она на плоскости P будет изображаться двумя a1(A1, B1), a2(A2, B2) прямыми, соединяющими одноименные проекции точек. Плоскости в пространстве определяется тремя неколлинейными точками, например A, B, C (Σ (A, B, C)). Вторичные проекции Σ1 и Σ2 полей плоскости находятся в соответствии T11 гомологии, центром которой будет исключенная точка F0, осью гомологии будет двойная прямая d1= d2 полученная как проекция линии пересечения плоскости S с тождественной плоскостью F (ΣÇF = d). Прямая
пространства определяется двумя ее точками A, B, то она на плоскости P будет изображаться двумя a1(A1, B1), a2(A2, B2) прямыми, соединяющими одноименные проекции точек. Плоскости в пространстве определяется тремя неколлинейными точками, например A, B, C (Σ (A, B, C)). Вторичные проекции Σ1 и Σ2 полей плоскости находятся в соответствии T11 гомологии, центром которой будет исключенная точка F0, осью гомологии будет двойная прямая d1= d2 полученная как проекция линии пересечения плоскости S с тождественной плоскостью F (ΣÇF = d). Прямая  в пространстве определяет пучок плоскостей, среди которых есть плоскость, точки которой изображаются на плоскости изображения P совпавшими С1 = С2 вторичными проекциями. Такая плоскость F (S, l) называется тождественной. Множество всех плоскостей пространства будут моделироваться на плоскости изображения P гомологиями, имеющими общий центр точку F0, но различные оси гомологии. Из проективной геометрии [12] известно, между точками данной плоскости пространства и вспомогательными плоскостями Π1 и Π2 устанавливается перспективно коллинеарное соответствие. На плоскости проекций P имеем соответственные коллинеарные поля, в этом случае коллинеация называется гомологией, которая задается центром гомологии S (F0), осью гомологии
в пространстве определяет пучок плоскостей, среди которых есть плоскость, точки которой изображаются на плоскости изображения P совпавшими С1 = С2 вторичными проекциями. Такая плоскость F (S, l) называется тождественной. Множество всех плоскостей пространства будут моделироваться на плоскости изображения P гомологиями, имеющими общий центр точку F0, но различные оси гомологии. Из проективной геометрии [12] известно, между точками данной плоскости пространства и вспомогательными плоскостями Π1 и Π2 устанавливается перспективно коллинеарное соответствие. На плоскости проекций P имеем соответственные коллинеарные поля, в этом случае коллинеация называется гомологией, которая задается центром гомологии S (F0), осью гомологии  (d1=d2) и парой соответственных точек – (A1, A2). Гомологий на плоскости – ∞ 5, так как на гомологии – модели плоскостей пространства на плоскости проекций P не затрачиваются параметры на задание центра гомологии F0 , то таких гомологий на плоскости P будет ∞3.
(d1=d2) и парой соответственных точек – (A1, A2). Гомологий на плоскости – ∞ 5, так как на гомологии – модели плоскостей пространства на плоскости проекций P не затрачиваются параметры на задание центра гомологии F0 , то таких гомологий на плоскости P будет ∞3.
Частным случаем гомологии является элация – она получается на плоскости проекций P, когда m∩d и когда F0 ∈ d1=d2 (рис. 23, 24).

Рис. 23

Рис. 24
Если плоскость Σ пространства пересекает прямую m в точке K, которая образует гармоническую четверку (F0K S1S2) = -1, то гомология T11 – модель этой плоскости на P будет инволюционной ℑ1 (рис. 25).

Значит связка (K) плоскостей пространства будет моделироваться инволюционными гомологиями, которых на плоскости проекций P будет – ∞2, так как в этом случае не затрачивается параметр на задание соответственных точек гомологии, а их положение определяется из соотношения:
(F0 D A1 A2) = -1
или
(F0D) ~ (A1A2), где D = d1 = d2 ∩ (A1A2).
Пучок ( ) плоскостей моделируется на плоскости P гомологиями, имеющими общий центр F0 и общую ось гомологии исключенную прямую
) плоскостей моделируется на плоскости P гомологиями, имеющими общий центр F0 и общую ось гомологии исключенную прямую  , такие гомологии будут гиперболического типа и их на плоскости P будет ∞ 2 .
, такие гомологии будут гиперболического типа и их на плоскости P будет ∞ 2 .
Пучок (m) плоскостей моделируется на плоскости P пучком (F) двойных прямых, являющихся одновременно осями гомологий и носителями соответственных точек гомологий, такие гомологии будут гомологиями параболического типа и их на плоскости проекций P будет ∞1.
Если центр гомологии на плоскости будет несобственной точкой F0∞, тогда соответственные точки гомологии будут располагаться на параллельных прямых, такая гомология называется родством (рис. 26). Если центр и ось гомологии будут на плоскости несобственными элементами, то гомология будет перемещение (рис. 27).

Рис. 26

Рис. 27
Резюмируем выше изложенное:
в классическом методе двух изображений взаимно однозначными соответствиями на плоскости проекции моделируются оригиналы пространства:
- точка – парой точек;
- прямая – парой прямых;
- плоскость – гомологией.
В методе двух следов основным элементом является прямая. Аппарат классического метода двух следов состоит из плоскости изображения P, двух вспомогательных плоскостей Π1 и Π2 и центра проецирования S (рис. 28). Оригинал прямая  пересекает вспомогательные плоскости Π1 и Π2 в точках ?1 и ?2, которые из центра S проецируется на плоскость изображения P в точки A1 и A2, которые на плоскости P располагаются определенным образом относительно исключенной прямой
пересекает вспомогательные плоскости Π1 и Π2 в точках ?1 и ?2, которые из центра S проецируется на плоскость изображения P в точки A1 и A2, которые на плоскости P располагаются определенным образом относительно исключенной прямой  .
.

Плоскость Σ пространства E3 пересечет вспомогательные плоскости  и
и  по прямым
по прямым  и
и  , которые из центра S проецируются на плоскость P в пару прямых линий n1 и n2, пересекающих исключенную прямую
, которые из центра S проецируются на плоскость P в пару прямых линий n1 и n2, пересекающих исключенную прямую  . Точка P пространства определяется как центр связки прямых или как центр связки плоскостей, поэтому моделью точки в методе двух следов на плоскости изображений P будет гомология. Значит, в методе двух следов основные элементы пространства E3 будут моделироваться взаимно однозначными соответствиями:
. Точка P пространства определяется как центр связки прямых или как центр связки плоскостей, поэтому моделью точки в методе двух следов на плоскости изображений P будет гомология. Значит, в методе двух следов основные элементы пространства E3 будут моделироваться взаимно однозначными соответствиями:
- прямая – парой точек;
- плоскость – парой прямых;
- точка – гомологией.
Частными случаями аппаратов классических методов двух изображений и двух следов являются:
- эпюр Монжа,
- аксонометрия,
- перспектива,
- проекции с векторными отметками,
- проекции с числовыми отметками и. т.д.
Эпюр Монжа (комплексный чертеж) можно получить следующим образом.
Основную плоскость  совместить с вспомогательной плоскостью
совместить с вспомогательной плоскостью  , а плоскость
, а плоскость  расположить к ней перпендикулярно. За центр проецирования
расположить к ней перпендикулярно. За центр проецирования  принимаем бесконечно удаленную точку
принимаем бесконечно удаленную точку  , ортогонально – сопряженную с плоскостью
, ортогонально – сопряженную с плоскостью  , за центр
, за центр  ортогонально – сопряженную точку с плоскостью
ортогонально – сопряженную точку с плоскостью  . За центр
. За центр  принимается бесконечно удаленная точка ортогонально – сопряженная с биссекторной плоскость двугранного угла плоскостей
принимается бесконечно удаленная точка ортогонально – сопряженная с биссекторной плоскость двугранного угла плоскостей  и
и  , которая является тождественной плоскостью (рис. 29).
, которая является тождественной плоскостью (рис. 29).

Рис. 29
При таком выборе проецирующего аппарата вторичные проекции А2 точки А совпадут с ортогональной проекцией ?2 на плоскости изображения  . А вторичная проекция А1 может быть получена из ортогональной проекции ?1 путем совмещения поля
. А вторичная проекция А1 может быть получена из ортогональной проекции ?1 путем совмещения поля  с полем проекций
с полем проекций  вращением плоскости
вращением плоскости  вокруг линии пересечения плоскостей
вокруг линии пересечения плоскостей  и
и  . Исключенной точкой чертежа является бесконечно удаленная точка
. Исключенной точкой чертежа является бесконечно удаленная точка  , через которую проходят линии связи эпюра Монжа. Как видно из вышеизложенного, плоскость на эпюре Монжа будет моделироваться родством.
, через которую проходят линии связи эпюра Монжа. Как видно из вышеизложенного, плоскость на эпюре Монжа будет моделироваться родством.
В дальнейшем, не уменьшая общности рассуждений, будем предполагать, что вспомогательные плоскости проекций Π1 и Π2 совмещены с основной плоскостью проекций P. Основной центр проецирования помещен в точку S∞ в направлении, перпендикулярном плоскости P. В этом случае проекции точки A на вспомогательные плоскости совпадут с ее первичными проекциями на плоскости P, то есть ?1 =A1 , ?2 =A2.
I. 6. Конструирование кривых линий по их моделям
В связи с тем, что свойства поверхностей во многом определяются свойствами их линий, конструирование кривых представляет важную компоненту сложной задачи конструирования поверхностей, удовлетворяющих ряду наперед заданных условий. Существует непосредственная взаимосвязь свойств конструируемой кривой линии, свойств и положения порождающих ее проективных пучков линий. Последнее дает возможность прогнозировать свойства конструируемой кривой до ее непосредственного получения в виде одномерного массива точек.
Как было показано выше, в качестве носителей конструируемой кривой линии берется плоскость пучка  плоскостей, которая по i1 = i2 пересекает плоскость проекций П, а точка
плоскостей, которая по i1 = i2 пересекает плоскость проекций П, а точка  есть точка пересечения прямой
есть точка пересечения прямой  с плоскостью проекций П.
с плоскостью проекций П.
Таким образом, конструируемая кривая линия  порядка
порядка  является рациональной алгебраической кривой линией, имеющей одну
является рациональной алгебраической кривой линией, имеющей одну  – кратную точку
– кратную точку  и
и двойные точки, которые в зависимости от характеристик проецирующих пучков кривых могут быть собственными и несобственными, узловыми, изолированными и точками возврата.
двойные точки, которые в зависимости от характеристик проецирующих пучков кривых могут быть собственными и несобственными, узловыми, изолированными и точками возврата.
В инженерной практике применяются кривые высших порядков, имеющих наименьшее число действительных собственных кратных точек или без них. Рассмотрим на примере конструирования кривой линии четвертного порядка, как можно управлять типом ее двойных точек на стадии задания пучков коник, ее порождающих. Не распавшаяся кривая линия четвертого порядка может иметь три двойные или одну трехкратную точку, тогда она становится рациональной кривой линией. Количество и тип двойных точек конструируемой кривой линии определяется количеством и типом совпавших базисных точек проективных пучков кривых линий, порождающих конструируемую кривую линию:
1. При конструировании кривой линии  порядка p + q проективными пучками кривых линий cp, bq порядка p, q устанавливается взаимно однозначное соответствие между точками конструируемой кривой линией
порядка p + q проективными пучками кривых линий cp, bq порядка p, q устанавливается взаимно однозначное соответствие между точками конструируемой кривой линией  и прямолинейным носителей i1=i2 посредством проецирующих пучков кривых линий, что является признаком рациональности конструируемой кривой линии.
и прямолинейным носителей i1=i2 посредством проецирующих пучков кривых линий, что является признаком рациональности конструируемой кривой линии.
2. Конструируемая по описанной схеме кривая линия  имеет одну (p +q – 2) – кратную точку
имеет одну (p +q – 2) – кратную точку  и p +q – 2 двойных точек.
и p +q – 2 двойных точек.
При решении ряда инженерных задач, например, при обработке результатов эксперимента, в качестве аппроксимирующей или интерполирующей кривой линии используют моноидальные кривые линии имеющие точку максимальной кратности. Изложенный аппарат позволяет конструировать такие кривые линий. Для этого достаточно на прямолинейном носителе i1= i2 задать проективитет, у которого одна двойная точка совпадает с точкой  , которая будет вершиной (кратной точкой высшей кратности) для конструируемой кривой линии.
, которая будет вершиной (кратной точкой высшей кратности) для конструируемой кривой линии.
Таким образом, в заключение можно заметить, что рассмотренный нами аппарат конструирования кривых линий позволяет конструировать широкий класс рациональных кривых линий, имеющих ряд наперед заданных особенностей. Этот факт позволяет использовать предложенный аппарат для конструирования поверхностей, удовлетворяющих заданным требованиям позиционного характера, связанных с их инцидентностью дискретному каркасу кривых линий.
I. 7. Моделирование пространственных кривых линий
Рассмотрим центральное проецирование пространственных кривых линий на плоскость. Пространственная кривая линия  порядка n из точки
порядка n из точки  проецируется на плоскость P конусом Σ
проецируется на плоскость P конусом Σ (P,
(P,  ) порядка n с вершиной в точке P и направляющей кривой линией
) порядка n с вершиной в точке P и направляющей кривой линией  . Эта коническая поверхность Σ
. Эта коническая поверхность Σ (P,
(P,  ) пересекает плоскость P по кривой линии
) пересекает плоскость P по кривой линии  порядка n, если образующие конуса Σ
порядка n, если образующие конуса Σ являются его унисекантами. В этом случае касательная t в точке A кривой
являются его унисекантами. В этом случае касательная t в точке A кривой  проецируется в касательную t1 в точке A1 кривой линии
проецируется в касательную t1 в точке A1 кривой линии  (рис. 30).
(рис. 30).

Рис. 30
Если заставить приближаться точку P к A по прямой (PА), то проекция  в точке А1 будет уплощаться и при P=A проекция
в точке А1 будет уплощаться и при P=A проекция  распадается на прямую t1 и кривую
распадается на прямую t1 и кривую  порядка n-1. Здесь прямая t1 является следом соприкасающейся плоскости Г, построенная в точке Р=А к кривой
порядка n-1. Здесь прямая t1 является следом соприкасающейся плоскости Г, построенная в точке Р=А к кривой  . В том случае, когда пространственная кривая линия
. В том случае, когда пространственная кривая линия  имеет k – кратную точку B, проекция кривой линии
имеет k – кратную точку B, проекция кривой линии  из точки P=B распадается на k прямых и на кривую линию
из точки P=B распадается на k прямых и на кривую линию  порядка n – k .В этом случае прямые t k является следами соприкасающихся плоскостей, проходящих к k ветвям кривой линии
порядка n – k .В этом случае прямые t k является следами соприкасающихся плоскостей, проходящих к k ветвям кривой линии  в точке P=B.
в точке P=B.
Если каждая образующая конуса Σ (P,а n) пересекает направляющую кривую линию
(P,а n) пересекает направляющую кривую линию  в m точках, то проекция
в m точках, то проекция  на плоскости P будет порядка n/m -, потому, что в этом случае конус Σ
на плоскости P будет порядка n/m -, потому, что в этом случае конус Σ (Р, a ) распадается на m конусов , имеющих общую вершину Р и общие образующие.
(Р, a ) распадается на m конусов , имеющих общую вершину Р и общие образующие.
Таким образом, при проецировании пространственной кривой линии  на плоскость порядок проекции равен порядку оригинала лишь тогда, когда образующие конической поверхности являются ее унисекантами.
на плоскость порядок проекции равен порядку оригинала лишь тогда, когда образующие конической поверхности являются ее унисекантами.
Рассмотрим проецирование пространственной кривой линии  порядка r посредством конгруэнции Kr(n, k) прямых, заданной фокальными кривыми линиями
порядка r посредством конгруэнции Kr(n, k) прямых, заданной фокальными кривыми линиями  и
и  порядков
порядков  и
и
 соответственно, где
соответственно, где  . При произвольном расположении кривой линии
. При произвольном расположении кривой линии  относительно фокальных кривых линий
относительно фокальных кривых линий и
и  , аппарата отображения проекцией кривой линии
, аппарата отображения проекцией кривой линии  на плоскость П будет кривая линия
на плоскость П будет кривая линия  порядка
порядка  – след линейчатой поверхности Ф
– след линейчатой поверхности Ф о трех направляющих кривых линий
о трех направляющих кривых линий  , так как из теории конгруэнций известно, что порядок поверхности F равен произведению порядка погружаемой кривой линии
, так как из теории конгруэнций известно, что порядок поверхности F равен произведению порядка погружаемой кривой линии  на сумму порядка n и класса k данной конгруэнции.
на сумму порядка n и класса k данной конгруэнции.
Если пространственная кривая линия  пересекает фокальную кривую линию, например, кривую линию
пересекает фокальную кривую линию, например, кривую линию  в p простых точках Cp , то линейчатая поверхность о трех направляющих распадается на р конусов
в p простых точках Cp , то линейчатая поверхность о трех направляющих распадается на р конусов порядка
порядка  и на линейчатую поверхность
и на линейчатую поверхность 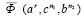 порядка r (n + k) – pn2 = 2rn2n1 – pn2.
порядка r (n + k) – pn2 = 2rn2n1 – pn2.
Если пространственная кривая линия  пересекает обе фокальные кривые линии, например,
пересекает обе фокальные кривые линии, например,  в р простых точках Ср кривую линию
в р простых точках Ср кривую линию  в q простых точках Bq , то линейчатая поверхность о трех направляющих распадается на p конусов
в q простых точках Bq , то линейчатая поверхность о трех направляющих распадается на p конусов 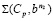 порядка
порядка  и на q конусов
и на q конусов 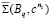 порядка
порядка  и на линейчатую поверхность
и на линейчатую поверхность 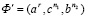 порядка r(n+k) – pn2 – qn1.
порядка r(n+k) – pn2 – qn1.
Если пространственная кривая линия ar пересекают фокальные кривые линии, например, кривую линию  в i – кратной точке C , а кривую линию
в i – кратной точке C , а кривую линию  в j – кратной точке B, то линейчатая поверхность о трех направляющих распадается на i конусов
в j – кратной точке B, то линейчатая поверхность о трех направляющих распадается на i конусов  порядка
порядка  и на j конусов
и на j конусов  порядка
порядка  и на линейчатую поверхность
и на линейчатую поверхность  порядка r (n + k) – in2 – jn1. Наивысшая кратность точек C и B может быть соответственно
порядка r (n + k) – in2 – jn1. Наивысшая кратность точек C и B может быть соответственно  и
и  в том случае, если фокальные кривые линии
в том случае, если фокальные кривые линии  ,
,  , будут плоскими кривыми линиями моноидального типа с вершинами в точках C и B соответственно.
, будут плоскими кривыми линиями моноидального типа с вершинами в точках C и B соответственно.
Таким образом, при проецировании пространственной кривой линии  на плоскость при помощи конгруэнций прямых Kг(n, k) в зависимости от положения погружаемой кривой линии
на плоскость при помощи конгруэнций прямых Kг(n, k) в зависимости от положения погружаемой кривой линии  относительно фокальных линий
относительно фокальных линий  ,
,  можно получить в качестве проекции данной кривой линии
можно получить в качестве проекции данной кривой линии  кривые линии, порядки которых изменяются в широком пределе. Существование этих пределов позволяет подбирать аппараты отображения пространственной кривой линии
кривые линии, порядки которых изменяются в широком пределе. Существование этих пределов позволяет подбирать аппараты отображения пространственной кривой линии  на плоскость с целью получения в качестве проекции кривой линии с наперед заданными характеристиками (порядка, числом и кратностью особых точек и т. д.).
на плоскость с целью получения в качестве проекции кривой линии с наперед заданными характеристиками (порядка, числом и кратностью особых точек и т. д.).
I. 8. Моделирование плоских кривых линий
Построение проекций кривых линий, расположенных в проецирующей плоскости, мы рассмотрим в контексте с основной задачей, связанной с изучением свойств поверхностей, несущих в пучке  плоскостей каркас кривых линий аiv порядка v=2. Плоскости
плоскостей каркас кривых линий аiv порядка v=2. Плоскости  пересекаясь с плоскостью изображения П, образуют носители
пересекаясь с плоскостью изображения П, образуют носители  , на которых устанавливается соответствия, получаемые при двойном проецировании линий
, на которых устанавливается соответствия, получаемые при двойном проецировании линий  каркаса поверхности определенным аппаратом.
каркаса поверхности определенным аппаратом.
I. 8. 1. Моделирование плоских кривых линий двумя пучками прямых
Рассмотрим случай моделирования кривых линий второго порядка проецированием двумя пучками прямых (S1), (S2), расположенных в плоскости кривой линии.
При произвольном расположении центров проецирования S1, S2 относительно модулируемой кривой линии  на носителе i1 = i2 устанавливается (2÷2) – значное соответствие, так как одной точке ?1 , носителя i1 соответствуют две точки, которые из второго центра S2 проецируются на носитель i2 в две точки ?2, B2 (рис. 31).
на носителе i1 = i2 устанавливается (2÷2) – значное соответствие, так как одной точке ?1 , носителя i1 соответствуют две точки, которые из второго центра S2 проецируются на носитель i2 в две точки ?2, B2 (рис. 31).

Рис. 31
Аналогично одной точке A2 ряда i2 соответствует две точки ?1, B1 ряда i1. Чтоб получить взаимно однозначное соответствие при проецировании коники двумя пучками прямых, центры проецирования необходимо поместить на конику. Тогда каждая проецирующая прямая пучка прямых пересечет конику и носитель  (рис. 32).
(рис. 32).

Рис. 32
Таким образом, в этом случае моделью коники  на прямолинейном носителе
на прямолинейном носителе  будет взаимно однозначное (проективное) соответствие. Точки пересечения коники
будет взаимно однозначное (проективное) соответствие. Точки пересечения коники  с носителем
с носителем  являются двойными точками проективитета (модели). Проективные соответствия в зависимости от количества и типа двойных точек могут быть гиперболическими (двойные точки различные и действительные) (рис. 33, а), параболическими (действительные точки совпадают) (рис. 33, б), эллиптическими (две различные мнимые точки) (рис. 33, в), не инволюционными (рис.33, г), инволюционными (рис. 33, д). При совпадении одной двойной точки с несобственной точкой носителя
являются двойными точками проективитета (модели). Проективные соответствия в зависимости от количества и типа двойных точек могут быть гиперболическими (двойные точки различные и действительные) (рис. 33, а), параболическими (действительные точки совпадают) (рис. 33, б), эллиптическими (две различные мнимые точки) (рис. 33, в), не инволюционными (рис.33, г), инволюционными (рис. 33, д). При совпадении одной двойной точки с несобственной точкой носителя  проективитет вырождается в аффинитет (рис. 33, е).
проективитет вырождается в аффинитет (рис. 33, е).
Далее рассмотрим моделирование плоских кривых линий третьего порядка  , которые могут быть жанра 1 и 0 (жанр (род) алгебраической кривой линии равен разности между наибольшим числом двойных точек кривой и фактическим числом двойных точек) (рис. 34 а, б).
, которые могут быть жанра 1 и 0 (жанр (род) алгебраической кривой линии равен разности между наибольшим числом двойных точек кривой и фактическим числом двойных точек) (рис. 34 а, б).

Рис. 33

Рис. 34
На рис. 34,б изображена кривая линия  жанра 0. В зависимости от расположения центров проецирования относительно моделируемой кривой
жанра 0. В зависимости от расположения центров проецирования относительно моделируемой кривой  можно получить следующие виды соотношений на i1 = i2:
можно получить следующие виды соотношений на i1 = i2:
а) если центры проецирования не инцидентны кривой линии  , то моделью кривой линии на носители i1 = i2 будет (3 ÷3) – значное соответствие;
, то моделью кривой линии на носители i1 = i2 будет (3 ÷3) – значное соответствие;
б) если один центр проецирования не инцидентен кривой линии  , а другой центр проецирования инцидентен простой точке кривой линии
, а другой центр проецирования инцидентен простой точке кривой линии  , то моделью кривой линии
, то моделью кривой линии  на носители i1= i2 будет (3 ¸ 2) – значное соответствие;
на носители i1= i2 будет (3 ¸ 2) – значное соответствие;
в) если центры проецирования инцидентны простым точкам кривой линии  , то на носителе i1 = i2 будет моделироваться (2¸ 2) – соответствие;
, то на носителе i1 = i2 будет моделироваться (2¸ 2) – соответствие;
г) если один центр проецирования инцидентен простой точке кривой линии  , а второй центр проецирования инцидентен двойной точке кривой линии
, а второй центр проецирования инцидентен двойной точке кривой линии  жанра 0, то на носителе i1 = i2 будет моделироваться (2¸1) – значное соответствие.
жанра 0, то на носителе i1 = i2 будет моделироваться (2¸1) – значное соответствие.
Таким образом, из вышеизложенного видно, что при использовании двух центральных проецирований кривую линии  порядка 3 невозможно моделировать на прямолинейном носителе i1 = i2 взаимно однозначным соответствием. Аналогично можно показать, что в случае проецирования плоских кривых линий порядка n>2 двойным центральным проецированием на прямолинейный носитель i1 = i2 невозможно получить взаимно однозначное соответствие.
порядка 3 невозможно моделировать на прямолинейном носителе i1 = i2 взаимно однозначным соответствием. Аналогично можно показать, что в случае проецирования плоских кривых линий порядка n>2 двойным центральным проецированием на прямолинейный носитель i1 = i2 невозможно получить взаимно однозначное соответствие.
I. 8. 2. Криволинейное проецирование плоских кривых линий
Рассмотрим моделирование плоской кривой линии  порядка 3 жанра 0 проецированием пучком прямых (S) и пучком коник, которые заданны четырьмя базисными точками 1,2,3,4 на прямолинейном носителе i1 = i2 . (Коника – кривая линия второго порядка на плоскости определяется пятью параметрами или, например, пятью точками. Если закрепить четыре параметра или четыре точки, то получим пучок коник на плоскости).
порядка 3 жанра 0 проецированием пучком прямых (S) и пучком коник, которые заданны четырьмя базисными точками 1,2,3,4 на прямолинейном носителе i1 = i2 . (Коника – кривая линия второго порядка на плоскости определяется пятью параметрами или, например, пятью точками. Если закрепить четыре параметра или четыре точки, то получим пучок коник на плоскости).
Проецирование при помощи кривых линий называется криволинейным проецированием. При произвольном положении базисных точек пучков относительно друг друга, моделируемой кривой линии и прямолинейного носителя i1 = i2 можно получить в качестве моделей соответствия различной значимости. Если базисные точки пучков прямых и коник не инцидентны кривой  , на прямолинейном носители моделируется (6¸6) – значное соответствие. Значность соответствие, получаемого на прямолинейном носителе снизится до (2¸2) – значного, если базисные точки пучков проецирующих линий будут инцидентны простым точкам кривой линии
, на прямолинейном носители моделируется (6¸6) – значное соответствие. Значность соответствие, получаемого на прямолинейном носителе снизится до (2¸2) – значного, если базисные точки пучков проецирующих линий будут инцидентны простым точкам кривой линии  .
.
Рассмотрим ограничения, которые необходимо наложить на взаимное положение базисных точек пучков проецирующих кривых линии, носителя i1 =i2 и кривой линии  для получения взаимно однозначного соответствия.
для получения взаимно однозначного соответствия.
1. При проецировании пучком коник каждая коника  (рис. 35) пучка (1234) коник должна пересекать прямолинейный носитель i1 = i2 в одной свободной точке,
(рис. 35) пучка (1234) коник должна пересекать прямолинейный носитель i1 = i2 в одной свободной точке,  например А2, что обеспечивается инциденцией прямолинейного носителя одной базисной точки пучка коник, например, точке 4.
например А2, что обеспечивается инциденцией прямолинейного носителя одной базисной точки пучка коник, например, точке 4.
2. При проецировании пучком  прямых, каждая прямая пучка
прямых, каждая прямая пучка  должна пересекать прямолинейный носитель i1 = i2 в одной свободной точке, например
должна пересекать прямолинейный носитель i1 = i2 в одной свободной точке, например  , и кривую линию
, и кривую линию  в одной свободной точке, например А, поэтому точку S помещаем в двойную точку P кривой линии
в одной свободной точке, например А, поэтому точку S помещаем в двойную точку P кривой линии  ,т.е. S=P.
,т.е. S=P.
3. Каждая коник  пучка (1 2 3 4) коник должна пересекать линию
пучка (1 2 3 4) коник должна пересекать линию  в одной свободной точке, например А, а кривая линия
в одной свободной точке, например А, а кривая линия  с коникой пересекается в 6-ти точках, значит для обеспечения одного свободного их пересечения, необходимо 5 точек их взаимного пересечения зафиксировать, что возможно, если базисные точки 1,2,3,4 пучка (1234) коник будут инцидентны линии
с коникой пересекается в 6-ти точках, значит для обеспечения одного свободного их пересечения, необходимо 5 точек их взаимного пересечения зафиксировать, что возможно, если базисные точки 1,2,3,4 пучка (1234) коник будут инцидентны линии  , при чем одна из базисных точек пучка (1 2 3 4), например, 1 будет совпадать с двойной точкой оригинала P, т. е. S=1=P.
, при чем одна из базисных точек пучка (1 2 3 4), например, 1 будет совпадать с двойной точкой оригинала P, т. е. S=1=P.

Рис. 35
Только в этом случае кривая линия  будет моделироваться на i1= i2 (1÷1) – значным соответствием. Действительно, точка
будет моделироваться на i1= i2 (1÷1) – значным соответствием. Действительно, точка  выделяет из пучка (S) прямых единственную прямую, например,
выделяет из пучка (S) прямых единственную прямую, например,  , которая пересекает линию
, которая пересекает линию  и носитель i1= i2 каждую в одной точке A и A1 . Точка
и носитель i1= i2 каждую в одной точке A и A1 . Точка  выделяет из пучка, (1 2 3 4) коник единственную конику, например,
выделяет из пучка, (1 2 3 4) коник единственную конику, например,  , которая пересекает линию
, которая пересекает линию  и носитель i1= i2 каждую в одной точке A, A2. Значит, точка A моделируется на прямолинейном носителе i1= i2 парой соответственных точек A1 ~ A2.
и носитель i1= i2 каждую в одной точке A, A2. Значит, точка A моделируется на прямолинейном носителе i1= i2 парой соответственных точек A1 ~ A2.
В общем случае при моделировании алгебраической кривой линии  порядка
порядка  на прямолинейном носителе i1= i2 двумя пучками кривых линий
на прямолинейном носителе i1= i2 двумя пучками кривых линий  порядков
порядков  и
и  для получения (1÷1) – значного соответствия необходимо выполнение следующих условий.
для получения (1÷1) – значного соответствия необходимо выполнение следующих условий.
1. Каждая кривая линия  данных пучков кривых линий прямолинейный носитель i1= i2 должны пересекать в одной свободной точке, что можно достичь двумя путями:
данных пучков кривых линий прямолинейный носитель i1= i2 должны пересекать в одной свободной точке, что можно достичь двумя путями:
а) Инциденцией определенного количества базисных точек пучков кривых линий прямолинейному носителю i1= i2;
б) Выбора в качестве кривых линий  пучков кривых линий, кривые линии моноидального типа с общей вершиной, например, точкой F0 , инцидентной прямолинейному носителю i1= i2.
пучков кривых линий, кривые линии моноидального типа с общей вершиной, например, точкой F0 , инцидентной прямолинейному носителю i1= i2.
2. Пучки проецирующих кривых линий  соответственно порядков
соответственно порядков  и
и  должны иметь
должны иметь  общих базисных точек.
общих базисных точек.
Действительно, чтобы точка  моделировалась парой соответственных точек A1 ~ A2 на прямолинейном носителе i1= i2, проецирующие кривые линии
моделировалась парой соответственных точек A1 ~ A2 на прямолинейном носителе i1= i2, проецирующие кривые линии  порядков
порядков  и
и  должны пересекаться в одной свободной точке A, остальные точки их пересечения должны быть фиксированными. Кривые линии
должны пересекаться в одной свободной точке A, остальные точки их пересечения должны быть фиксированными. Кривые линии  пересекаются в
пересекаются в  точках, из которых (v – k – 1)(k – 1) приходятся на вершину F0, так как она
точках, из которых (v – k – 1)(k – 1) приходятся на вершину F0, так как она  - и
- и - кратна на прямолинейном носителе i1= i2.
- кратна на прямолинейном носителе i1= i2.
Поэтому проецирующие кривые линии  кроме точек F0 и A будут иметь еще (v – k)k(v – k – 1)(k – 1) – 1 = v – 2 общих точек Qi.
кроме точек F0 и A будут иметь еще (v – k)k(v – k – 1)(k – 1) – 1 = v – 2 общих точек Qi.
3. Из проективного способа образования кривых следует, что общие базисные точки проективных пучков кривых линий являются двойными для порождаемой кривой, в нашем случае для кривой линии  , поэтому кривая линия
, поэтому кривая линия  должна иметь
должна иметь  двойных точек Qi. Кроме того, кривая линия
двойных точек Qi. Кроме того, кривая линия  пересекает носитель i1= i2. в двух двойных точках проективитета, поэтому точка F0 принадлежит кривой линии
пересекает носитель i1= i2. в двух двойных точках проективитета, поэтому точка F0 принадлежит кривой линии  и является для нее (
и является для нее ( ) – кратной точкой.
) – кратной точкой.
4. Каждая кривая линия  пучка кривых линий должна пересекаться с моделью лишь в одной свободной точке A. Поэтому пучок кривых линий (ck) должен иметь н модели кривой линии
пучка кривых линий должна пересекаться с моделью лишь в одной свободной точке A. Поэтому пучок кривых линий (ck) должен иметь н модели кривой линии  кроме
кроме  - кратной базисной точки F0 и v – 2 базисных точки Qi еще
- кратной базисной точки F0 и v – 2 базисных точки Qi еще
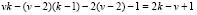
базисных точек. А пучок кривых линий  должен иметь еще
должен иметь еще
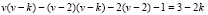
базисных точки.
Из теории известно, что ( ) – кратная точка кривой линии
) – кратная точка кривой линии  эквивалентна (
эквивалентна ( )(
)( )/2 двойным точкам. Значит кратные точки кривой линии
)/2 двойным точкам. Значит кратные точки кривой линии  эквивалентны
эквивалентны
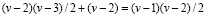
двойным точкам, то есть максимально возможному числу двойных точек. Поэтому оригинал  должен быть рациональной алгебраической кривой линией (жанра 0). Значит, справедливо предложение: плоская рациональная алгебраическая кривая линия
должен быть рациональной алгебраической кривой линией (жанра 0). Значит, справедливо предложение: плоская рациональная алгебраическая кривая линия  с (
с ( ) – кратной точкой
) – кратной точкой  и (
и ( ) двойными точками Qi моделируется на прямолинейном носителе i1= i2 взаимно однозначным соответствием. При проецировании двумя пучками моноидальных кривых линий
) двойными точками Qi моделируется на прямолинейном носителе i1= i2 взаимно однозначным соответствием. При проецировании двумя пучками моноидальных кривых линий  , имеющих общую вершину F0 и общие
, имеющих общую вершину F0 и общие  базисные точки Qi, если первый пучок кривых линий имеет на кривой линией
базисные точки Qi, если первый пучок кривых линий имеет на кривой линией  дополнительно
дополнительно  базисных точки, а второй пучок –
базисных точки, а второй пучок –  базисных точки.
базисных точки.
Таким образом, используя криволинейное проецирование значительно расширяется круг плоских кривых линий, которые могут отображаться на прямолинейный носитель взаимно однозначными соответствиями.
Библиографическая ссылка
Вертинская Н.Д. РЕШЕНИЯ ЗАДАЧ В МЕТОДАХ МОДЕЛИРОВАНИЯ И КОНСТРУИРОВАНИЯ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ // Научное обозрение. Технические науки. 2016. № 3. С. 5-25;URL: https://science-engineering.ru/ru/article/view?id=1084 (дата обращения: 04.03.2026).


 science-review.ru
science-review.ru