science-review.ru
Введение
Пластинки, как элементы несущих и ограждающих конструкций, широко распространены в строительстве и специальном машиностроении (судо- и авиастроении). Одной из важнейших задач при расчете пластинок является оценка их жесткости. Точные методы определения прогибов пластинок известны лишь для некоторых форм пластинок при простых видах граничных условий и нагрузки [1, 104]. Как правило, это прямоугольные и круглые пластинки при однородных граничных условиях. На практике часто встречаются пластинки сложной формы и сложными граничными условиями.
Такие задачи решаются с привлечением различных приближенных методов, чаще всего численных, реализуемых в современных программных комплексах: SCAD, ANSYS и др. Однако эти методы обладают известным существенным недостатком, заключающемся в выполнении однократного расчета и отсутствии возможности качественной и количественной оценки полученного результата среди всего множества форм пластинок с выпуклым контуром и идентичными граничными условиями.
Этого недостатка лишены геометрические методы строительной механики, основанные на физико-геометрической аналогии интегральных физико-механических характеристик (ФМХ) пластинок и интегральной геометрической характеристикой – коэффициентом формы Кf односвязной области с выпуклым контуром (термин «коэффициент формы» введен в строительную механику В.И. Коробко).
Такие методы широко используются при решении двумерных задач математической физике [103], когда для оценки интегральной ФМХ заданной области строятся одно- или двусторонние изопериметрические неравенства, основанные на изопериметрических свойствах коэффициента формы.
К решению некоторых двумерных задач строительной механики пластинок изопериметрический метод (ИЗПМ) впервые применил В.И. Коробко. В 1975 году он использовал его при решении задачи о несущей способности пластинок, находящихся в предельном состоянии [50]. Именно с этой статьи началось активное развитие изопериметрического метода. Благодаря исследованиям В.И. Коробко и работам его многочисленных учеников этот метод получил существенное развитие по многим направлениям.
В настоящее время из него выделились два новых инженерных метода, позволяющих определять интегральные ФМХ уже не с помощью неравенств, а с помощью аналитических зависимостей, которые строятся для определенного подмножества областей. В этих аналитических зависимостях геометрическими аргументами являются коэффициент формы и отношение внутреннего к внешнему конформных радиусов ?/?r . Поэтому первый из указанных методов назвали методом интерполяции по коэффициенту формы (МИКФ), а второй – методом интерполяции по отношению конформных радиусов (МИОКР).
К числу задач, которые могут быть исследованы этими методами, относятся поперечный изгиб, свободные колебания и устойчивость упругих пластинок, а также чистое кручение упругого стержня. При этом находятся: величина максимального прогиба пластинок w0, основная частота колебаний их в ненагруженном состоянии w, критическое усилие при равномерном всестороннем сжатии пластинок q0, геометрическая жесткость сечения G.
В настоящей обзорной статье показаны основные этапы работ по разработке, развитию и совершенствованию указанных геометрических методов за последние 30 лет.
1. Коэффициент формы односвязной области с выпуклым контуром
Коэффициент формы односвязной области с выпуклым контуром определяется с помощью контурного интеграла
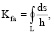(1)
где ds – элементарный участок контура некоторой двумерной области,
h – перпендикуляр, опущенный из произвольной точки «а», называемой полюсом, на участок контура ds (рис. 1).
Из выражения (1) для областей с криволинейным контуром (рис. 1,а) получим:
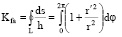, (2)
где r = r(φ) – полярное уравнение контура области с полюсом в точке «а», а для областей с полигональным контуром (рис. 1,б):
а) б)
Рис. 1. К определению коэффициента формы а) область с криволинейным контуром; б) область с полигональным контуром
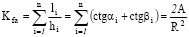,(3)
где n – количество сторон многоугольника;
А – площадь области;
R – максимальный радиус вписанной окружности; остальные обозначения указаны на рисунке.
Как показано в многочисленных работах по рассматриваемой проблеме, эта характеристика является геометрическим аналогом интегральных физических характеристик в двумерных задачах строительной механики, теории упругости и пластичности и широко используется при решении двумерных задач математической физики [103] и теории упругости [18]. В связи с этим многие сложные двумерные задачи теории упругости сводятся к решению элементарной геометрической задачи – анализу изменения свойств коэффициента формы при различных геометрических преобразованиях заданной области.
В любой выпуклой области (рисунок 1) существует единственная точка «a», для которой значение коэффициента формы минимально [103]: min Kfa = Kf. Именно эти значения коэффициента формы используются далее в рассматриваемом методе. В работах [18, 83] приведены формулы для определения Kf выпуклых областей различного очертания и подробные исследования его изопериметрических свойств.
Коэффициент формы обладает целым рядом «замечательных» изопериметрических свойств и закономерностей, которые и составили теоретическую основу геометрических методов.
Укажем наиболее значимые из них.
1. Kf дает количественную оценку формы геометрических фигур с выпуклым контуром и может служить критерием для оценки их «правильности» (симметричности): чем меньше Kf, тем более «правильнее» фигура.
2. Из всего множества выпуклых фигур наименьшее значение Kf = 2p имеет круг; из всех четырёхугольников наименьшее значение Kf = 8 имеет квадрат; из всех треугольников наименьшее значение Kf = 10,392 имеет равносторонний треугольник.
3. Всё множество коэффициентов формы для фигур с выпуклым контуром, представленное в виде функции параметра R/r, ограничено сверху значениями Kf для многоугольников, все стороны которых касаются вписанной окружности (в том числе правильных n-угольников и равнобедренных треугольников), а снизу – значениями Kf для эллипсов Здесь r – минимум радиусов кругов, описанных вокруг области.
4. Всё множество коэффициентов формы четырёхугольных выпуклых фигур, представленные в координатах Kf – R/ρ, ограничены сверху значениями Kf для треугольников и многоугольников, все стороны которых касаются вписанной окружности, а снизу – значениями Kf для прямоугольников.
5. Всё множество значений Kf для параллелограммов равной высоты, представленное в координатных осях Kf – R/r, ограничено сверху значениями Kf для ромбов, снизу – для прямоугольников: всё множество значений Kf для трапеций, представленное в координатах Kf – R/ρ, ограничено сверху значениями коэффициентов формы для треугольников и многоугольников, все стороны которых касаются вписанной окружности, снизу – для прямоугольников.
Все указанные выше свойства коэффициента формы представлены графически на рисунке 2.
Рис. 2. Графическое представление свойств коэффициента формы
I – правильные многоугольники; II – равнобедренные треугольники; III – эллипсы; IV – прямоугольники; V – ромбы; VI – аффинно-правильные шестиугольники; r – минимальный радиус описанной окружности
В математической физике известна другая интегральная физическая характеристика формы односвязной области с выпуклым контуром – отношение конформных радиусов – внутреннего к внешнему 
. Это отношение было впервые использовано в качестве обобщенного геометрического аргумента в работах В.И. Коробко и А.Н. Хусточкина для решения задач устойчивости пластинок [72, 73, 74, 76, 79].
Формулы для нахождения внутреннего 
и внешнего 
конформных радиусов для целого ряда односвязных областей с выпуклым контуром известны из теории конформных отображений [2, 3, 103]:
– для круга радиуса a
(3)
– для правильных n-угольников
;
, (4)
где n – число сторон;
L – периметр;
Г(x) – Гамма-функция;
– для произвольных треугольников с углами 
, 
, (5)
где 
;
r – радиус описанного круга;
– для ромбов с углом πα
,
, (6)
где α – угол ромба;
– для эллипсов с полуосями a и b (a ≥ b)
,
, (7)
где 
– для прямоугольников со сторонами a и b (a ≥ b)
, (8)
где 
α – аргумент комплексных чисел – точек окружности, образами которых при конформном отображении служат вершины прямоугольника, при этом, центр прямоугольника совпадает с началом координат, а стороны параллельны координатным осям; принято (-1)!! = 1.
Сопоставление изопериметрических свойств коэффициента формы и отношения конформных радиусов [86, 92, 93, 94, 114] показало их полную идентичность. В связи с этим методики применения МИКФ и МИОКР оказались практически одинаковыми.
3. Изопериметрический метод (ИЗПМ)
Теоретические основы изопериметрического метода для решения задач строительной механики пластинок разработаны профессором В.И. Коробко и представлены в его публикациях [50, …, 72]. В основу этого метода положены:
– свойство о двусторонней ограниченности коэффициента формы для всего множества областей с выпуклым контуром (рис. 2);
– свойства геометрической операции симметризации Штейнера при преобразовании таких областей.
Рис. 3. Границы изменения интегральных физических характеристик F
При исследовании интегро-дифференциальных соотношений двумерных задач теории упругости и строительной механики удалось выделить из них в явном виде коэффициент формы области [54, 55, 57, 64]. А поскольку интегральные физические характеристики (F) в рассматриваемых задачах функционально зависят от свойств коэффициента формы, то графическое представление зависимости F(Кf) убедительно показало, что все множество значений F обладают точно такими же изопериметрическими свойствами, что и коэффициент формы.
По аналогии с рисунком 2 на рисунке 3 построены зависимости F(1/Кf), где граничные кривые соответствуют тем же кривым, что и на рисунке 2. Аргумент 1/Кf принят для удобства графического представления рассматриваемых графиков.
Из рисунка 3 вытекает сущность изопериметрического метода. Путем использования, например, точных и приближенных численных методов необходимо построить граничные кривые, указанные на рисунке 3. Для получения двусторонних изопериметрических неравенств для оценки интегральной величины F заданной области (пластинки, мембраны, сечения) определяется коэффициент формы, строится вертикаль, соответствующая этому Кf, точки пересечения этой вертикали с граничными кривыми дают границы изменения искомой величины F.
Другой способ реализации изопериметрического метода заключается в следующем. Пусть, например, задана трапецеидальная шарнирно опертая по контуру пластинка, нагруженная равномерно распределенной нагрузкой. Путем симметризации этой пластинки или с использованием аффинных преобразований преобразуем ее в треугольную и прямоугольную пластики (т. 3 и т. 5 на рисунке 3). Значения максимального прогиба для этих пластинок дают двусторонние границы искомого решения для заданной трапецеидальной пластинки.
Первыми работами по развитию ИЗПМ были публикации [50, 51, 59]. Обобщающие результаты этих работ приведены в монографии [60]. Функциональная связь F и Kf в задачах технической теории пластинок была установлена в работах [52, 54, 55]. В статье [53] ИЗПМ использовался для решения задач поперечного изгиба пластинок, в статье [56] – задач устойчивости пластинок, а в статье [58] – задач свободных колебаний пластинок. В статьях [61, 62, 63, 65] была подробно исследована геометрическая сторона задачи: геометрические преобразования, графическое представление границ, графоаналитический способ определения интегральных ФМХ. В статье [66] ИЗПМ был применен к решению задачи чистого кручения призматического бруса.
В статьях [67, 68] рассматривались вопросы сравнимости F и Кf в задачах строительной механики, описываемых уравнениями эллиптического типа второго и четвертого порядка, а в статьях [71, 75] исследовалась возможность использования ИЗПМ в задачах расчета пластинок на упругом основании.
В монографиях [77, 80] подытожены результаты исследований по развитию и применению ИЗПМ к решению двумерных задач строительной механики и теории упругости. В статье [78] отмечены недостатки ИЗПМ, изложены перспективы его развития. Среди одного из указанных направлений предлагается разработать метод расчета, который бы позволял получать аналитические решения, связывающие функционально интегральные ФМХ с коэффициентом формы области. Эту статью можно считать отправной точкой, от которой началась разработка и развитие нового инженерного метода решения двумерных задач строительной механики, который в дальнейшем получил название метод интерполяции по коэффициенту формы.
4. Метод интерполяции по коэффициенту формы
На начальном этапе разработки и развития метода интерполяции по коэффициенту форм использовался прием непрерывного геометрического преобразования заданной области, при котором получаются такие области, решения для которых известны, причем искомое решение находится между решениями для этих двух областей. При этом все промежуточные фигуры объединены каким-либо одним геометрическим параметром: отношение сторон, угол при вершине треугольника, угол между сторонами ромба, угол для секториальных областей и т.п. Используя этот параметр как аргумент в некоторой функции, приводящей к удовлетворению «граничным» решениям, получают приближенную аналитическую зависимость, объединяющую все решения для полученного подмножества областей при выбранном геометрическом преобразовании. Для нахождения интегральной ФМХ для заданной области необходимо в полученную аналитическую зависимость подставить аргумент, соответствующий заданной области (рисунок 3, точка а на кривой 3-5). Именно так были получены решения в статьях [4, …, 12] при исследовании задач чистого кручения секториальных и параллелограммных сечений, а также в задачах поперечного изгиба параллелграммных и трапецеидальных пластинок. В статье [12] предлагаемый метод поучил свое название как метода интерполяции по коэффициенту формы, поскольку в ней было предложено для любых областей с выпуклым контуром при подборе аналитических зависимостей для определенного подмножества областей, объединенных одним геометрическим преобразованием, использовать коэффициент формы. В статье [13] был реализован такой подход для параллелограммных пластинок, а в статьях [15, 17] были изложены общие принципы решения задач строительной механики с помощью МИКФ.
В связи с тем, что коэффициент формы стал использоваться как основной геометрический аргумент в МИКФ, возникла потребность в более тщательном изучении его изопериметрических свойств и закономерностей. Этим вопросам были посвящены статьи [14, 16, 21, 24, 29], а также обобщающие работы [18, 83].
Помимо используемого приема геометрических преобразований с помощью симметризации Штейнера при практической реализации МИКФ к решению многих задач начали широко применяться аффинные преобразования [20].
В статье [19] был показан путь дальнейшего развития МИКФ в задачах поперечного изгиба пластинок для построения полей перемещений и внутренних усилий. Это направление исследований пока остается без внимания современных ученых.
Для облегчения нахождения граничных решений было предложено построить функциональные зависимости F(Kf), решив все рассматриваемые задачи для множества областей, образующих границы, с помощью численных методов с использованием МКЭ. Эта достаточно большая и трудоемкая работа была выполнена силам молодых исследователей, причем для четырехугольных и треугольных пластинок были рассмотрены все возможные комбинации граничных условий, включая шарнирное опирание и жесткую заделку по сторонам. Наличие граничных кривых позволяет разработать программные комплексы для решения рассматриваемых задач с графическим представлением результатов [28, 44, 45, 48]. Эти работы в настоящее время ведутся творческим коллективом Приокского государственного университета.
Все последующие работы связаны с разработкой и применением МИКФ к решению различных двумерных задач строительной механики. В работе [22] рассмотрена физическая аналогия в задачах кручения призматических брусьев и колебаний мембран. При этом было установлено, что по частоте колебаний мембран можно определить геометрическую жесткость кручения бруса и, наоборот, по жесткости кручения определить основную частоту колебаний мембран (формы сечения и мембран подобны). В статье [23] была исследована изопериметрическая проблема при кручении тонкостенных труб. При этом были построены граничные кривые, позволяющие использовать методику МИКФ к решению и этой задачи. В статье [25] рассмотрена задача колебаний мембран в виде кругового сектора. Кроме того, МИКФ получил развитие при решении задачах предельного равновесия пластинок [44, 45, 48, 82].
В статьях [69, 70] изложены результаты исследований взаимосвязи максимального прогиба балок и пластинок с их основной частотой колебаний в ненагруженном состоянии. Оказалось, что все множество значений величины максимального прогиба пластинок с произвольными граничными условиями, нагруженных равномерно распределенной нагрузкой, функционально связаны с их основной частотой колебаний. График функции w0 – ω2 представляется единой кривой, которая объединяет все множество пластинок с выпуклым контуром и любыми комбинациями граничных условий. Эта закономерность носит фундаментальный характер в технической теории пластинок, поскольку позволяет по основной частоте колебаний находить максимальный прогиб пластинок и, наоборот, по максимальному прогибу – определять основную частоту колебаний. Эта закономерность имеет важное значение в области диагностики состояния и контроля качества строительных конструкций в виде пластинок.
Следует особо отметить работы, посвященные развитию и применению МИКФ к решению задач теории устойчивости пологих упругих оболочек [24, 27, 30, 31, 32]. Это перспективное направление, за исключением указанных работ, совершенно не проработано. Развивать его можно для решения задач поперечного изгиба и свободных колебаний оболочек.
Для составления программных расчетных комплексов с использованием коэффициента формы и методики МИКФ необходимо, как уже упоминалось, построение граничных кривых для пластинок не только с однородными, но и комбинированными граничными условиями. Поэтому эти задачи исследовались в многочисленных работах авторского коллектива Приокского государственного университета, развивающих рассматриваемое научное направление, В работах [33, …, 36, 81] строятся граничные кривые для задач колебаний пластинок, в статьях [37, …, 39, 81] – для задач поперечного изгиба пластинок.
В статьях [89, 90, 102] МИКФ получил развитие для решения задач поперечного изгиба треугольных и четырехугольных пластинок на упругом винклеровском основании и двухпараметрическом основании П.Л. Пастернака. При исследовании этой задачи возникла необходимость построения граничных аналитических зависимостей для вспомогательных величин, которые, как оказалось, тоже зависят только от коэффициента формы. В указанных публикациях проведены тщательные исследования по рациональному выбору геометрических преобразований заданных областей и функций, аппроксимирующих граничные кривые.
5. Применение МИКФ к расчету ортотропных пластинок
Возможность применения метода интерполяции по коэффициенту формы к расчету упругих ортотропных пластинок впервые упоминается в монографии В.И. Коробко [80]. В данной работе решение задачи об отыскании значения максимального прогиба упругой ортотропной пластинки в виде эллипса, жестко защемленного по контуру, приводится к изопериметрическому виду.
В статье [85] рассматриваются задачи о поперечном изгибе под действием равномерно распределенной нагрузки и о свободных колебаниях в ненагруженном состоянии треугольных пластинок из фанеры трех сортов (ФСФ из древесины березы, ФСФ из древесины лиственницы и бакелизированной фанеры марки ФБС), для решения которых используется аппарат метода интерполяции по коэффициенту формы. В первом приближении фанера рассматривается как ортотропный материал, при этом его упругие характеристики равномерно «размазаны» по толщине пластинок. В работе построены функциональные и графические зависимости для максимальных прогибов и частот собственных колебаний пластинок в виде равнобедренных треугольников из указанных материалов для случаев шарнирного опирания и жесткого защемления по контуру.
В работе [43] подходы, предложенные для треугольных пластинок, получили свое развитие к расчету по деформациям и к определению частот собственных колебаний прямоугольных пластинок из фанеры марок ФСФ и ФБС при однородных граничных условиях (шарнирное опирание или жесткое защемление вдоль всего контура). Полученные в работах [43, 85] функциональные зависимости могут быть использованы как для непосредственного расчета пластинок в виде прямоугольников и равнобедренных треугольников, так и в качестве опорных решений при расчете пластинок другой формы, например, трапецеидальных.
В статье [87] были построены функциональные зависимости для значений максимальных прогибов упругих ортотропных пластинок в виде правильных многоугольников для случаев однородных граничных условий (шарнирное опирание или жесткое защемление вдоль всего контура), а в статье [88] – для прямоугольных пластинок. В этих работах впервые было предложено при интерполяции между опорными решениями в качестве дополнительных аргументов (помимо коэффициента формы) использовать соотношения изгибных цилиндрических жесткостей пластинок (Dx/H, Dy/H). Такой подход позволил распространить возможности метода интерполяции по коэффициенту формы на более общий случай ортотропии:
Dx/H ∈ [0,2 … 5]; Dy/H ∈ [0,2 … 5].
Варьируя соотношениями цилиндрических жесткостей, были получены функциональные зависимости (граничные поверхности) для максимальных прогибов прямоугольных упругих ортотропных пластинок, находящихся под действием равномерно распределенной нагрузки, для случаев однородных и комбинированных (сочетание шарнирного опирания и жесткого защемления вдоль контура) граничных условий [91]. Приведенные в работе [91] выражения для граничных поверхностей максимальных прогибов заданы в виде полиномов третьей степени относительно двух переменных – соотношений цилиндрических жесткостей вдоль двух координатных осей. При этом неизвестные коэффициенты полиномов a…j зависят от коэффициента формы области и граничных условий на контуре и могут быть записаны в виде однотипных функций ψ(Kf). В работе приведены вычисленые значения коэффициентов A … H функций ψ(Kf) для всех возможных комбинаций жесткого защемления и шарнирного опирания по сторонам треугольных и четырехугольных пластинок.
Распространяя результаты, полученные в статье [85] для случая поперечного изгиба ортотропных пластинок в виде равнобедренных треугольников, на более общий случай ортотропии
(Dx/H ∈ [0,2 … 5]; Dy/H ∈ [0,2 … 5]),
в работе [95] были построены граничные поверхности максимальных прогибов таких пластинок. Выражения для этих поверхностей представляют собой произведение двух безразмерных функций f(Dx/H; Dy/H) и g(Kf) на размерный множитель q*A2/(H*Kf2). При этом все множество пластинок в виде равнобедренных треугольников было разделено на два подмножества в зависимости от угла α при основании:
α ∈ [20о, 60о) и α ∈ [60о, 75о].
В работе приведены значения коэффициентов функций f(Dx/H; Dy/H) и g(Kf) для всех возможных комбинаций шарнирного опирания и жесткого защемления по сторонам пластинок.
По аналогии с [91] в работе [97] построены функциональные зависимости для максимальных прогибов упругих ортотропных пластинок в виде ромбов, одна из осей ортотропии которых направлена вдоль стороны пластинки. Приведены значения коэффициентов A … H функций ψ(Kf) для всех возможных комбинаций жесткого защемления и шарнирного опирания по сторонам ромба. В работе также приводится пример решения тестовой задачи о поперечном изгибе ортотропной пластинки в виде параллелограмма, иллюстрирующий методику применения метода интерполяции по коэффициенту формы. В качестве опорных решений использовались значения, полученные по функциональным зависимостям для ромбов из данной работы и для прямоугольников из работы [91]. Результаты расчета верифицированы с помощью программно-вычислительного комплекса SCAD Office, реализующего метод конечных элементов (МКЭ).
В статье [98] выполнено построение граничных поверхностей максимальных прогибов для пластинок в виде ромбов, оси ортотропии которых проходят через вершины пластинки. При этом был использован подход, ранее нашедший отражение в работах [91, 97]. Полученные приближенные функциональные зависимости были верифицированы с помощью программно-вычислительного комплекса SCAD Office.
По результатам исследований [43, 85, 43, 87, 91, 95, 97] был разработан авторский программный комплекс, реализующий метод интерполяции по коэффициенту формы к расчету из условия жесткости упругих ортотропных пластинок ряда классов форм, имеющих наибольшее практическое значение (прямоугольники, треугольники, трапеции, параллелограммы и др.). Общий алгоритм и возможности вычислительного комплекса описаны в статье [98, 99].
Обобщением накопленных результатов исследований в области применения метода интерполяции по коэффициенту формы к расчету упругих ортотропных пластинок из условия жесткости можно считать работу [105], в которой подробно излагается методика решения задач с помощью МИКФ и приводятся тестовые примеры.
Дальнейшее развитие метода интерполяции по коэффициенту формы к расчету упругих ортотропных пластинок по деформациям связано с поиском наиболее оптимальных вариантов геометрического моделирования формы области пластинки и аппроксимирующих функций, используемых при интерполяции между опорными решениями. В этой связи следует отметить работу [107], в которой рассматривается расчет пластинок в виде параллелограммов. Для наиболее простого непрерывного геометрического преобразования, позволяющего получить параллелограмм из прямоугольника и ромба путем аффинного сдвига относительно одной из сторон, был предложен новый тип аппроксимирующей функции, учитывающей соотношение изгибных цилиндрических жесткостей вдоль сторон пластинки и условия опирания на контуре. В работе приведен тестовый пример с использованием известных ранее и новой аппроксимирующих функций, демонстрирующий более высокую точность результатов, полученных с использованием последней.
Учитывая подобие дифференциальных уравнений, описывающих поперечный изгиб и свободные колебания ортотропных пластинок, в статье [100] предлагается использовать аппарат метода интерполяции по коэффициенту формы для определения основной частоты собственных колебаний прямоугольных ортотропных пластинок. В работе выражения для граничных поверхностей основных частот собственных колебаний предлагается задавать в виде полиномов третьей степени относительно двух переменных – соотношений цилиндрических жесткостей вдоль двух координатных осей. Неизвестные коэффициенты полиномов a…j при этом являются функциями от коэффициента формы ψ(Kf) и зависят от граничных условий на контуре области. В статье приводятся значения коэффициентов A…H функций ψ(Kf) для всех возможных комбинаций жесткого защемления и шарнирного опирания по сторонам пластинок. Полученные функциональные зависимости могут быть использованы для непосредственного расчета прямоугольных пластинок, а также в качестве граничных поверхностей при выборе опорных решений.
Подход, изложенный в [100], был распространен на треугольные ортотропные пластинки [101]. В статье приводятся функциональные зависимости для основных частот собственных колебаний ортотропных пластинок в виде равнобедренных и прямоугольных треугольников. В первом случае одна из осей ортотропии направлена вдоль основания, во втором – вдоль катета треугольника. Так же как и в [100] выражения для граничных поверхностей основных частот собственных колебаний предлагается искать в виде полиномов третьей степени относительно двух переменных – соотношений цилиндрических жесткостей вдоль двух координатных осей. При этом неизвестные коэффициенты этих выражений также зависят от коэффициента формы и граничных условий. В работе приведено решение задачи о свободных колебаниях ортотропной пластинки в виде произвольного треугольника с использованием методики МИКФ.
В статье [106] изложена и проиллюстрирована тестовым примером методика применения метода интерполяции по коэффициенту формы к решению задачи о свободных колебаниях упругих ортотропных пластинок, обобщены результаты исследований, полученные в предыдущих работах, в частности, [100, 101]. Результаты вычислений, выполненных с помощью метода интерполяции по коэффициенту формы, верифицированы с использованием программного комплекса SCAD Office.
6. Метод интерполяции по отношению конформных радиусов (МИОКР)
Весьма перспективным при развитии геометрических методов является использование взамен коэффициента формы отношение конформных радиусов 
. Это отношение . используются при решении многих прикладных задач математической физики, гидро- и аэродинамики, магнитодинамики и др. [103]. В строительной механике впервые конформные радиусы в качестве обобщенного геометрического аргумента использовали В.И. Коробко и А.Н. Хусточкин для решения задач устойчивости пластинок [79] для получения односторонних оценок критического усилия пластинок при потере их устойчивости.
Исследования показали, что использование конформных радиусов отдельно как геометрических параметров области позволяет получать приемлемые результаты лишь для пластинок по форме, близких к правильной, прямоугольной и эллиптической. При этом необходимо учитывать масштаб и размеры пластинок, что значительно увеличивает трудоемкость расчета. Для преодоления этого недостатка в работе [79] и в последующих статьях [40, 108] была продолжена идея использования отношения конформных радиусов в качестве обобщенного геометрического аргумента при решении задачи устойчивости пластинок различных форм с выпуклым односвязным контуром.
В работе [76] было получено неравенство вида:
, (9)
где q0 – критическая сила при потере устойчивости;
K – числовой коэффициент, обращающий выражение (9) в равенство для круглых пластинок:
- при шарнирном опирании K = 5,783,
- при жестком защемлении K = 14,790);
D – цилиндрическая жесткость пластинки;
A – площадь пластинки;
ck – коэффициенты разложения отображающей функции в степенной ряд;
βk – отношение интегралов, вычисляемых через квадраты бесселевых функций.
Это неравенство дает асимптотически точные значения. Удерживая в разложении отображающей функции лишь первый член ряда, получается менее строгое выражение, которое позволяет получать приемлемые результаты лишь для пластинок по форме, близкой к правильной:
. (10)
В работах [40, 79, 108] был получен ряд новых результатов:
1. Оказалось, что для пластинок с однородными граничными условиями (либо шарнирное опирание по контуру, либо жесткое защемление) для множества пластинок в виде произвольных многоугольников, все стороны которых касаются вписанной окружности (включая все треугольники, правильные многоугольники и ромбы), критическая сила, соответствующая потере устойчивости пластинок, описывается одной аналитической зависимостью. Ни одна другая геометрическая характеристика не позволяет объединить значения критического усилия для такого большого подмножества форм пластинок одной аналитической зависимостью. Например пластинки из одного и того же материала в виде равнобедренного прямоугольного треугольника и ромба с углом 45,3о (для них отношение 
) равной площади имеют одинаковое значение критического усилия:
q0 = 24,674?
D/A – при шарнирном опирании;
q0 = 70,074?
D/A – при жестком защемлении.
2. На основе представления дифференциального уравнения устойчивости пластинок через комплексные переменные была установлена физико-математическая аналогия (в виде неравенства) критического усилия при потере устойчивости при равномерном всестороннем сжатии пластинок с отношением конформных радиусов. Эта позволило, не решая дифференциального уравнения устойчивости пластинок, а рассматривая лишь элементарную геометрическую задачу, связанную с анализом изменения отношения конформных радиусов, оценивать и качественную, и количественную стороны изменения критического усилия.
3. Область возможных значений критического усилия, как и в случае использования коэффициента формы, оказалась ограниченной с двух сторон: верхнюю границу дают решения для правильных многоугольных, треугольных и ромбических пластинок, а нижнюю – решения для эллиптических пластинок. Что позволяет исследовать рассматриваемую используя методику ИЗПМ или МИКФ.
4. Область возможных значений критического усилия, представленная в координатных осях q – 
, оказалась значительно (в 1,5 …2 раза) уже, чем при использовании коэффициента формы. Это позволяет получать оценки критического усилия во столько же раз с меньшей погрешностью, поскольку интервал, на котором осуществляется интерполяция, существенно сузился. В публикациях [92, 93, 94, 108. …, 117] приводятся многочисленные тестовые расчеты, подтверждающие этот вывод.
5. Установлена графически функциональная взаимосвязь отношения конформных радиусов с коэффициентом формы. На ее основе и теорем о коэффициенте формы сформулированы изопериметрические свойства и закономерности при различных геометрических преобразованиях отношения конформных радиусов для всего множества областей с выпуклым контуром. Эти свойства и закономерности представляют собой геометрическую основу метода интерполяции по отношению конформных радиусов.
С помощью МИОКР можно решать не только задачи устойчивости пластинок, но и задачи поперечного изгиба и колебаний пластинок. Это следует из математической аналогии дифференциальных уравнений эллиптического типа четвертого порядка, описывающих рассматриваемые задачи [18]:
(11)
где w(x,y) – функция прогибов пластинки в рассматриваемых задачах;
β2 – собственное значение дифференциального уравнения колебаний пластинок;
?2 – оператор Лапласа;
?2?2 – бигармонический оператор.
В работах [96, 115] математически доказано, что отношение конформных радиусов является геометрическим аналогом максимального прогиба, основной частоты колебаний и критического усилия:
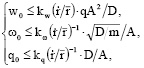(12)
где kw, kw, kq – константы, зависящие от вида граничных условий и обращающиеся в равенство выражения (12).
Из выражений (12) следует, что при заданных исходных данных пластинок и их граничных условий отношение конформных радиусов является единственным геометрическим аргументом, однозначно определяющим верхнюю оценку рассматриваемых интегральных ФМХ. Другими словами, отношение конформных радиусов является геометрическим аналогом этих ФМХ. Это означает, что, не решая дифференциальных уравнений (11), а рассматривая лишь элементарную геометрическую задачу, связанную с анализом изменения этого отношения при изменении геометрических параметров и формы пластинок, можно оценивать и качественную, и количественную стороны изменения рассматриваемых ФМХ.
В работе [41] рассматривалась задача определения основной частоты свободных колебаний пластинок с однородными граничными условиями. Для случаев шарнирного опирания пластинок по всему контуру и жесткого защемления построены граничные кривые в координатах «основная частота колебаний – отношение конформных радиусов». Эти кривые образуют область значений w в 2…2,5 раза уже, чем аналогичная область при использовании коэффициента формы. В последующих статьях [42, 84] на приведенных примерах показано, что использование отношения 
так же позволило получать решения для пластинок сложной формы с меньшей погрешностью, чем при использовании коэффициента формы. Такой же результат получен в задаче определения жесткости пластинок с однородными граничными условиями [47, 113].
В работах [94, 109, 110, 111, 116] построены аналитические и графические граничные зависимости, которые позволяют использовать методику МИКФ для решения задач поперечного изгиба пластинок с большей точностью. Задача по определению максимального прогиба пластинок различных форм с различными граничными условиями методом интерполяции по отношению конформных радиусов подробно рассмотрена в диссертации [114] и реализована в программном комплексе для ЭВМ [118].
К числу недостатков МИОКР можно отнести высокую сложность определения отношения 
для произвольных областей, поскольку общих формул для этого не существует. В работе [2] приводится прием нахождения этого отношения приближенными методами, один из таких приемов нахождения 
с помощью коэффициента формы приводится в статье [40].
Поскольку отношение конформных радиусов, как и коэффициент формы, позволяет моделировать геометрическую форму плоских областей, то другим направлением их применения является решение задач, связанных с определением рациональной геометрической формы пластинки, оболочки, или поперечного сечения стержня и ее оптимизация из условий прочности, жесткости и устойчивости при статических и динамических воздействиях. Первые исследования в этом направлении с использованием конформных радиусов выполнены в статье [112]. В ней рассматривается задача вариантного проектирования несущих панелей с опиранрием по контуру в виде лонжеронов и стрингеров, когда задано ограничение на величину максимального прогиба элементов заполнения такой панели в виде упругих пластинок. Путем геометрического моделирования формы области пластинок с помощью конформных радиусов и использованием геометрических методов строительной механики подбираются варианты заполнения несущей панели пластинками различных форм обладающих равной жесткостью.
Это направление исследований представляется перспективным [49], поскольку решение оптимизационных задач и задач, связанных с определением рациональной силовой схемы инженерных конструкций на начальных стадиях проектирования без привлечения сложных численных методов, является важной прикладной задачей.
Заключение
1. В представленном кратком обзоре:
– приведен анализ научных публикаций за последние 30 лет по проблеме – разработка, развитие и совершенствование инженерных методов решения двумерных задач теории упругости и строительной механики пластинок, в основу которых положены изопериметрические свойства интегральных геометрических характеристик односвязных областей с выпуклым контуром;
– сопоставлены возможности каждого из рассмотренных геометрических методов, обсуждены недостатки и положительные стороны каждого из них, показаны некоторые перспективные направления развития этих методов.
2. Рассматриваемые в обзоре интегральные геометрические характеристики (коэффициент формы области и отношение внутреннего к внешнему конформных радиусов), на основе изопериметрических свойств которых разрабатываются и развиваются геометрические методы решения двумерных задач теории упругости и строительной механики, являются количественной мерой симметрии любых односвязных областей с выпуклым контуром даже, если они не имеют осей симметрии. Следует отметить, что количественная оценка симметрии плоских областей, впервые в мировой науке предложена в работах авторского коллектива этого обзора.
3. Все рассмотренные в обзоре публикации относятся к проблеме решения задач, описываемых дифференциальными уравнениями эллиптического типа второго и четвертого порядков. Эти результаты носят междисциплинарный характер, многие из них могут найти самое широкое применение в математической физике для решения двумерных задач, описываемых дифференциальными уравнениями гиперболического и параболического типов, поскольку левые части этих уравнений аналогичны уравнениям эллиптического типа.
Библиографическая ссылка
Коробко В.И., Коробко А.В., Савин С.Ю., Черняев А.А. ОСНОВНЫЕ ЭТАПЫ РАЗВИТИЯ ГЕОМЕТРИЧЕСКИХ МЕТОДОВ РЕШЕНИЯ ДВУМЕРНЫХ ЗАДАЧ ТЕОРИИ УПРУГОСТИ И СТРОИТЕЛЬНОЙ МЕХАНИКИ ПЛАСТИНОК // Научное обозрение. Технические науки. – 2016. – № 3. – С. 54-69;URL: https://science-engineering.ru/ru/article/view?id=1088 (дата обращения: 23.11.2024).