Научный журнал

Научное обозрение. Технические науки

ISSN 2500-0799

ПИ №ФС77-57440

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Иванов Ю.М. 1 Семенов В.Г. 1 Осипенко К.В. 1

---

1 АО «МЕРА»

Стационарные подводные измерительные стенды, а также переносные системы магнитного поиска используют множество трехкомпонентных датчиков для измерения магнитного поля того или другого объекта на фоне магнитного поля Земли. Датчики должны измерять в одной и той же системе координат, называемой опорной. Между тем система координат каждого датчика отличается от опорной системы координат, что создает значительную погрешность измерения конечного результата. Многие годы эта погрешность считалась трудноустранимой. В 2002 году был разработан универсальный метод корректирующих матриц для значительного повышения точности измерения каждым датчиком. Метод корректирующих матриц не решил проблемы углового согласования датчиков, но подготовил почву для него. Недавно в дополнение к методу корректирующих матриц были разработаны два метода углового согласования трехкомпонентных датчиков. Один из них предназначен для бездемонтажной калибровки стационарных морских стендов, другой – для переносных систем магнитного поиска. Эти методы позволяют снизить погрешности от углового рассогласования в десятки раз.

Статья в формате PDF

0 KB

угловое согласование

дифференциальный магнитометр

погрешность измерения

1. Marshall B.J. Operational Aspects of Magnetic Measurement Ranges // Naval Forces 1989 v 10 N2. p 72–78.

2. Патент РФ № 2521134. Способ локализации источника магнитного поля дипольной модели, 2014.

3. Matthews D.C. Contemporary degaussing measuring ranges. Maritime Defence 1979 v 4 #12 p. 499–503.

4. Иванов Ю.М., Семенов В.Г. Корректирующие матрицы – путь к повышению точности трехкомпонентных магнитометров // Измерительная техника. – 2013. – №6. – С. 46–51.

5. Merrayo J.M.J. e.a. Scalar calibration of vector magnetometers // Meas. Sci. Technol. 2000. V.11. P.120–132.

6. Андре Анго. Математика для электро- и радиоинженеров. – М.: Наука, 1965. – С.18.

7. John J. Holmes. Exploitation of a Ship’s Magnetic Field Signatures. Morgan & Claypool. 2006. P.51.

В специальной магнитометрии, в отличие от обычной магнитометрии, применяются группы трехкомпонентных магнитометров, включенных по дифференциальной (разностной) схеме относительно опорного (компенсационного) магнитометра. Например, в проходных магнитоизмерительных стендах для измерения магнитных полей (МП) кораблей [1] (рис. 1) или в переносных системах магнитного поиска скрытых ферромагнитных объектов [2] (рис. 2). В таких стендах и системах показания всех магнитометров должны приводиться к единой системе координат (СК), например к СК опорного магнитометра.

Среди специалистов проблема углового согласования (УС) относительно опорной СК традиционно считалась трудноразрешимой, что неоднократно подчеркивалось в соответствующих публикациях, в частности:

– наименьшая погрешность установки датчиков на стенде водолазом по компасу составляет ±5о, тогда как требуемое УС датчика с опорной СК должно быть не хуже 35 угловых минут [1][1];

– стоимость геодезических и подводных работ по ориентации каждого трехкомпонентного датчика при установке на его штатном месте, составляет значительную часть стоимости затрат за весь срок службы магнитоизмерительного стенда 2-го поколения [3].

Отсюда следует, что угловая несогласованность датчиков является сильным источником систематической погрешности дифференциальных магнитометров.

Отметим, что для обычных трехкомпонентных магнитометров разработан универсальный метод резкого повышения точности за счет применения так называемых корректирующих матриц [4]. Но эффективное применение метода [4] к дифференциальным магнитометрам невозможно без соответствующего УС.

Далее в разделе 3 предлагается и рассматривается ряд перспективных методов УС.

Уравнение измерения разности магнитных индукций

В работе [4] результат измерения трехкомпонентным магнитометром представлен как искажение действительного значение вектора МИ некоторой 3х3 матрицей, называемой искажающей

Виi – Оi = ui·Bi = ui·si0 B0, (1)

где (Виi – Оi) – вектор-столбец результата измерения i-магнитометра, исправленный на его уходы нулей Оi; ui – искажающая матрица i-магнитометра в его собственной ортогональной СК (СОСКi); Bi – вектор-столбец действительного значения МИ в точке i в СОСКi. si0 – матрица ортогонального преобразования координат из некоторой опорной ортогональной ОСК0 в СОСКi; B0 – вектор-столбец действительного значения МИ в точке i в ОСК0.

Само понятие СОСК трехкомпонентного магнитометра введено ранее в работе [5]. СОСК жестко связана с магниточувствительными осями в общем случае неортогонального магнитометра и может быть определена для любого магнитометра, если известны неортогональности его осей.

Наиболее удобный, точный и помехоустойчивый метод определения неортогональностей, по которым строится искажающая матрица, разработан также в [4].

Если заранее определить искажающую матрицу i-магнитометра ui, а также матрицу si0, то последующие результаты измерения (1) можно просто и быстро корректировать либо в СОСКi либо в ОСК0

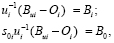(2)

где 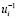– обратная искажающей или корректирующая матрица; si0 – транспонированная матрица УС.

С помощью (1) и (2) можно наглядно показать, как коррекция влияет на размер мульпликативных систематических погрешностей трехкомпонентного магнитометра

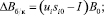
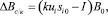(3)

где ΔBб/к, ΔBс/к – вектор-столбцы погрешностей магнитометра соответственно без коррекции и с коррекцией; 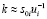– результат (неточно) определенных ортогональной матрицы si0 и искажающей ui.

Из (3) видно, чем точнее определены матрицы ui, и si0, тем ближе произведения ki ui si0 к единичной матрице I и тем меньше систематические погрешности магнитометра.

Как уже отмечалось выше, особенность магнитоизмерительных стендов, а также систем магнитного поиска [2] состоит в том, что там измеряют разности МИ между каждым измерительным и опорным (компенсационным) магнитометром, чтобы исключить влияние МП Земли (МПЗ), а также вариаций МПЗ, на результаты измерений МП объекта.

Учитывая эту специфику в соотношениях (2), составим типовое скорректированное уравнение измерения разности МИ объекта между измерительным i и компенсационным 0 трехкомпонентными датчиками.

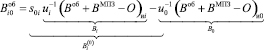, (4)

где 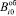– исправленная разность МИ объекта между точками i,0 в СОСК0; (…)иi, (…)и0 – результаты измерения соответствующим i-магнитометром и 0–магнитометром; 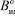, 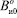– соответствующие части результатов измерения МП объекта в точках и 0; 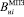, 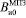– соответствующие части результатов измерения МПЗ в точках и 0; Bi, B0 – скорректированные результаты соответственно в СОСКi и СОСК0; 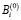– скорректированный результат точки i в СОСК0.

В уравнении (4) коррекцию выполняют корректирующие матрицы магнитометров и ортогональная матрица si0, которая осуществляет согласование СОСКi и СОСК0.

Корректирующие матрицы и уходы нулей определяются до установки магнитометров на штатных местах [4]. Разумеется, матрицу si0 следует определять после установки.

Методы определения матрицы УС

Предположим, что определение ортогональной матрицы si0 осуществляется в однородном МПЗ при отсутствии объекта (рис. 1). Как следует из (4), при удаленном объекте и синхронном измерении МПЗ в точках i и 0

,

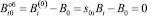то есть

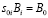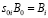или , (5)

где вектор-столбцы Bi, B0 известны в результате измерений и последующих коррекций; 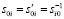, поскольку для ортогональной матрицы её транспонированная совпадает с обратной. Ниже используется правая часть соотношения (5). Каждому измерительному датчику i соответствует своя матрица УС si0.

Метод определения аргументов матрицы УС

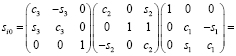
Искомую матрицу si0 можно выразить произведением элементарных матриц поворота. Например, поворотом на угол х1 вокруг орта 1, затем на угол х2 вокруг орта 2, затем на угол х3 вокруг орта 3 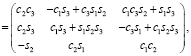[6]

(6)

где , .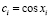

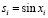То есть, (5) представляет собой систему трех нелинейных уравнений относительно трех неизвестных x1, x2, x3. Для решения нелинейных систем в пакете Матлаб разработана программа “fsolve”. Но для системы (5)+(6) программа неизменно выдавала физически неприемлемые значения углов (xa > 50, 50 = 0.087).

В этой связи опробован упрощенный аналог (6), учитывающий близость ci к единице и si к нулю

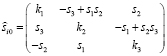, (7)

где .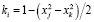

Кроме того, результаты решения систем зависели от выбора начальных данных х0. Поэтому целесообразно контролировать решения оценкой погрешности УС в виде

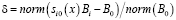. (8)

x = (x1 x2 x3) – результаты решения системы уравнений (5)+(7).

В качестве иллюстрации покажем весь процесс решения (5)-(8) на конкретном примере УС при:

B0 = (0.2097 0.0203 0.4945)·10–4, Bi = (0.22 0.02 0.49)·10–4;

x1 = 0.01, x2 = –0.02, x3 = 0.025.

Таблица 1

Решение систем (5)+(5) и (5)+(7)

Как видно из таблицы, точная система (5)+(6) дает физически неприемлемые решения (углы > 50), а «неточная» система (5)+(7) дает углы близкие к точным. Это оправдывает упрощение (7).Оценка (8) отслеживает точность решения для (5)+(7) и указывает на наиболее точное из полученных решений (выделено полужирным шрифтом):

x1 = 0.0101, x2 = –0.0199, x3 = 0.0252. (9)

Дальнейшее уточнение матрицы УС достигается подстановкой значений (9) в (6), при этом минимум оценки (8) снижается от 1.28e-04 до 9.45е-05.

Сравним погрешности УС (5)-(9) с вариантом без УС

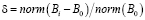. (10)

Таблица 2

Сравнение оценок погрешностей (8) и (10)

Таким образом, данные табл. 1 и 2 показывают, что метод (5)–(9) обеспечивает УС с достаточно высокой точностью.

Метод определения всей матрицы УС

Предположим, что в соотношении (5) скорректированные в СОСКi и СОСК0 результаты синхронного измерения однородного МПЗ, включая вариации МПЗ, составлены в виде прямоугольных матриц Сi, C0, 3×n, n = 3

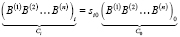(11)

Откуда по принципу наименьших квадратов предстаёт искомое решение относительно матрицы УС

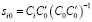, (12)

где 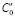– транспонированная матрица C0, n×3. Соответственно, произведение 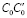образует квадратную матрицу 3×3.

Ожидается, что погрешность (12) должна зависеть от уровня вариаций МПЗ. Для проверки этой зависимости осуществлено компьютерное моделирование (12) в условиях примера к табл. 1, но при добавлении однородных шумов с нулевым средним и разными уровнями СКО, имитирующих короткопериодные вариаций МПЗ. Погрешность (12) оценивалась как сумма утроенной нормы СКО (12) и нормы среднего (12) (см. табл. 3).

Таблица 3

Погрешности (12) в зависимости от уровней СКО вариаций

Таблица 4

Зависимость погрешности УС по методу (14) от угла поворота

В литературе амплитуды короткопериодных вариаций МПЗ в спокойные периоды на широте Санкт-Петербурга оцениваются от долей до первых единиц нтл. То есть, СКО этих оценок были бы раза в три меньше.

Практически наблюдаемые значительно большие уровни вызваны индустриальными помехами, особенно от линии питания электротранспорта на постоянном токе. Но эти помехи неоднородные, то есть, они зависят от расстояний. Поэтому метод (12) может применяться в случае, если источники индустриальных помех значительны, но достаточно удалены, при этом расстояния между измерительными и опорным (компенсационным) датчиками достаточно малы.

Отметим, что ранее в монографии [6] описан аналог метода (12), посвященный компенсации вариаций МПЗ на магнитоизмерительном стенде. Вопросы и погрешности УС датчиков в [6] не рассматриваются, но делаются оптимистические выводы относительно практических возможностей компенсации вариаций.

Метод УС датчиков переносных систем магнитного поиска

Предположим, что система, схематически изображенная на рис. 2, находится вдали от объекта поиска в однородном МПЗ. Очевидно, что такая переносная система может подвергаться вспомогательным наклонам или поворотам на некоторые углы. Тогда по аналогии с выражением (5), запишем соотношение

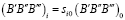, (13)

где 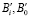– синхронные, скорректированные в соответствующей СОСК, результаты измерения МПЗ при вспомогательном повороте или наклоне всей системы вокруг её координатной оси х на некоторый угол; – то же самое вокруг оси y; 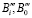– то же самое вокруг оси z.

Если угол поворота будет достаточно большим, то вектор-столбцы матрицы 3×3 в правой части будут некомпланарны. Тогда для неё существует обратная матрица, что определяет искомую матрицу УС

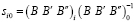. (14)

Погрешность УС по методу (14) зависит от угла поворота. Определим её с помощью компьютерного моделирования (14) при СКО вариаций МПЗ 10 нТл и СКО шумов датчиков 0.05 нТл, при прочих условиях по табл. 3.

Обсуждение результатов

В статье предложен и проанализирован ряд методов УС трехкомпонентных датчиков дифференциального магнитометра:

– метод определения углов матрицы УС или метод (5)-(9);

– метод определения всей матрицы УС или метод (12);

– метод вспомогательных поворотов системы поиска или метод (14).

Методы (5) и (12) предназначены для магнитоизмерительных стендов. Для систем магнитного поиска пригоден любой из трех.

Возможности метода (12) ограничены условием благоприятной помеховой обстановки.

Предложенные методы УС (5)–(9) и (14) в сочетании с методом корректирующих матриц [4] принципиально обеспечивают значительное повышение точности разнообразных трехкомпонентных систем специальной магнитометрии (см. табл. 2 и 4).

Библиографическая ссылка