Научный журнал

Научное обозрение. Технические науки

ISSN 2500-0799

ПИ №ФС77-57440

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Щипицын А.Г. 1

---

1 Национальный исследовательский Южно-Уральский государственный университет

Рассмотрена задача определения начальной ориентации стартующего с Земли объекта по информации, установленной на этом объекте бесплатформенной инерциальной навигационной системы. Использована априорная информация о векторе абсолютной угловой скорости Земли и векторе гравитационного ускорения начала связанной с объектом системы координат, а также использована информация, получаемая с трёх взаимно ортогональных датчиков угловой скорости и трёх взаимно ортогональных акселерометров. Применён подход использования двенадцати алгебраических уравнений относительно направляющих косинусов, шесть из которых выражают скалярный эквивалент условий векторного согласования измерительной и априорной информации, три – условия масштаба и ещё три – условия ортогональности для систем координат. Выполнены математические описания, составлены алгоритмы и разработаны программы определения направляющих косинусов от земной к объектной системе координат и имитационной модели этой процедуры с целью программного обеспечения бортового компьютера бесплатформенной инерциальной навигационной системы.

Статья в формате PDF

0 KB

стартующий с Земли объект

бесплатформенная инерциальная навигационная система

датчик угловой скорости

акселерометр

направляющие косинусы

математическое описание

алгоритм

программа

имитационная модель

1. Липтон А. Выставка инерциальных систем на подвижном основании. – М.: Наука, 1971. – 168 с.

2. Матвеев В.В., Распопов В.Я. Основы построения бесплатформенных инерциальных навигационных систем. – СПб.: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2009. – 280 с.

3. Щипицын А.Г. К задаче определения начальной ориентации объекта бесплатформенной инерциальной навигационной системой / А.Г. Щипицын, М.А. Щипицына, С.В. Слепова // XXV Российская школа по проблемам науки и технологий, посвященная 60-летию Победы. – Екатеринбург: УрО РАН, 2005. – С. 266–268.

4. Щипицына М.А. Математическая модель синтеза точности определения параметров начальной ориентации объекта бесплаформенной инерциальной навигационной системой // Сб. рефератов научно-исследовательских работ студентов по конкурсу грантов студентов, аспирантов и молодых ученых вузов Челябинской области. – Челябинск: Изд-во ЮУрГУ, 2007. – С. 152–153.

5. Щипицына М.А., Устюгов М.Н. Математическая модель для задачи определения параметров начальной ориентации объекта бесплатформенной инерциальной навигационной системой // Труды XXVI Российской школы по проблемам науки и технологий. – Екатеринбург: УрО РАН, 2006. – С. 241–243.

6. Щипицына М.А., Устюгов М.Н. Математическая модель для задачи синтеза точности начальной выставки бесплаформенной инерциальной навигационной системы // Сб. научн. тр. «Информационные системы и устройства». – Челябинск: Изд-во ЮУрГУ, 2007. – С. 102–108.

Указанная в заголовке статьи процедура в другой терминологии называется начальной выставкой навигационной системы [1, 2]. От точности начальной выставки системы зависит точность переменных навигационной информации объекта, так как процедурой начальной выставки определяются начальные условия, необходимые при интегрировании системы дифференциальных уравнений относительно таких переменных ориентации объекта, как направляющие косинусы от земной системы координат к объектной системе координат. Указанные начальные условия – это информация, которую необходимо иметь в бортовом компьютере до навигации объекта и которая может быть определена с использованием внешних по отношению к объекту источников информации, например с использованием информации с наземной навигационной системы, если она точнее системы, установленной на борту объекта. В данной работе, в отличие от задач, рассмотренных в работах [3–6], поставлена задача определения начальной ориентации объекта относительно Земли на основе информации бесплатформенной инерциальной навигационной системы этого же объекта, предполагая, что её точность является допустимой для начальных условий интегрирования указанной выше системы дифференциальных уравнений.

Постановка задачи

Объект, с которым связана система координат OYY1Y2Y3 (сокращённо: СКY), находится на Земле, с которой связана система координат OZZ1 Z2Z3 (сокращённо: СКZ), начало которой находится на поверхности Земли, ось OZZ1 направлена на восток, ось OZZ2 – на север, ось OZZ3 – по вертикали от центра сферической Земли с радиусом R и имеющей только собственное вращение с абсолютной постоянной угловой скоростью, величина которой равна u, а вектор направлен по оси вращения SN в сторону Северного полюса N. Гравитационное поле Земли полагаем сферическим с постоянным гравитационным ускорением, величина которого равна g в объёме объекта, а его вектор 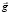направлен к центру Земли. Начало OZ СКZ находится на широте, определяемой углом φ.

Задача заключается в определении направляющих косинусов (НК) от СКZ к СКY вида

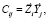i, j = 1, 2, 3 (1)

на основе имеющейся априорной информации о величинах u, R, g, φ и на основе измеряемой бесплатформенной инерциальной навигационной системой (БИНС) информации о трёх проекциях Ωj вектора 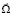абсолютной угловой объекта и трёх проекциях Aj вектора 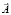кажущегося ускорения точки OY объекта, которую полагаем при рассматриваемой процедуре совпадающей с точкой OZ; 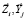– орты соответственно осей координат Zi, Yj. Кроме определения величин (1), необходимо указать условия существования и единственности решений поставленной задачи.

Математическое описание определения направляющих косинусов

Основой для решения поставленной задачи являются два векторных уравнения

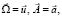(2)

где 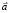– вектор кажущегося ускорения точки OZ, определяемый зависимостью

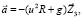(3)

где слагаемым u2R определено центростремительное ускорение точки OZ, вектор которого направлен противоположено орту 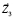. Согласно постановке задачи, векторы 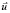, 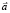определены проекциями в СКZ:

u1 = 0, u2 = ucosφ, u3 = usinφ;

a1 = 0, a2 = 0, a3 = – (u2R + g). (4)

Так как информация о векторах 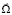, 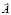поступает с БИНС, то эти векторы следует определить проекциями в СКY:

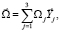
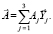(5)

Подставляя зависимости (5) в уравнения (3), умножая полученные равенства скалярно на орт 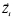и используя обозначения (1), получаем две системы уравнений относительно НК Cij по три уравнения в каждой:

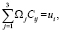i = 1, 2, 3, (6)

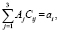i = 1, 2, 3. (7)

Из равенств (1) следуют зависимости между ортами:

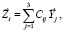i = 1, 2, 3. (8)

Умножая эти векторные равенства скалярно на орты 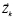и используя обозначения (1), получаем ещё две системы уравнений относительно НК Cij по три уравнения в каждой, выражающие соответственно условия масштаба и ортогональности для НК:

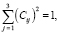i = 1, 2, 3, (9)

C11C21 + C12C22 + C13C23 = 0,

C11C31 + C12C32 + C13C33 = 0,

C21C31 + C22C32 + C23C23 = 0. (10)

Из системы (6) найдём

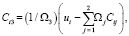i = 1, 2, 3. (11)

Подставив выражения (11) в уравнения (7), получим систему

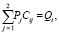i = 1, 2, 3, (12)

где введены обозначения

Pj = Aj – A3Ωj/Ω3, j = 1,2;

Qi = ai – A3ui/Ω3, i = 1, 2, 3. (13)

Из системы (12) найдём

Ci2 = pi – p0Ci1, i = 1, 2, 3. (14)

Подставив выражения (14) в зависимости (11), после несложных преобразований получим

Ci3 = ni + n0Ci1 , i = 1, 2, 3, (15)

где введены обозначения

p0 = P1/P2, pi = Qi/P2, n0 = [Ω2(P1/P2) – Ω1]/Ω3,

ni = [ui – (Ω2Qi/P2)]/Ω3, i = 1, 2, 3. (16)

Подставив выражения (14), (15) в уравнения (9), получим три квадратных уравнения относительно НК Ci1, i = 1, 2, 3:

Xi2 – 2P0iXi + Q0i = 0, i = 1, 2, 3. (17)

где обозначены неизвестные и коэффициенты этих уравнений:

Xi = Ci1, P0i = (p0p1 – n0ni)/(1 + p02 + n02), Q0i = = (pi2 + ni2 – 1)/(1 + p02 + n02), i = 1, 2, 3. (18)

Решая уравнения (17), получаем

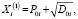
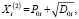i = 1, 2, 3. (19)

где введены обозначения:

D0i = P0i2 – Q0i, i = 1, 2, 3. (20)

Анализируя проделанные выкладки, можно указать на условия существования решения:

Ω3 ≠ 0, P2 ≠ 00

или с учётом выражения (13)

A2 – A3Ω2/Ω3 ≠ 0,

D0i = P0i2 – Q0i > 0, i = 1, 2, 3. (21)

Можно показать, что условия (21) выполняются, если векторы 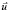, 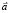ненулевые и неколлинеарны. То, что они ненулевые, очевидно. А требование их неколлинеарности означает, что рассматриваемая процедура начальной выставки не может быть реализована на полюсах Земли. Неоднозначность решения обусловлена наличием двух корней (20) уравнения (17), а единственность решения достигается проверкой выполнения условий ортогональности (10) для НК Cij для каждого из корней. Для этого найдём все НК, использовав решения (20) и выражения (14), (15):

Ci1(k) = Xi(k), Ci2(k) = ρi – ρ0Xi(k),

Ci3(k) = ηi + η0Xi(k), i = 1, 2, 3; k = 1, 2. (22)

Подставляя найденные решения (22) в уравнения (10) при k = 1, 2, находим тот индекс k, при котором эти уравнения обращаются в тождества, тем самым решаем вопрос о единственности решений.

Математическое описание имитационной модели начальной выставки

Выполненное выше математическое описание определения НК от земной СК к объектной СК основано на использовании измерений величин проекций Ωj, Aj, j = 1, 2, 3 датчиками БИНС объекта. Однако до использования БИНС следует иметь вычислительный алгоритм определения НК, который можно было бы инсталлировать в бортовой компьютер с гарантией, что этот алгоритм будет достоверно и достаточно точно вычислять требуемые НК на основе заданной априорной информации о величинах u, φ, R, g и указанной измеряемой информации Ωj, Aj, j = 1, 2, 3. Для обеспечения указанной гарантии достоверности и точности вычислений НК в бортовом компьютере необходимо построить имитационную модель измерений Ωj, Aj, j = 1, 2, 3 на основе заданной ориентации объекта относительно Земли.

Для построения указанной имитационной модели введём углы поворотов СКY относительно СКZ q1, q2, q3 в последовательности 1-2-3, то есть поворот на угол q1 выполнен вокруг оси Z1, поворот на угол q2 выполнен вокруг второй оси СК, получившейся после первого, поворот на угол q3 выполнен вокруг третьей оси СК, получившейся после второго поворота. Можно показать, что компоненты матриц НК, соответствующих отдельным указанным выше поворотам, имеют вид

S1101 = 1, S1201 = 0, S1301 = 0, S2101 = 0,

S2201 = cosq1, S2301 = –sinq1, S3101 = 0,

S3201 = sinq1, S3301 = cosq1; (23)

S1112 = cosq2, S1212 = 0, S1312 = sinq2, S2112 = 0,

S2212 = 1, S2312 = 0, S3112 = -sinq2, S3212 = 0,

S3312 = cosq2; (24)

S1123 = cosq3, S1223 = -sinq3, S1323 = 0,

S2123 = sinq3, S2223 = cosq1, S2323 = 0, S3123 = 0,

S3223 = 0, S3323 = 1. (25)

Использовав эти компоненты, найдём компоненты матрицы НК от СКZ к СКY:

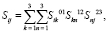i, j = 1, 2, 3. (26)

Далее определяем выражения для имитационных моделей измерений:

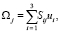
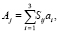j = 1, 2, 3, (27)

где проекции ui, ai определяются формулами (4). Используя величины (27) в описанной выше процедуре определения НК Сij и определив их, далее сравниваем полученные НК Сij с НК Sij, вычисляя модули разностей вида

ΔCij = |Cij – Sij|, i, j = 1, 2, 3. (28)

Заметим, что величины (28) можно рассматривать в качестве относительных погрешностей определяемых НК, так как наибольшая величина каждого НК не превышает единицы. А поэтому в качестве результирующей относительной погрешности всех девяти НК может быть принята величина

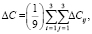(29)

которая может быть принята за меру вычислительной погрешности при определении НК и которая должна быть не больше заданной допустимой относительной погрешности ΔC* определения НК, то есть должна удовлетворять неравенству

ΔC ≤ ΔC*. (30)

Алгоритм имитационной модели определения направляющих косинусов

Выполненные выше математические описания позволяют сформулировать последовательность операций ввода исходной информации, вычислений и вывода результатов:

1. Задать:

u – модуль вектора абсолютной угловой скорости Земли;

g – модуль вектора гравитационного ускорения начала СКY;

R – радиус сферической Земли;

φ – широта начала СКY;

qk, k = 1, 2, 3 – углы ориентации СКY относительно СКZ;

ΔC* – допустимая относительная погрешность определения НК.

2. Вычислить ui, ai по формулам (4) и вычислить Sij по формулам (23)–(26).

3. Вычислить Ωj, Aj по формулам (27).

4. Вычислить Pj, Qi по формулам (13).

5. Вычислить p0, η0, ηi по формулам (16).

6. Вычислить P0i, Q0i по формулам (18).

7. Вычислить D0i по формулам (20).

8. Если Ω3 = 0 или P2 = 0 или D0i < 0, то вывести сообщение: «Не выполняется условие существования решения» и закончить алгоритм.

9. Вычислить Xi(k) по формулам (19).

10. Вычислить Ci1(k), Ci2(k), Ci3(k) по формулам (22).

11. Определить единственность решений подстановкой величин Ci1(k), Ci2(k), Ci3(k) в уравнения (10) при k = 1,2 и определения индекса k, при котором эти уравнения обращаются в тождества; в результате этой операции определить НК Cij.

12. Вычислить ΔCij по формулам (28).

13. Вычислить ΔC по формуле (29).

14. Проверить выполнение неравенства (30), и если оно не выполняется, то вывести сообщение: «Относительная погрешность вычисления НК Cij превышает допустимую» и закончить алгоритм.

15. Если алгоритм игнорирует пункты 8 и 14, то вывести величины Cij с сообщением: «Задача определения НК решена».

Исследование работы алгоритма имитационной модели заключается в анализе причин невыполнения условий существования решений (пункт 8) и неудовлетворения вычисленных НК допустимой относительной погрешности (пункт 14) для конкретных численных значений исходных данных. После выяснения этих причин и удаления из приведённого выше алгоритма пунктов 8 и 14 можно зафиксировать алгоритм определения НК для бортового компьютера БИНС, который будет включать в себя вычислительные операции пунктов с 3-го по 11-й, при замене пункта 3 формулировкой: «Измерить сигналы Ωj датчиков угловой скорости и сигналы Aj акселерометров БИНС».

О программе имитационной модели определения направляющих косинусов

На основе сформулированного выше алгоритма имитационной модели определения НК разработана программа, на вход которой подаётся исходная информация согласно пункту 0 алгоритма, а выходом которой являются вычисленные ГК, величина результирующей относительной погрешности вычисления НК, а также такие промежуточные результаты, как информация об удовлетворении условий существования решений, номер индекса k, при котором эти решения являются единственными. Разработанная программа имитационной модели определения направляющих косинусов позволяет анализировать влияние априорной информации о характеристиках местности (u, g, R φ) и исходной ориентации объекта относительно Земли (q1, q2, q3) на условия существования и единственности решений. Разработанная программа определения направляющих косинусов с учётом замечаний, сделанных после сформулированного алгоритма, и являющаяся частью указанной выше программы может быть использована для инсталляции её в бортовой компьютер БИНС.

Выводы

1. Для выполнения математического описания применён подход использования двенадцати алгебраических уравнений относительно направляющих косинусов, шесть из которых выражают скалярный эквивалент условий векторного согласования измерительной и априорной информации, три – условия масштаба и ещё три – условия ортогональности для систем координат.

2. Составлен алгоритм и разработана программа имитационной модели определения направляющих косинусов, которая может быть использована для программного обеспечения процедуры начальной выставки в бортовом компьютере бесплатформенной инерциальной навигационной системы.

Заключение

Применённый подход к выполнению математического описания может быть распространён на случай начальной выставки бесплатформенной инерциальной навигационной системы подвижного объекта, находящегося на борту подвижного носителя, на основе информации его навигационной системы.

Библиографическая ссылка