При моделировании фолдинга белка методом молекулярной динамики ограничения в производительности вычислительной системы являются одним из самых больших препятствий. Именно поэтому в данной области большое внимание уделяется оптимизации алгоритмов работы. Эта статья посвящена спискам Верле, как одному из вариантов оптимизации этапа поиска соседей.
Цель исследования: определить, насколько эффективно использование списков Верле для поиска соседей при проведении симуляции фолдинга белка.
Методы исследования:
– анализ существующих инструментов по моделированию фолдинга белка;
– практическое проведение симуляций фолдинга с анализом достигнутых результатов.
Результаты исследования и их обсуждение
На данный момент одним из самых распространенных пакетов ПО для проведения симуляций молекулярной динамики и, в частности, фолдинга белка является GROMACS [1]. Именно этот пакет был использован в данной статье для проведения симуляции.
Начиная с версии 4.6, GROMACS поддерживает две разных схемы по отсечению – оригинальную, основанную на группах частиц, и новую, использующую буфер Верле [2]. Между ними имеются серьезные различия, которые влияют на результаты, скорость работы и поддержку некоторых функций. Схему групп можно настроить так, что она будет работать почти как схема Верле, но ценой этого станет снижение производительности. Групповая схема особенно быстро работает при расчете молекул воды, которых очень много в широком круге симуляций, но на большинстве современных процессоров x86 схема Верле сполна компенсирует это преимущество лучшим параллелизмом при исполнении команд. Групповая схема считается устаревшей начиная с версии 5.0 и будет полностью удалена в будущих версиях [3].
В групповой схеме список соседей состоит из пар групп из по крайней мере одной частицы. Поначалу эти группы были группами зарядов, но при правильной обработке электростатических сил дальнего действия единственным преимуществом схемы становится производительность при проведении симуляций без буферизации. Пары групп помещаются в список соседей, если их геометрический центр находится в пределах радиуса отсечения. Взаимодействия между всеми частицами групп (по одной от каждой группы) рассчитываются для нескольких шагов симуляции, а затем список обновляется. Такой подход очень эффективен, поскольку в процессе поиска соседей проверяются расстояния только между группами зарядов, а не любыми парами частиц и ядра нековалентных сил могут быть оптимизированы, например, для «группы» молекул воды. Без явной буферизации применение схемы может привести к отклонениям в энергии системы из-за того, что некоторые пары частиц, находящиеся внутри радиуса отсечения взаимодействуют друг с другом, а некоторые частицы за радиусом отсечения, наоборот, взаимодействуют. Причиной может быть то, что частицы постоянно переходят через границу отсечения между шагами поиска соседей и/или, если группы состоят из более чем одной частицы, причиной могут быть частицы, выходящие или входящие в радиус отсечения, в то время как геометрический центр системы находится, напротив, в или вне радиуса.
Применение явного буфера в списке соседей позволит избавиться от этих ошибок, но значительно снизит производительность. Степень отклонений зависит от системы, свойств, которые необходимо изучить, и параметров отсечения.
Схема списков Верле по умолчанию использует буферизованные списки пар. В ней также используются кластеры частиц, но они не статические, как в групповой схеме. Напротив, эти кластеры определяются как область в пространстве и обычно состоят из 4–8 частиц. Такая группировка очень удобна при использовании потоковых вычислений, например SSE, AVX или CUDA на графических процессорах. На шагах, требующих проведения поиска соседей, создается список пар с буфером Верле, при этом радиус отсечения для списка пар больше, чем радиус отсечения взаимодействий. В ядрах нековалентных сил взаимодействия вычисляются только тогда, когда пара частиц находится в пределах радиуса отсечения в данный момент времени. Благодаря этому гарантируется, что при перемещении частиц рассчитываются силы почти между всеми частицами внутри радиуса отсечения. «Почти» все, потому что GROMACS обновляет списки пар с фиксированной частотой и скоростью. Пара частиц, находящихся за радиусом отсечения, теоретически может пройти достаточное расстояние за эти несколько шагов между обновлениями списков, чтобы оказаться внутри радиуса отсечения [4].
В результате имеется незначительный шанс потерь энергии, размер которых зависит от температуры. При использовании температурных связей размер буфера может быть определен автоматически, при заданном пороге потерь энергии.
Схема отсечения со списками Верле работает очень эффективно благодаря использованию кластеров частиц. В простейшем примере размер одного кластера – 4 частицы. Список пар затем собирается на основе пар кластеров. Поиск пар кластеров намного быстрее поиска пар частиц, поскольку 4*4 = 16 пар частиц добавляются в список за раз. После этого для расчетов множества частиц можно использовать одно и то же ядро нековалентных сил. Такой подход очень эффективен в сочетании с SIMD и SIMT элементами современной аппаратуры и позволяет одновременно исполнять множество операций с числами с плавающей запятой [5]. В большинстве вычислительных систем, особенно современных, такие ядра нековалентных сил намного быстрее обычных, используемых в групповой схеме.
В табл. 3 показаны примерные скорости симуляции при использовании разных схем. При симуляции произвольных групп атомов производительность будет примерно такая же, что и у модели tips3p. При моделировании белка в воде производительность будет чем-то средним между tip3p и tips3p.
Таблица 1
Примеры скоростей симуляции при разных схемах поиска соседей. Система Intel Core i7 2600, 3.4 GHz + Nvidia GTX660Ti
|
Система |
Групповая схема, без буфера |
Групповая схема, с буфером |
Схема Верле, с буфером |
Схема Верле, с буфером и ускорением ГП |
|
8 потоков MPI |
8 потоков MPI |
8 потоков OpenMP |
8 потоков OpenMP |
|
|
tip3p, с заряженными группами |
208 нс/день |
116 нс/день |
170 нс/день |
450 нс/день |
|
tips3p, с заряженными группами |
129 нс/день |
63 нс/день |
162 нс/день |
450 нс/день |
|
tips3p, без заряженных групп |
104 нс/день |
75 нс/день |
162 нс/день |
450 нс/день |
Проведение симуляции фолдинга белка
Данное исследование проводилось на ПК со следующими показателями:
- Процессор AMD Athlon II X4 620
- Видеокарта GeForce GTX 1050
В качестве белка был выбран один из самых коротких из существующих в мире белков – Trp-Cage (TC5b). Он также является белком, который сворачивается значительно быстрее других, что упрощает процесс симуляции.
Одним из главных препятствий при проведении симуляции являются проблемы с параллелизмом при симуляции [6]. Однако практически любой современный ПК имеет не только обычный ЦП, но и специализированный графический процессор. Графические процессоры обладают совершенно другой архитектурой, и параллельное выполнение простых вычислений является их главной целью. Выполнять вычисления можно как с помощью шейдеров и текстур, так и с помощью специализированного интерфейса – CUDA либо OpenCL. GROMACS поддерживает оба интерфейса. В данной работе вычисление проводилось на процессоре GeForce от NVIDIA. Обычно такие процессоры оптимизированы для интерфейса CUDA. CUDA широко используется при обработке изображений (например, [7]), но основной целью интерфейса является предоставление возможности выполнять сугубо математические вычисления на графическом процессоре, поэтому он часто используется и в задачах моделирования (например, [8]).
Проведенная симуляция обладала параметрами, указанными в табл. 1.
Важными результатами этой симуляции являются скорость – 1,716 ч/нс и коэффициент загруженности GPU/CPU. Коэффициент позволяет определить, насколько хорошо произошло распределение нагрузки между центральным и графическим процессором, и в идеале должен быть близким к 1. Результаты показаны в табл. 2.
Таблица 2
Параметры симуляции
|
Время |
12 нс (3M+3M) |
|
Шаг |
2 фс |
|
Ячейка |
куб со стороной 1 нм |
|
Модель воды |
явная, tip3p |
|
Алгоритм поиска соседей |
списки Верле |
|
Алгоритм расчета ограничений |
LINCS |
|
Алгоритм электростатического взаимодействия |
суммирование Эвальда |
|
Алгоритм расчета сил Ван дер Ваальса |
отсечение |
Стоит отметить, что, по сравнению с симуляциями, использующими неявную модель воды, скорость оказалась достаточно низкой. Однако преимущества неявной модели почти полностью сводятся на нет проблемами с декомпозицией домена и в итоге скорость оказывается почти одинаковой. К сожалению, GROMACS не позволяет использовать неявную модель в сочетании со списками Верле, а значит, и ускорение GPU оказывается невозможным. Использование GPU в сочетании с неявной моделью воды позволило бы на порядок ускорить процесс симуляции.
Таблица 3
Результаты симуляции
|
Достигнутая скорость |
1,716 ч/нс |
|
Загруженность GPU/CPU |
0,852 |
Для проверки точности симуляции использовался показатель RMSD (Root Mean-Square Deviation of atomic positions) – среднеквадратичное отклонение координат атомов или СКО. Отклонения измерялись в сравнении с координатами, полученными при помощи спектроскопии ядерного магнитного резонанса, которые может получить любой желающий из базы структур [9]. Использованный белок имел шифр 1l2y.
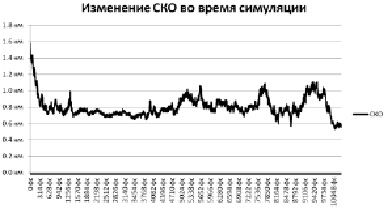
Рис. 1. СКО пятой симуляции
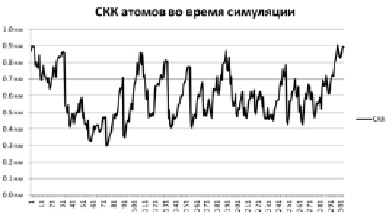
Рис. 2. СКК пятой симуляции
Отклонение от целевой структуры все уменьшается, скорее всего фолдинг белка проходит по верному пути. Первые пикасекунды симуляции характеризуются резким спадом отклонения в связи с тем, что исходная линейная структура белка начинает скручиваться. Также можно заметить резкие пики, в которые белок внезапно разворачивается и более или менее пологие участки, вероятно, соответствующие локальным минимумам энергии.
Также интерес представляет такой показатель, как RMSF (Root mean-square fluctuation) – среднеквадратичные колебания координат атома (СКК). По своей сути он очень похож на СКО с тем отличием, что СКО рассчитывается как среднее по всей системе, а СКК рассчитывается для одного атома в течение всей симуляции.
На рис. 3 показан график времени, затраченного на разные этапы симуляции молекулярной динамики. Явно видно, что основной проблемой является расчет сетки Эвальда (метод Эвальда используется для расчета сил электростатического взаимодействия).
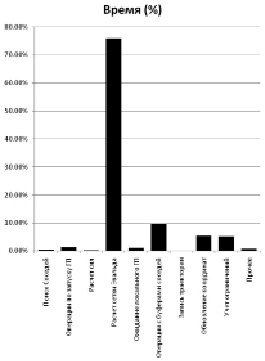
Рис. 3. Время, затраченное на разные группы операций в симуляции МД
Операции с буферами соседей заняли не больше 10 % времени – достаточно малая часть от всего времени выполнения, особенно по сравнению со временем, затраченным на расчет сетки Эвальда. Сам же поиск соседей и вовсе не потребовал сколько-нибудь значительных вычислительных мощностей.
Заключение
В GROMACS списки Верле позволяют эффективно использовать ГП для ускорения вычислений, что дает значительное преимущество над старой схемой. Они также являются более точным способом определения соседей. И, хотя групповая схема и может быть быстрее в силу своей простоты, на практике, при проведении симуляций, предпочтение нужно отдавать схеме Верле.
Библиографическая ссылка
Маслов Е.В., Белов Ю.С. ОПТИМИЗАЦИЯ ЗАДАЧИ МОДЕЛИРОВАНИЯ ФОЛДИНГА БЕЛКА МЕТОДАМИ МОЛЕКУЛЯРНОЙ ДИНАМИКИ С ИСПОЛЬЗОВАНИЕМ СПИСКОВ ВЕРЛЕ // Научное обозрение. Технические науки. 2018. № 4. С. 9-13;URL: https://science-engineering.ru/ru/article/view?id=1191 (дата обращения: 05.03.2026).


 science-review.ru
science-review.ru